
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неопределённый интеграл и его свойства.Содержание книги
Поиск на нашем сайте
Если функция F(x) – первообразная для функции f(x), то множество функций F(x)+C, где С – произвольная постоянная, называется неопределённым интегралом от функции f(x) и обозначается символом Свойства: 1. 2. 3. 4. 5.
Метод подстановки (неопределённый интеграл).
Вычисление неопределённого интеграла по частям.
Определённый интеграл и его свойства. Если существует конечный предел I интегральной суммы, то этот предел наз. определённым интегралом от функции f(x) по отрезку [a, b] и обозначается: Свойства: 1. по определению 2. по определению 3. каковы бы ни были числа a, b, c, всегда имеет место равенство 4. постоянный множитель можно выносить за знак определённого интеграла 5. определённый интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов
Формула Ньютона-Лейбница. Непосредственное интегрирование.
Метод подстановки (определённый интеграл).
Вычисление площадей плоских фигур.
x-y+2=0 y=0 x=-1 x=2 S -?
y=0
Vx -?
Вычисление пути, пройденного точкой.
t1=0c t2=10c
S -?
Задания для самоконтроля Контрольная работа (1 курс) Вариант 1
1. Представить в виде обыкновенной дроби: а) 0,(6) б) 1,(55) в) 0,1(2).
2. Упростить выражения: а)
3. Решить уравнения: а) | x-2|=1 б) | x-2| + |1-x| =3 в) г)
4. Решить неравенства: а) | 2x+6 | < 6 б) в)
5. Решить систему уравнений: а)
Вариант 2
1. Представить в виде обыкновенной дроби: а) 0,(11) б) 1,(5) в) 0,2(1).
2. Упростить выражения: а)
3. Решить уравнения: а) | x-1|=2 б) | x+2| + |1-x| =4 в) г)
4. Решить неравенства: а) | 3x+2 | < 5 б) в)
5. Решить систему уравнений: а)
Вариант 3. 1. Представить в виде обыкновенной дроби: а) 0,(8) б) 5,(1) в) 2,1(2).
2. Упростить выражения: а)
3. Решить уравнения: а) |2х+1|=5 б) | x+1| + |2-x| =4 в) г)
4. Решить неравенства: а) | 4-х| ≥3 б) в)
5. Решить систему уравнений: а)
Вариант 4. 1. Представить в виде обыкновенной дроби: а) 0,(7) б) 3,4(1) в) 2,(1).
2. Упростить выражения: а)
3. Решить уравнения: а) |4х-3|=8 б) | x+7| + |6-x| =1 в) г)
4. Решить неравенства: а) | 2-х| ≥5 б) в)
5. Решить систему уравнений: а)
Самостоятельная работа. Вариант 1. 1. Решить уравнения: а) 2. Решить систему уравнений методом Крамера: 3. Найти производные функций: а) 4. Построить график функции:
Вариант 2. 1. Решить уравнения: а) 2. Решить систему уравнений методом Крамера: 3. Найти производные функций: а) 4. Построить график функции: у=-2х3+15х2-36х+20
Вариант 3. 1. Решить уравнения: а) 2. Решить систему уравнений методом Крамера: 3. Найти производные функций: а) 4. Построить график функции: у=2х3-9х2+12х-2
Вариант 4. 1. Решить уравнения: а) 2. Решить систему уравнений методом Крамера: 3. Найти производные функций: а) 4. Построить график функции: у=х3-6х2+9х-3
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 483; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.72.189 (0.008 с.) |

 . При этом функция f(x) наз. подынтегральной функцией, f(x)dx – подынтегральным выражением, ф переменная x – переменной интегрирования. Интегрирование – операция, обратная дифференцированию.
. При этом функция f(x) наз. подынтегральной функцией, f(x)dx – подынтегральным выражением, ф переменная x – переменной интегрирования. Интегрирование – операция, обратная дифференцированию.
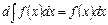


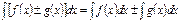 .
.





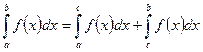







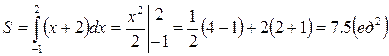
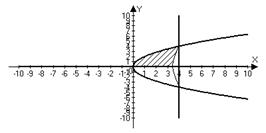 Вычисление объёмов тел вращения.
Вычисление объёмов тел вращения. y2=4x
y2=4x x=4
x=4
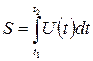
 U=3t2+2t+1(м/с)
U=3t2+2t+1(м/с)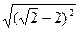 б) |
б) | 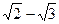 |
|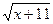 = х-1
= х-1


 б)
б) 
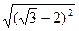 б) |√3-2|
б) |√3-2|
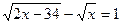
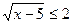

 б)
б) 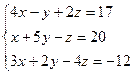
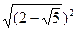 б) |√3-√2|
б) |√3-√2|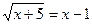
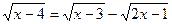
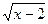 < 1
< 1 
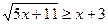
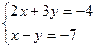 б)
б) 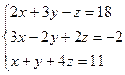
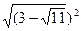 б) |√5-√7|
б) |√5-√7|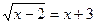
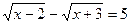
 < 2
< 2 
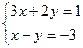 б)
б) 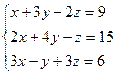
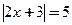 б)
б) 
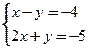
 б) у=(х3+6х-3)5
б) у=(х3+6х-3)5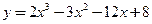
 б)
б) 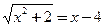

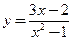 б)
б) 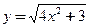
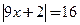 б)
б) 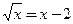

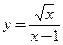 б) у=(2х5+4х-5)8
б) у=(2х5+4х-5)8 б)
б) 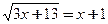
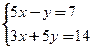
 б)
б) 



