
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1 действительные числаСодержание книги
Поиск на нашем сайте
Введение.
Цели и задачи дисциплины.
Учебная работа студента-заочника складывается из следующих основных элементов: проработка установочных и обзорных лекций, самостоятельного изучения программного материала по учебникам и учебным пособиям, решения задач, выполнения лабораторных работ и контрольных заданий. Поскольку основной формой обучения студента-заочника является самостоятельная работа по учебным материалам, то для обеспечения этой работы следует придерживаться следующих рекомендаций. 1. При изучении теоретического курса пользоваться каким-либо одним учебником или учебным пособием, чтобы не утрачивалась логическая связь между отдельными вопросами. Но если основное пособие не дает полного или ясного ответа на некоторые вопросы программы, необходимо обратиться к другим учебникам или пособиям. 2. При чтении учебника необходимо составлять конспект, в котором записываются формулы и решение типовых задач. 3. Приступая к решению задач по какому либо разделу, необходимо ознакомится по учебной литературе с соотношениями этого раздела. Внимательно прочитать условие задачи, обязательно (если это возможно) сделать рисунок, поясняющий сущность задачи.
Указания по оформлению контрольных заданий 1. Контрольные задания выполняются в обычной школьной тетради, на обложке которой приклеивается бланк, где указывается фамилия и инициалы студента, шифр специальности, номер зачётной книжки и номер контрольного задания. Вариант задания должен совпадать с последней цифрой номера зачётной книжки. Не рекомендуется выполнять два контрольных задания в одной тетради. 2. Условия задач в задании переписываются полностью без сокращений. Решение задач оформляется в соответствии с рекомендациями из методических указаний и примерами решения задач, приведенных в данном пособии перед каждой темой. После решения каждой задачи на страницах тетради оставляется место для замечаний преподавателя. 3. Если при рецензировании контрольное задание не зачтено, студент должен в этой же тетради провести работу над ошибками и представить ее на повторную рецензию. 4. Зачтенные контрольные задания предъявляются экзаменатору. Студент должен быть готов во время экзамена дать пояснения по существу решения задач, входящих в его контрольное задание.
Содержание дисциплины.
ВВЕДЕНИЕ Содержание учебного материала. Математика и научно-технический прогресс. Современная электронно- вычислительная техника и ее применение в реальной жизни. Роль математики в подготовке специалистов среднего звена (применительно к данной специальности).
ТАБЛИЦА ПРОИЗВОДНЫХ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Задания для самоконтроля Контрольная работа (1 курс) Вариант 1
1. Представить в виде обыкновенной дроби: а) 0,(6) б) 1,(55) в) 0,1(2).
2. Упростить выражения: а)
3. Решить уравнения: а) | x-2|=1 б) | x-2| + |1-x| =3 в) г)
4. Решить неравенства: а) | 2x+6 | < 6 б) в)
5. Решить систему уравнений: а)
Вариант 2
1. Представить в виде обыкновенной дроби: а) 0,(11) б) 1,(5) в) 0,2(1).
2. Упростить выражения: а)
3. Решить уравнения: а) | x-1|=2 б) | x+2| + |1-x| =4 в) г)
4. Решить неравенства: а) | 3x+2 | < 5 б) в)
5. Решить систему уравнений: а)
Вариант 3. 1. Представить в виде обыкновенной дроби: а) 0,(8) б) 5,(1) в) 2,1(2).
2. Упростить выражения: а)
3. Решить уравнения: а) |2х+1|=5 б) | x+1| + |2-x| =4 в) г)
4. Решить неравенства: а) | 4-х| ≥3 б) в)
5. Решить систему уравнений: а)
Вариант 4. 1. Представить в виде обыкновенной дроби: а) 0,(7) б) 3,4(1) в) 2,(1).
2. Упростить выражения: а)
3. Решить уравнения: а) |4х-3|=8 б) | x+7| + |6-x| =1 в) г)
4. Решить неравенства: а) | 2-х| ≥5 б) в)
5. Решить систему уравнений: а)
Самостоятельная работа. Вариант 1. 1. Решить уравнения: а) 2. Решить систему уравнений методом Крамера: 3. Найти производные функций: а) 4. Построить график функции:
Вариант 2. 1. Решить уравнения: а) 2. Решить систему уравнений методом Крамера: 3. Найти производные функций: а) 4. Построить график функции: у=-2х3+15х2-36х+20
Вариант 3. 1. Решить уравнения: а) 2. Решить систему уравнений методом Крамера: 3. Найти производные функций: а) 4. Построить график функции: у=2х3-9х2+12х-2
Вариант 4. 1. Решить уравнения: а) 2. Решить систему уравнений методом Крамера: 3. Найти производные функций: а) 4. Построить график функции: у=х3-6х2+9х-3
Итоговый тест по математике В номерах А1 – А10 указать правильный вариант ответа: А1. Упростить выражение: (5у0,7)3▪у-0,9. а) 125у3 б) 125у1,2 в) 15у1,2 г) 1252,8 А2. Найти длину вектора а)4 б) 1 в) 2 г) 1/2 А3. Найти значение выражения: а) -4 б) -2 в) -1 г) -1 + А4. Вычислить определитель: а) 44 б) -68 в) -44 г) 68 А5. Найти область определения функции: у = а) (- А6. Найти координаты вектора, проходящего через точки А(2,-1) и В(-3,8): а) (-5,9) б) (-1,7) в) (5,-7) г) (-5,7) А7. Решить уравнение: (0,7)4х = 0,49: а) 1/4 б) 1 в) 2 г) 1/2 А8. Решить неравенство: а) (0,3) б) (-3,+ А9. Найти объём пирамиды, если площадь её основания равна 3√2 м2, а высота √3 м: а) 3√6м3 б) √6м3 в) 18м3 г) 18√3м3 А10. Найти предел а) 0 б) 4 в) 8 г)
В номерах В1 – В3 записать правильный ответ: В1. Мальчик толкнул футбольный мяч, который после этого стал двигаться по закону S(t) = -0,5t2+6t, где S – пройденное мячом расстояние, измеряемое в метрах, а t – прошедшее после начала движения время, измеряемое в секундах. Через сколько секунд после начала движения мяч остановится? Ответ: _____________ В2. Найти целый корень уравнения 1 – sinx = cos2x. Ответ:______________ В3. Найти площадь фигуры, ограниченной линиями: у=2х2+1, у=1, х=3, х=6. Ответ:______________
Записать подробное решение номера С1 с обратной стороны листа. с1. При каких х выполняется неравенство
Задания для контрольных работ
ВАРИАНТ 1
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1) 2) ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 При каких размерах коробка (без крышки), изготовленная из квадратного листа картона, со стороной a, имеет наибольшую вместимость? ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: 1) y=6x-x2 и y=0. ВАРИАНТ 2
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1) 2)
ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Среди всех прямоугольников, имеющих данный периметр 2a, найти тот, площадь которого наибольшая. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2. Вычислить площади фигур, ограниченных линиями: y=x2+4x и x-y+4=0. ВАРИАНТ 3
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1. Исследовать на экстремум: 1) ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Кусок проволоки данной длины l согнуть в виде прямоугольника так, чтобы площадь последнего была наибольшей. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: 1) y=x3 и y=x. ВАРИАНТ 4
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1) ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Число 50 записать в виде суммы двух чисел, сумма кубов которых наименьшая. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: y=x3 и y=2x. ВАРИАНТ 5
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1)
ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Записать число 625 в виде произведения двух положительных чисел так, чтобы сумма их квадратов была наименьшая. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: y=2
ВАРИАНТ 6
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1)
ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Из всех прямоугольников, площадь которых равна 9 см2, найти прямоугольник с наименьшим периметром. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: y=2
ВАРИАНТ 7
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1) ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Из всех прямоугольных параллелепипедов, у которых в основании лежит квадрат и площадь полной поверхности равна 600 см2, найти параллелепипед наибольшего объема. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: 1) 3y=x2 и y= 3 ВАРИАНТ 8
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1)
ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Из всех прямоугольников с периметром P найти прямоугольник с наименьшей диагональю. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: 1) y=x2-3x и y=4-3x
ВАРИАНТ 9
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1) ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Из всех равнобедренных треугольников с периметром P найти треугольник с наибольшей площадью. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1)
ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: y=2x-x2 и y=x.
ВАРИАНТ 10
Тема 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ Найти производные функций: 1) 2) 3) 4) 5) 6) 7)
Тема 2. ПРИЛОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ЗАДАНИЕ № 1 Исследовать на экстремум: 1) ЗАДАНИЕ № 2 Найти наибольшее и наименьшее значения функции:
ЗАДАНИЕ № 3 Из всех прямоугольных треугольников, у которых сумма одного катета и гипотенузы равна l, найти треугольник с наибольшей площадью. ЗАДАНИЕ № 4 Найти точки перегиба функции:
ЗАДАНИЕ № 5 Найти асимптоты графика функции:
ЗАДАНИЕ № 6 Исследовать функцию и построить ее график:
Тема 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ ЗАДАНИЕ № 1 Вычислить интегралы: 1) ЗАДАНИЕ № 2 Вычислить площади фигур, ограниченных линиями: 1) Вопросы к зачёту.
1. Практические приемы вычислений с приближенными данными. 2. Линейные уравнения с одной переменной 3. Линейные неравенства с одной переменной 4. Квадратные уравнения. 5. Квадратные неравенства 6. Иррациональные уравнения 7. Иррациональные неравенства 8. Решение систем линейных уравнений 9. Решение систем линейных уравнений с двумя и тремя неизвестными с помощью определителей второго и третьего порядка 10. Предел числовой последовательности 11. Простейшие преобразования графиков функций. 12. Основные свойства предела. 13. Первый и второй замечательные пределы. 14. Преобразование и вычисление значений показательных выражений. 15. Преобразование и вычисление значений логарифмических выражений. 16. Построение графиков показательных функций 17. Построение графиков логарифмических функций 18. Построение графиков степенных функций 19. Показательные уравнения 20. Логарифмические уравнения 21. Показательные неравенства 22. Логарифмические неравенства
Вопросы к экзамену.
1. Синус, косинус, тангенс, котангенс числа. 2. Соотношения между тригонометрическими функциями одного аргумента 3.. Вычисление значений и тождественные преобразования тригонометрических выражений 4. Свойства и графики тригонометрических функций 5. Простейшие тригонометрические уравнения 6. Производная, ее геометрический и механический смысл 7. Производные суммы, произведения и частного двух функций. 8. Признаки возрастания и убывания функции 9. Применение производной к построению графиков функции 10. Наибольшее и наименьшее значения функции на промежутке. 11. Неопределенный интеграл и его свойства 12. Определенный интеграл и его геометрический смысл 13. Способы вычисления определенного интеграла. 14. Вычисление площадей плоских фигур с помощью определенного интеграла 15. Векторы на плоскости и в пространстве. 16. Формулы для вычисления длины вектора, угла между векторами, расстояния между двумя точками 17. Аксиомы стереометрии и простейшие следствия из них. 18. Многогранники. Призма. Параллелепипед и его свойства пирамида. 19. Тело вращения. Цилиндр и конус 20. Объемы и площади поверхностей геометрических тел
Список рекомендуемой литературы.
Основная литература: 1. Пехлецкий И.Д. Математика: учебник – М.: ИЦ «Академия», 2002 Гриф 2. Колмогоров А.Н. Алгебра и начала математического анализа 10-11 кл.: учебник – М.: «Просвещение», 2009 Гриф 3. Дадаян А.А. Математика: учебник – М.: «Форум», 2010 Гриф
Дополнительная литература:
1. Пехлецкий И.Д. Математика: Учебник для средних специальных учебных заведений. – М.: Академия, 2003. 2. Богомолов Н.В. Практические занятия по математике: Учебное пособие, 5-е изд. – М.: Высшая школа, 2002.
Введение.
Цели и задачи дисциплины.
Учебная работа студента-заочника складывается из следующих основных элементов: проработка установочных и обзорных лекций, самостоятельного изучения программного материала по учебникам и учебным пособиям, решения задач, выполнения лабораторных работ и контрольных заданий. Поскольку основной формой обучения студента-заочника является самостоятельная работа по учебным материалам, то для обеспечения этой работы следует придерживаться следующих рекомендаций. 1. При изучении теоретического курса пользоваться каким-либо одним учебником или учебным пособием, чтобы не утрачивалась логическая связь между отдельными вопросами. Но если основное пособие не дает полного или ясного ответа на некоторые вопросы программы, необходимо обратиться к другим учебникам или пособиям. 2. При чтении учебника необходимо составлять конспект, в котором записываются формулы и решение типовых задач. 3. Приступая к решению задач по какому либо разделу, необходимо ознакомится по учебной литературе с соотношениями этого раздела. Внимательно прочитать условие задачи, обязательно (если это возможно) сделать рисунок, поясняющий сущность задачи.
Указания по оформлению контрольных заданий 1. Контрольные задания выполняются в обычной школьной тетради, на обложке которой приклеивается бланк, где указывается фамилия и инициалы студента, шифр специальности, номер зачётной книжки и номер контрольного задания. Вариант задания должен совпадать с последней цифрой номера зачётной книжки. Не рекомендуется выполнять два контрольных задания в одной тетради. 2. Условия задач в задании переписываются полностью без сокращений. Решение задач оформляется в соответствии с рекомендациями из методических указаний и примерами решения задач, приведенных в данном пособии перед каждой темой. После решения каждой задачи на страницах тетради оставляется место для замечаний преподавателя. 3. Если при рецензировании контрольное задание не зачтено, студент должен в этой же тетради провести работу над ошибками и представить ее на повторную рецензию. 4. Зачтенные контрольные задания предъявляются экзаменатору. Студент должен быть готов во время экзамена дать пояснения по существу решения задач, входящих в его контрольное задание.
|

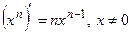
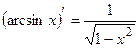

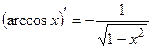

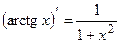
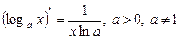
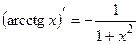

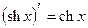


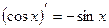
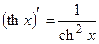
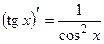

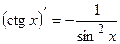
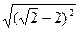 б) |
б) | 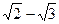 |
|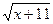 = х-1
= х-1


 б)
б) 
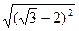 б) |√3-2|
б) |√3-2|
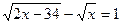
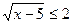

 б)
б) 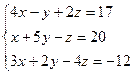
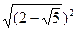 б) |√3-√2|
б) |√3-√2|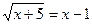
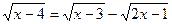
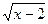 < 1
< 1 
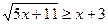
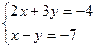 б)
б) 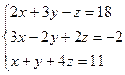
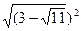 б) |√5-√7|
б) |√5-√7|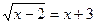
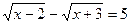
 < 2
< 2 
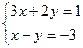 б)
б) 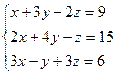
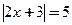 б)
б) 
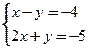
 б) у=(х3+6х-3)5
б) у=(х3+6х-3)5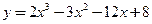
 б)
б) 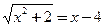

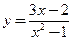 б)
б) 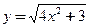
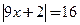 б)
б) 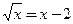

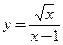 б) у=(2х5+4х-5)8
б) у=(2х5+4х-5)8 б)
б) 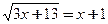
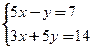
 б)
б) 
 , проходящего через точку А(1,-2):
, проходящего через точку А(1,-2): +
+ 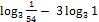
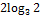
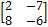 :
: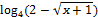
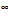 ;2) б) (-1,3) в) [-1,3) г) (-1,1)
;2) б) (-1,3) в) [-1,3) г) (-1,1)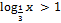 :
: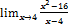 :
: .
.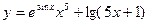
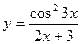
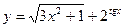




 ,
,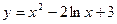 .
. на отрезке
на отрезке  .
.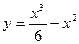 .
. .
. .
.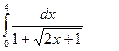 2)
2)  .
.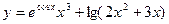
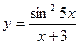
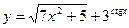


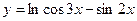
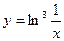
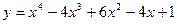 ,
,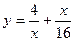 .
. на отрезке
на отрезке 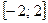 .
.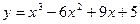 .
.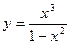 .
.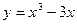 .
.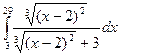 2)
2) 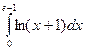 .
.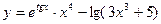
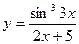
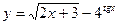
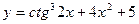
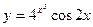
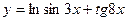

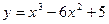 , 2)
, 2)  .
.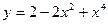 на отрезке
на отрезке  .
.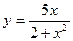 .
. .
.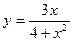 .
.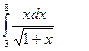 2)
2)  .
.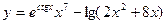
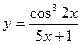

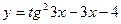
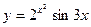
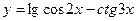
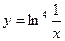
 , 2)
, 2)  .
.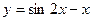 на отрезке
на отрезке  .
.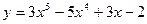 .
.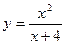
 .
.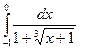 2)
2)  .
.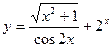
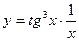
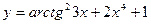
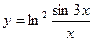
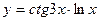
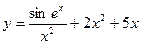

 , 2)
, 2)  .
.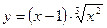 на отрезке
на отрезке 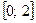 .
. .
.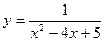 .
.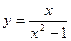 .
. 2)
2)  .
.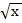 и y=x.
и y=x.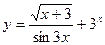
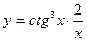
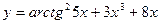
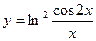
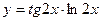

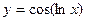
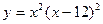 , 2)
, 2) 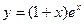 .
.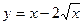 на отрезке
на отрезке  .
.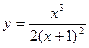 .
. 2)
2)  .
.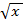 и
и  .
.


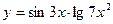

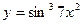
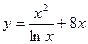
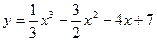 , 2)
, 2)  .
. на отрезке
на отрезке 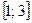 .
. .
.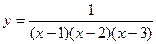 .
.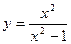 .
.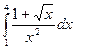 2)
2)  .
. .
.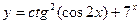
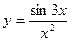
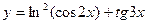

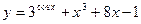
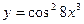
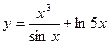
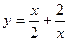 , 2)
, 2)  .
.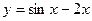 на отрезке
на отрезке  .
. .
.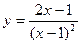 .
.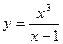 .
.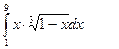 2)
2) 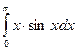 .
.
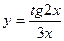


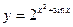
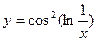

 , 2)
, 2)  .
.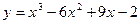 на отрезке
на отрезке 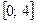 .
.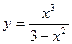 .
. 2)
2) 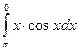 .
.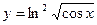
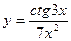

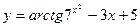
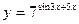
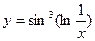
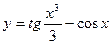
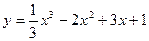 , 2)
, 2)  .
.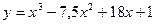 на отрезке
на отрезке  .
.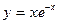 .
.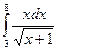 2)
2) 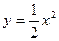 и y=4-x.
и y=4-x.


