
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б7 Уравнения, решаемые с помощью введения вспомогательного аргументСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
№1. №2.Существуют ли значения х, при которых выполняется равенство
№3 При каких значениях а уравнение
Анализируя результаты зачетной работы можно сделать вывод, что работа с учащимися по формированию осознанного и качественного умения решать тригонометрические уравнения прошла успешно. Об этом свидетельствуют: -улучшение результатов проверочных работ -отношение самих учащихся к проведённым занятиям. -школьники с интересом принимали участие в процессе обучения. Таким образом, цель эксперимента достигнута. Его результаты удовлетворительны. Данная методика имеет возможность применения на занятиях по алгебре и началам анализа в общеобразовательной школе.
Заключение
Таким образом, учитель сам обязан в достаточной мере владеть методиками формирования умений и навыков решать тригонометрические уравнения. С учётом того, что тригонометрические уравнения имеют несколько типов, то соответственно и методика для каждого типа различна. Бесспорно, достичь поставленной цели только с помощью средств и методов, предложенных авторами современных учебников, практически невозможно. Это связано с индивидуальными особенностями учащихся. Ведь в зависимости от уровня их базовых знаний по тригонометрии выстраивается линия возможностей изучения различных видов уравнений на разных уровнях. С решением уравнений, в которых переменная входит под знак одной или нескольких тригонометрических функций, так или иначе связаны многие задачи тригонометрии, стереометрии, физики и др. Процесс решения таких задач как бы синтезирует в себе практически все знания и умения, которые учащиеся приобретают при изучении элементов тригонометрии. Поэтому учитель сталкивается с довольно сложной проблемой выделения тех идей изучаемого материала, которые лежат в основе способов решения рассматриваемых задач, с целью их последующего обобщения и систематизации. Это важно и для осознанного усвоения учащимися теории, и для овладения некоторыми общими способами решения математических задач. Следует также заметить, что решение тригонометрических уравнений не только создает предпосылки для систематизации знаний учащихся, связанных с материалом тригонометрии. Например, свойства тригонометрических функций, приемы преобразования тригонометрических выражений и т.д. Но и дает возможность установить действенные связи с изученным алгебраическим материалом (уравнение, равносильность уравнений, виды алгебраических уравнений, способы их решения, приемы преобразования алгебраических выражений и т.п.). В этом состоит одна из особенностей материала, связанная с изучением тригонометрических уравнений.
Другая особенность – в исключительном разнообразии таких уравнений. Именно это разнообразие влечет определенные трудности в их классификации; его следствием могут быть и затруднения в решении тригонометрических уравнений, в частности, - в выборе того приема, который целесообразно применить для получения искомого множества значений переменной. Указанные особенности должны быть учтены учителем при разработке методики обучения школьников решению тригонометрических уравнений. Тригонометрические уравнения занимают достойное место в процессе обучения математики и развитии личности в целом.
Литература 1. 2. Адрова И.А., Ромашко И.В. Модульный урок в X классе по теме «Решение тригонометрических уравнений» //Математика в школе. 2001. №4. С. 28-32. 3. Галанов Ю.И., Некряч Е.Н., Рожкова В.И. Тригонометрические уравнения. Электронное пособие для абитуриентов.- Издательство Томского политехнического университета.2011. 4. Гилемханов Р.Г. Освободимся от лишней работы (при решении однородных тригонометрических уравнений) //Математика в школе. 2000. № 10. С.9 5. Зандер В.К. О блочном изучении математики / на примере изучения темы «Решение тригонометрических уравнений и неравенств» //Математика в школе.1991. № 4, С.38-42. 6. Звавич В.И., Пигарев Б.П. Тригонометрические уравнения //Математика в школе. 1995. № 2. С.23-33
7. Звавич В.И., Пигарев Б.П. Тригонометрические уравнения (решение уравнений + варианты самостоятельных работ) //Математика в школе. № 3, С.18-27. 8. Золотухин Е.П. Замечания о решении уравнений вида asinx+bcosx=c //Математика в школе. 1991. № 3. С.84. 9. Калинин А.К. О решении тригонометрических неравенств. // Математика. Приложение к газете «Первое сентября» № 6, 1991г. 10. Клещев В.А. Обобщение метода интервалов на тригонометрической окружности //Математика в школе. 1992. № 6. С. 17-18. 11. Мирошин В. Отбор корней в тригонометрических уравнениях.// Математика. Приложение к газете «Первое сентября» № 17, 2006г. 12. Мордкович А.Г. Алгебра и начала анализа. 10-11 кл.: Учебник для общеобразовательных учреждений. – М.: Мнемозина, 2010. – 336с.:ил. 13. Орлова Т. Решение однородных тригонометрических уравнений: Конкурс “Я иду на урок” //Математика. Приложение к газете «Первое сентября» № 48, 1999г. 14. Пичурин Л.Ф. О тригонометрии и не только о ней: М. Просвещение, 1985г. 15. Решетников Н.Н. Тригонометрия в школе: М. Педагогический университет «Первое сентября», 2006, лк 1. 16. Смоляков А.Н., Севрюков П.Ф. Приемы решения тригонометрических уравнений //Математика в школе. 2004. № 1. С. 24-26. 17. Суворова М.В. Повторительно-обобщающие уроки в курсе математики (на примере изучения темы «Тригонометрические уравнения» //Математика в школе. 1995. № 4. С.12-13 18. Токарева А. Тригонометрические неравенства. // Математика. // Приложение к газете «Первое сентября» № 44, 2002 г. 19. Шабунин М. Тригонометрические уравнения. // Математика. Приложение к газете «Первое сентября» № 12,13, 1995г. 20. Филатов В.Г. О потере корней при решении тригонометрических уравнений //Математика в школе. 1991. №2. С.57-59. 21. Черкасов О.Ю. Математика: интенсивный курс подготовки к экзамену/Олег Черкасов, Андрей Якушев. – 11-еизд. – М.; Айрис-пресс,2006.-448 с.; ил.-(Домашний репетитор). 22. Шабашова О.В. Приемы отбора корней в тригонометрических уравнениях //Математика в школе. 2004. №1. С.20-24.
Приложение 1 Конспект урока, направленного на формирование умений решать тригонометрические уравнения. В начале урока учитель предлагает ученикам вспомнить уже известные методы решения тригонометрических уравнений. Для этого ученики должны устно предложить метод решения для каждого из 5 уравнений. Все основные узлы решений учитель записывает на доске под диктовку учеников, дополняя или исправляя их объяснения. Имеет смысл на первых примерах задействовать не сильных учеников, чтобы они включились в работу и активно помогали при выведении формул. Далее представлена таблица с разбором возможных решений. После каждого решения, полностью проговаривается идея метода учениками с поправками учителя.
Переход к основной части Данный этап урока, призван сформировать проблему, решению которой будет посвящена основная часть урока.
Основная часть После получения серии корней в части 2.1 учитель обращает внимание некоторую «некомпактность» данного ответа и сложности в восприятии этой информации. Например, сложности, которые возникнут, если необходимо будет найти корни на заданном промежутке. Далее учитель сообщает, что одно из замечательных отличий тригонометрических уравнений состоит в том, что в зависимости от избранного метода решения, можно получить разные виды записи одних и тех же корней. Поэтому, возможно, если мы решим данное в 2.1 уравнение каким-то другим способом, вариант записи ответа получится предпочтительнее.
Закрепление материала
Цель данного этапа проверить действие формул на практике. Учитель совместно с учениками на доске оформляет решение. Ученики записывают решение в тетрадь.
Проверка знаний Цель данного этапа получить обратную связь от учащихся. Увидеть насколько они поняли суть метода и насколько они научились его применять, чтобы понять какой будет следующий урок.
Итог урока Учитель поздравляет учеников с тем, что они узнали ещё один способ решения тригонометрических уравнений, ещё раз повторяет алгоритм его применения. После чего предлагает учащимся попытаться решить следующее уравнение различными способами:
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 601; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.137.175 (0.011 с.) |

 ; (
; (
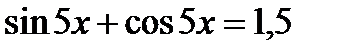 ? (нет)
? (нет) не имеет решений? (а<-
не имеет решений? (а<- 

 С помощью теоремы обратной теореме Виета находим:
С помощью теоремы обратной теореме Виета находим:
 По условию остаётся только один корень. Производим обратную замену:
По условию остаётся только один корень. Производим обратную замену:
 На доске появляется координатная окружность. С помощью координатной окружности, ещё раз проговаривая как её использовать, находим значения корней:
На доске появляется координатная окружность. С помощью координатной окружности, ещё раз проговаривая как её использовать, находим значения корней:

 надо заметить, что в этом случае мы совершаем не равносильное преобразование и рискуем потерять серию корней, что недопустимо. Поэтому имеет смысл решать это уравнение иначе. Ученики должны догадаться, что самый простой способ – разложение на множители:
надо заметить, что в этом случае мы совершаем не равносильное преобразование и рискуем потерять серию корней, что недопустимо. Поэтому имеет смысл решать это уравнение иначе. Ученики должны догадаться, что самый простой способ – разложение на множители:
 Ученики проговаривают критерий: «Произведение равно 0 тогда и только тогда, когда один из множителей равен 0, а другой при этом не теряет смысла»
Ученики проговаривают критерий: «Произведение равно 0 тогда и только тогда, когда один из множителей равен 0, а другой при этом не теряет смысла»
 На экране появляется тригонометрическая окружность, с помощью которой ученики находят серии корней:
На экране появляется тригонометрическая окружность, с помощью которой ученики находят серии корней:

 Появляется тригонометрическая окружность, с помощью которой, учащиеся находят серии корней:
Появляется тригонометрическая окружность, с помощью которой, учащиеся находят серии корней:

 . И сводится к квадратному уравнению относительно тангенса:
. И сводится к квадратному уравнению относительно тангенса:
 Так как такой тип уравнений уже повторялся, то возможно, сообщив об этом ученикам, перейти к следующему уравнению. Однако, можно решить данное уравнение до конца. Корни, в этом случае, предпочтительно находить через теорему обратную теореме Виета.
Так как такой тип уравнений уже повторялся, то возможно, сообщив об этом ученикам, перейти к следующему уравнению. Однако, можно решить данное уравнение до конца. Корни, в этом случае, предпочтительно находить через теорему обратную теореме Виета.
 (проговаривается, что данное выражение не будет равно 0, так как в противном случае получаем противоречие основному тригонометрическому тождеству). К доске вызывается ученик, который будет оформлять решение, остальные самостоятельно оформляют решение в тетради, а затем проверяют. Возможное решение:
(проговаривается, что данное выражение не будет равно 0, так как в противном случае получаем противоречие основному тригонометрическому тождеству). К доске вызывается ученик, который будет оформлять решение, остальные самостоятельно оформляют решение в тетради, а затем проверяют. Возможное решение:

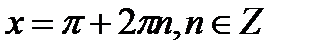 Корнем уравнения. И если да, то должны включить эту серию в ответ. Всё это несколько осложняет использование формул.
Корнем уравнения. И если да, то должны включить эту серию в ответ. Всё это несколько осложняет использование формул.
 делать не надо, так как тангенс половинного угла присутствует, и во время замены мы не сузим область допустимых значений.
делать не надо, так как тангенс половинного угла присутствует, и во время замены мы не сузим область допустимых значений.
 Критерий равенства произведения 0, проговаривается
Критерий равенства произведения 0, проговаривается
 или
или  Второе уравнение не имеет корней, остаётся единственная серия:
Второе уравнение не имеет корней, остаётся единственная серия:

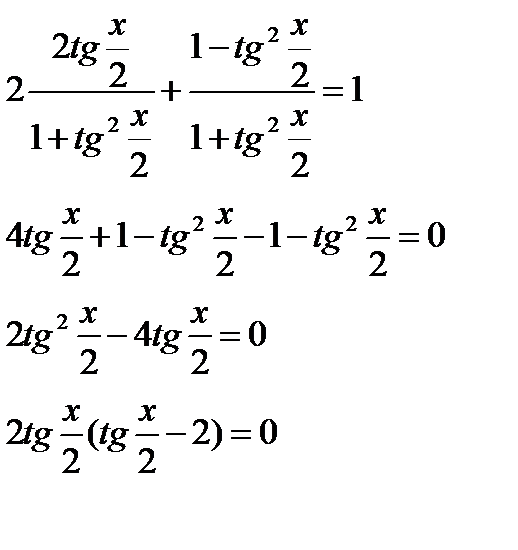 Критерий равенства произведения 0, проговаривается
Критерий равенства произведения 0, проговаривается
 или
или  Отсюда получаем серии корней:
Отсюда получаем серии корней:
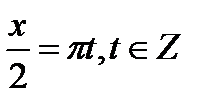 или
или  Итого ответ:
Итого ответ:
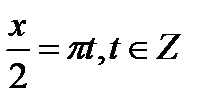
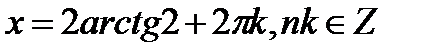
 Критерий равенства произведения 0, проговаривается. Отсюда:
Критерий равенства произведения 0, проговаривается. Отсюда:
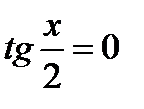 или
или  Решая второе уравнение с помощью дискриминанта, и используя нечетность тангенса, получаем следующие серии корней:
Решая второе уравнение с помощью дискриминанта, и используя нечетность тангенса, получаем следующие серии корней:
 Отсюда:
Отсюда:
 После того как ученики решают уравнение, учитель выясняет сколько учеников успешно справилось с решением и если ребята ошиблись, то где они допустили ошибку.
После того как ученики решают уравнение, учитель выясняет сколько учеников успешно справилось с решением и если ребята ошиблись, то где они допустили ошибку.




