
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды простейших тригонометрических уравнений и методы их решенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Необходимость классификации уравнений вызывается невозможностью найти общий метод их решения. Очевидно, что классифицировать тригонометрические уравнения имеет смысл с опорой на методы их решения. Мы будем рассматривать типы уравнений в той последовательности, которая представляется нам наиболее приемлемой для обучения школьников, то есть в последовательности, построенной в соответствии с принципом «от простого к сложному». Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим. К простейшим тригонометрическим уравнениям относятся уравнения вида: На эти уравнения следует обратить особое внимание, так как без умения их решать невозможно решить никакое другое тригонометрическое уравнение. Лучше всего, если учащиеся будут иметь схемы решения каждого из простейших уравнений
Если Если Особые случаи:
Любая из этих формул может быть заменена формулой общего вида, однако они проще и их выгоднее применять при решении уравнений. Полезно помнить, что при
Уравнение вида Если Если Особые случаи:
Нужно помнить, что при
Уравнение вида
Нужно помнить, что при
Уравнение вида
Нужно помнить, что при
Уравнения, сводящиеся к простейшим, имеют вид Данные уравнения также являются простейшими и решаются сначала относительно f(x), а затем полученные уравнения решаются относительно х. Примеры: 1.
2.
3.
2.2.1 Уравнения, являющиеся равенством двух одноимённых тригонометрических функций: а) уравнения вида
б) уравнения вида
в) уравнения вида
Примеры: Решите уравнение:
2. Решите уравнение:
Тригонометрические уравнения, содержащие одну и ту же функцию одного и того же аргумента и решаемые методом подстановки Уравнения данного вида Пример: Решите уравнение:
Пусть
Оба корня уравнения удовлетворяют условию допустимого значения t, следовательно, переходим к обратной замене.
Однородные уравнения Предварительно можно показать учащимся вид однородной функции от двух переменных U и V первой степени, например, 3U + 2V; второй степени: Для лучшего усвоения и закрепления идеи необходимо решить с учащимися следующее уравнение: Обозначим Получается однородное уравнение второй степени:
Имеем 2 случая: U = V или V = 0,5 U
Как правило, на практике очень часто встречается Примеры: 1. Это однородное уравнение первой степени. Обе части уравнения нужно разделить на cosx. При этом получится равносильное уравнение. Чтобы в этом удостовериться, покажем, что уравнение cosx = 0 не содержит корней данного уравнения. Действительно, если
, то
Но это невозможно, т.к. Следовательно, имеем равносильное уравнение
2. Это однородное уравнение второй степени. Получим равносильное уравнение после деления обеих частей уравнения на
При решении уравнений такого типа необходимо пользоваться известным правилом: произведение нескольких множителей равно нулю, если хотя бы один из них равен нулю, а остальные при этом имеют смысл. Примеры: 1.
2. Сгруппировав соответствующие слагаемые, получим:
Один из способов решения такого уравнения состоит в том, что левую часть уравнения можно преобразовать по формуле:
Примеры:
1.
Подставляя в формулу, получаем:
2.
Подставляя в формулу, получаем
К сожалению, внимание учащихся нечасто обращается на преобразование выражения В некоторых пособиях эта формула приведена в таком виде
Такая запись приведёт к ошибке, если, например, a и b отрицательны.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 786; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.178.220 (0.009 с.) |

 ,
,  ,
,  ,
,  .
. Уравнение вида
Уравнение вида  , то
, то 
 , то
, то  (рис 1, а)
(рис 1, а) ;
; 
 ;
; 
 ;
; 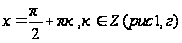

 ;
;  ;
; .
. .
. (рис 1, д)
(рис 1, д) ;
; 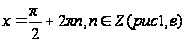
 ;
; 
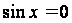 ;
; 
 ;
;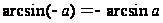 ;
; .
. .
. (рис 1, и)
(рис 1, и) ;
; 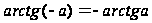 ;
;
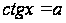 .
. (рис 1, к)
(рис 1, к) ;
;  ;
; ;
; 
 ,
,  ,
,  ,
,  .
. ;
;




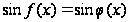 равносильно совокупности уравнений:
равносильно совокупности уравнений:
 равносильно совокупности уравнений:
равносильно совокупности уравнений:
 равносильно системе уравнений:
равносильно системе уравнений: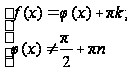


 , где
, где  тригонометрическая функция часто называются сводящимися к квадратным и решаются методом подстановки вместо тригонометрической функции данного аргумента некоторого параметра t с учётом допустимых значений t в зависимости от области значения функции.
тригонометрическая функция часто называются сводящимися к квадратным и решаются методом подстановки вместо тригонометрической функции данного аргумента некоторого параметра t с учётом допустимых значений t в зависимости от области значения функции.
 тогда уравнение примет вид:
тогда уравнение примет вид:
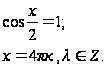
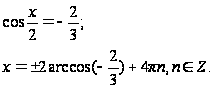

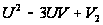 ; третьей степени:
; третьей степени:  и т.д., сформировав понятия выражения, однородного относительно переменных U и V.
и т.д., сформировав понятия выражения, однородного относительно переменных U и V. .
.
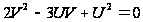 ;
;
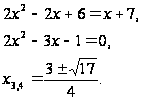
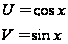 .
. .
.
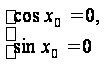
 .
.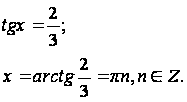
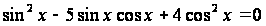 .
. .
.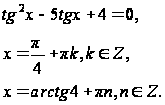

 или
или 

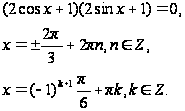




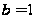 ;
;
 , т.к. это решение системы
, т.к. это решение системы 




 , т.к. это решение системы
, т.к. это решение системы 

 .
. где
где 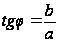 .
.


