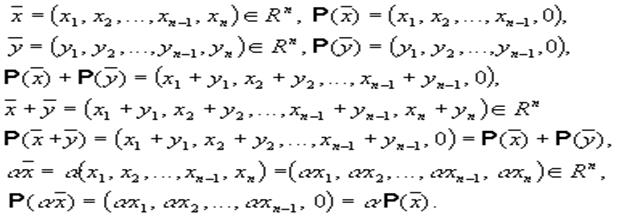Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие уравнения прямой, как линии пересечения двух плоскостейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой. Вообще любые две не параллельные плоскости, заданные общими уравнениями
определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой Билет 6 Записать выражение для угла между прямой и плоскостью, условие параллельности и перпендикулярности прямой и плоскости. Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямами плоскость заданы уравнениями
Если угол между векторами Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы
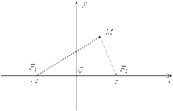
Билет 7. Дать определение эллипса. Записать уравнение эллипса в канонической форме. Вершины, фокусы, оси и эксцентриситет эллипса. Определение: Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами эллипса, есть величина постоянная. Пусть F 1 и F 2 – фокусы эллипса. Начало O системы координат расположим на середине отрезка F 1 F 2. Ось Ox направим вдоль этого отрезка, ось Oy – перпендикулярно к этому отрезку (рис.).
Определение: Точки пересечения эллипса с его осями симметрии называются вершинами эллипс а, центр симметрии – центром эллипса, отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса, половина его длины – большой полуосью эллипса. Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса, половина его длины – малой полуосью. Величина Если эллипс задан каноническими уравнениями, то его вершины имеют координаты (– a;0), (a;0),(0; – b), (0; b), большая полуось равна a, малая полуось равна b. Величина c, являющаяся половиной расстояния между фокусами, определяется из формулы c 2 = a 2 – b 2. Эксцентриситет
Уравнение называется каноническим уравнением эллипса.
Билет 8 Дать определение гиперболы. Записать уравнение гиперболы в канонической форме. Вершины, фокусы, оси, асимптоты и эксцентриситет гиперболы, Определение: Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная. Так же, как и в случае эллипса, для получения уравнения гиперболы выберем подходящую систему координат. Начало координат расположим на середине отрезка между фокусами, ось Ox направим вдоль этого отрезка, а ось ординат – перпендикулярно к нему.
Гипербола обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых лежат фокусы гиперболы, и центром симметрии. Если гипербола задана каноническим уравнением, то ее осями симметрии служат координатные оси Ox и Oy, а начало координат – центр симметрии гиперболы. Определение: Точки пересечения гиперболы, заданной каноническим уравнением с осью Ox называются вершинами гиперболы, отрезок между ними называется действительной осью гиперболы. Отрезок оси ординат между точками (0;– b) и (0; b) называется мнимой осью. Числа a и b называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром. Величина Замечание: Из равенства b 2 = c 2 – a 2 следует, что c > a, то есть у гиперболы
Билет 9. Дать определение параболы. Записать уравнение параболы в канонической форме. Директриса, фокус параболы Параболой называется геометрическое место точек плоскости, равноудаленных от заданной точки F и заданной прямой d, не проходящей через заданную точку. Это геометрическое определение выражает директориальное свойство параболы. Директориальное свойство параболы Точка F называется фокусом параболы, прямая d — директрисой параболы, середина O перпендикуляра, опущенного из фокуса на директрису, — вершиной параболы, расстояние p от фокуса до директрисы — параметром параболы, а расстояние p2 от вершины параболы до её фокуса — фокусным расстоянием (рис,а). Прямая, перпендикулярная директрисе и проходящая через фокус, называется осью параболы (фокальной осью параболы). Отрезок FM, соединяющий произвольную точку M параболы с её фокусом, называется фокальным радиусом точки M. Отрезок, соединяющий две точки параболы, называется хордой параболы. Для произвольной точки параболы отношение расстояния до фокуса к расстоянию до директрисы равно единице. Сравнивая директориальные свойства эллипса, гиперболы и параболы, заключаем, что эксцентриситет параболы по определению равен единице (e=1)(e=1) . Геометрическое определение параболы, выражающее её директориальное свойство, эквивалентно её аналитическому определению — линии, задаваемой каноническим уравнением параболы:
y2=2⋅p⋅x,
Билет 10. Что такое квадратная, единичная, симметрическая, ортогональная матрица. Дать определение транспонированной и обратной матрицы. Определение 1. Матрицей Определение 2. Числа Определение 3. Числа 1.Определение 4. Матрица называется Квадратной если число строк равно числу столбцов. В случае квадратной матрицы вводятся понятия Главной диагонали (это числа — 2.Симметричной (Симметрической) называют квадратную матрицу, элементы которой симметричны относительно главной диагонали. Более формально, симметричной называют такую матрицу Это означает, что она равна её транспонированной матрице:
3. Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны единице. Например, единичной матрицей третьего порядка является матрица
Ортогональная матрица Квадратная матрица A, для которой A-1 = AT называется ортогональной матрицей. Основные свойства ортогональной матрицы: Модуль определителя ортогональной матрицы равен единице. Это свойство следует из свойств определителей: Сумма квадратов элементов любого столбца ортогональной матрицы равна единице. Скалярное произведение строки на саму себя равно 1, а на любую другую строку — 0. Так же и для столбцов. Сумма произведений элементов любой строки ортогональной матрицы на соответствующие элементы другой строки равна нулю. Обратной матрицей называется матрица, которая при умножении как справа, так и слева на данную матрицу дает единичную матрицу.Обозначим обратную матрицу к матрице А через Обратная матрица существует не для всех матриц. Необходимым и достаточным условием невырожденности является det(A) ≠ 0 или rank(A) = N.
Свойства обратной матриц · · · · · · Если необходимо решить систему линейных уравнений Транспонированная матрица — матрица Формально, транспонированная матрица для матрицы
Билет 11. Что такое эквивалентные матрицы. Перечислите элементарные преобразования матриц. Что можно сказать о рангах эквивалентных матриц. Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными. Элементарными преобразованиями над строками матриц называются следующие преобразования строк: 1. умножение строки на ненулевое число; 2. перестановка двух строк; 3. прибавление к одной строке матрицы другой ее строки, умноженной на некоторое ненулевое число. 4. Если от матрицы 5. Метод элементарных преобразований 6. Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.
Билет 12, Что такое базисный минор. Сформулируйте теорему о базисном миноре. Определение. Ранг матрицы А - максимальный порядок неравного нулю минора (минор - определитель квадратной матрицы Определение. Минор, определяющий ранг матрицы, называется Базисным минором. Строки и столбцы, формирующие БМ, называются базисными строками и столбцами. Определение. Система столбцов
Теорема о Базисном миноре Столбцы матрицы В матрице Следствие. Если все столбцы матрицы
Билет 13 Что такое однородная и неоднородная система уравнений. Что называется решением системы уравнений. Поясните термины: совместная система уравнений, несовместная система уравнений. Какие системы уравнений называются эквивалентными? Определение 1. Если все свободные члены равны нулю, то система называется однородной, и неоднородной - в противном случае. Определение 2. Решением системы называется совокупность из n чисел с 1, с 2, …, с n, при подстановке которой в систему вместо неизвестных будет получено m числовых тождеств. Определение 3. Система Определение 4. Совместная система Определение. Две системы линейных уравнений называют равносильными (эквивалентными), если они имеют одни и те же решения. Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются только над строками системы.
Билет 14 Что такое фундаментальная система решений однородной системы уравнений. Что называется общим решением однородной системы уравнений.
Определение. Базис пространства решений системы линейных однородных уравнений называется её фундаментальной системой решений. Теорема о структуре общего решения однородной системы уравнений: Любое решение однородной системы линейных уравнений определяется формулой
где X 1, X 2, …, Xn − r — фундаментальная система решений однородной системы линейных уравнений и C 1, C 2, …, Cn − r — произвольные постоянные. Свойства общего решения однородной системы уравнений: 1. При любых значениях C 1, C 2, …, Cn − r X, определяемое формулой (3), является решением системы (1). 2. Каково бы ни было решение X 0, существуют числа C 10, …, Cn − r 0 такие, что 3.
БиБ Билет 16. Дать определение линейного пространства и сформулировать его свойства. Множество L называется линейным или векторным пространством, если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо: 1. Каждой паре элементов x и y из L отвечает элемент x + y из L, называемый суммой x и y, причём: x + y = y + x − сложение коммутативно; x + (y + z) = (x + y) + z − сложение ассоциативно; x + 0 = x − существует единственный нулевой элемент 0 (x + 0 = x для любого x из L); x + (− x) = 0 − для каждого элемента x из L существует единственный противоположный элемент −x (x + (−x) = 0 для любого x из L). 2. Каждой паре x и α, где α − число, а x элемент из L, отвечает элемент α· x, наываемый произведением α и x, причём: α·(β · x) = (α·β) · x − умножнение на число ассоциативно:; 1 · x = x − для любого элемента x из L. 3. Операции сложения и умножения на число связаны соотношениями: α·(x + y) = α· x + α· y − умножнение на число дистрибутивно относительно сложения элементов; (α + β )· x = α· x + β · x − умножнение на вектор дистрибутивно относительно сложения чисел. Билет 17. Подпространство линейного пространства. Его свойства. Линейная оболочка.
Непустое подмножество L линейного пространства V называется линейным подпространством пространства V, если 1) u+v∈L ∀u,v∈L (подпространство замкнуто по отношению к операции сложения); 2) λv∈L ∀v∈L и любого числа λ (подпространство замкнуто по отношению к операции умножения вектора на число). Свойство 1 Всякое подпространство линейного пространства R есть линейное пространство. Свойство 2 dim M ≤ dim Rn. Свойство 3 (о пополнении базиса). Если (ep)k — базис в подпространстве M линейного пространства Rn, причем k < n, то можно так выбрать элементы в Rn ek+1, ek+2,..., en, что (ep)n будет базисом в Rn. О п р е д е л е н и е.Линейная оболочка — это набор векторов, которые задают линейное подпространство. Строго говоря, линейная оболочка — это множество всех линейных комбинаций данных векторов. Так же обозначим особенности:
Билет 18. Дать определение евклидова пространства. Поясните операцию нормирование вектора. Определение Пусть V — векторное пространство. Говорят, что в V задано скалярное произведение, если любым двум векторам x, y ∈ V поставлено в соответствие действительное число, называемое скалярным произведением этих векторов и обозначаемое через xy или (x, y), так, что выполнены следующие условия (здесь x, y, z — произвольные векторы из V, а t — произвольное действительное число): 1) xy = yx (скалярное произведение коммутативно); 2) (tx)y = t(xy); 3) (x + y)z = xz + yz (скалярное произведение дистрибутивно относительно сложения); 4) xx >=0, причем xx = 0 тогда и только тогда, когда x = 0. Векторное пространство, в котором задано скалярное произведение, называется евклидовым. Свойства 1)–4) называются аксиомами евклидова пространства. Вектор называют нормированным или единичным, если его длина равна единице. Нормировать произвольный ненулевой вектор — это поделить его на длину. Получится единичный вектор, сонаправленный исходному. Билет 19 Что такое ортонормированный базис. Поясните процесс ортогонализации Грама-Шмидта на примере двумерного базиса. Ортонормированная система, состоящая из n векторов n -мерного евклидова пространства, образует базис этого пространства. Такой базис называется ортонормированным базисом. Если e 1, e 2, ..., e n — ортонормированный базис n -мерного евклидова пространства и x = x 1 e1 + x 2 e2 +... + x n e n — разложение вектора x по этому базису, то координаты x i вектора x в ортонормированном базисе вычисляются по формулам x i =(x, e i ), i = 1, 2,..., n. ГРАМА-ШМИДТА, Дана линейно независимая система векторов b1, b2, …, bl, al+1, …, an l ≥ 1 (1)часть, которой ортогональна, обозначим bl+1 ортогональную составляющую вектора аl+1 относительно ортогональной системы b1, b2, …, b l. Тогда1. Система векторов b1, b2, …, bl, bl+1, al+2, …, an (2) эквивалентна (1). 2. Система векторов (2) линейно независима, а ее часть b1, b2, …, bl, bl+1 – ортогональна.Используя, понятие ортогональной составляющей, опишем процесс превращения линейно независимой системы а1, а2, …, аn в ортогональную систему b1, b2, …, bn ненулевых векторов, который называется ортогонализацией системы а1, а2, …, аn. Этот процесс состоит из n–шагов, n–число векторов в исходной системе а1, а2, …, аn. 1 шаг. Полагаем b1=а1 и получаем систему b1, а2, …, аn 2 шаг. Заменим в системе (3) вектор а2 ортогональной составляющей относительно b1, и получим систему: b1,b2, а3,…,аn (4) Согласно шагам ортогонализации система (4) линейно независима, а ее часть b1, b2 –ортогональна. Предположим, что уже построена линейно независимая система b1, b2, …, bk-1, ak,…, an, (5) у которой b1, b2, …, bk-1 – ортогональны. На k-том шаге k = 3, n заменим в системе (5) вектор ak его ортогональной составляющей относительно системы b1, b2, …, bk-1 и получим систему b1, …,bk, ak+1, …, an. После выполнения n–го шага получим линейно независимую и ортогональную систему векторов b1, b2, …, bn. Билет 20. Дать определение оператора в линейном пространстве. Какой оператор называется линейным. Оператором называется правило, по которому каждому элементу x некоторого непустого множества X ставится в соответствие единственный элемент y некоторого непустого множества Y. Говорят, что оператор действует из X в Y. Действие оператора обозначают y = A (x), y — образ x, x — прообраз y. Если каждый элемнт y из Y имеет единственный прообраз x из X, y = A (x), оператор называют взаимно однозначным отображением X в Y или преобразованием X, X — область определения оператора. Пусть X и Y два линейные пространства. Оператор A, действующий из X в Y, называется линейным оператором, если для любых двух элементов u и v из X и любого числа α справедливо: A (u + v) = A (u) + A (v), A (α· u) = α· A (u).
Билет 21. Приведите пример линейного оператора. Какие действия над линейными операторами Вы знаете?
|
||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 753; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |



 Рассмотрим векторы
Рассмотрим векторы  и
и  . Если угол между ними острый, то он будет
. Если угол между ними острый, то он будет  , где φ – угол между прямой и плоскостью. Тогда
, где φ – угол между прямой и плоскостью. Тогда  .
. и
и  . Следовательно
. Следовательно  . Поэтому в любом случае
. Поэтому в любом случае  . Вспомнив формулу вычисления косинуса угла между векторами, получим
. Вспомнив формулу вычисления косинуса угла между векторами, получим  .
. .
.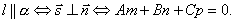
 называется эксцентриситетом эллипса.
называется эксцентриситетом эллипса. эллипса характеризует степень вытянутости эллипса. Чем ближе эксцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса 0<
эллипса характеризует степень вытянутости эллипса. Чем ближе эксцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса 0<  .
.
 . Уравнение называется каноническим уравнением гиперболы.
. Уравнение называется каноническим уравнением гиперболы.

 называется прямоугольная таблица из чисел, содержащая
называется прямоугольная таблица из чисел, содержащая  — строк и
— строк и  — столбцов..
— столбцов.. , входящие в состав данной матрицы, называются ее элементами.
, входящие в состав данной матрицы, называются ее элементами. ) и Побочной диагонали (это числа —
) и Побочной диагонали (это числа —  ).
). , что
, что 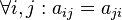 .
. .
.


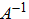 , тогда согласно определению получим:
, тогда согласно определению получим: 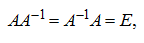 где Е – единичная матрица.
где Е – единичная матрица.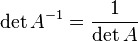 , где
, где 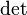 обозначает определитель.
обозначает определитель.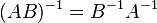 для любых двух обратимых матриц
для любых двух обратимых матриц 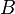 .
.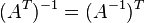 , где
, где 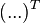 обозначает транспонированную матрицу.
обозначает транспонированную матрицу.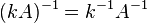 для любого коэффициента
для любого коэффициента 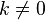 .
.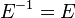 .
. , (b — ненулевой вектор) где
, (b — ненулевой вектор) где 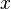 — искомый вектор, и если
— искомый вектор, и если 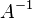 существует, то
существует, то 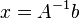 . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.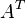 , полученная из исходной матрицы
, полученная из исходной матрицы 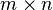 — матрица
— матрица 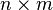 , определённая как
, определённая как 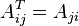 .
. к матрице
к матрице 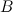 перешли с помощью эквивалентных преобразований над строками, то такие матрицы называются эквивалентными и обозначают
перешли с помощью эквивалентных преобразований над строками, то такие матрицы называются эквивалентными и обозначают 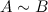 .
.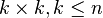 ). Обозначается
). Обозначается  .
.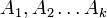 называется линейно зависимой
называется линейно зависимой 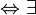 числа
числа 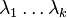 , не все равные нулю и такие что:
, не все равные нулю и такие что: 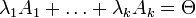
 минор
минор  -го порядка называется базисным, если он отличен от нуля, а все миноры
-го порядка называется базисным, если он отличен от нуля, а все миноры 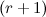 -ro порядка равны нулю или их вообще не существует.
-ro порядка равны нулю или их вообще не существует.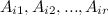 , которые образуютлинейно независимую систему, то ранг матрицы
, которые образуютлинейно независимую систему, то ранг матрицы  .
. называется совместной (несовместной), если она имеет хотя бы одно решение (не имеет решений).
называется совместной (несовместной), если она имеет хотя бы одно решение (не имеет решений).