
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение интегральных уравнений Вольтерра методом дифференцированияСодержание книги
Поиск на нашем сайте
Некоторые интегральные уравнения Вольтерра, как первого, так и второго рода решаются методом дифференцирования. Рассмотрим уравнение Вольтерра второго рода
Продифференцируем данное уравнение
применив правило дифференцирования интеграла по параметру x ( В случае вырожденных ядер можно применить правило дифференцирования произведения, предварительно вынося множитель зависящий только от Исключая неизвестный интеграл из двух уравнений, данного и полученного после дифференцирования, получим дифференциальное уравнение первого порядка. Если после первого дифференцирования исключить интеграл от неизвестной функции не удаётся можно попытаться осуществить исключение после n-кратного дифференцирования. Особенно метод эффективен, если после n-кратного дифференцирования удаётся производную
Пример 2. Найти решение уравнения Вольтерра второго рода
Решение. Дифференцируем данное уравнение
и решаем полученное дифференциальное уравнение
при начальном условии
Ответ:
Проверка. Найденную функцию подставляем в исходное уравнение
и вычислив интегралы, получим тождество
Следовательно, эта функция удовлетворяет заданному равнению и является его решением.
Пример 3. Найти решение уравнения Вольтерра первого рода.
Решение. Дифференцируем данное уравнение
и заменив неизвестный интеграл его значением из данного уравнения
найдём решение дифференциального уравнения.
Ответ:
Проверка. Подставим полученную функцию в исходное уравнение
откуда получаем тождество
Решение интегральных уравнений с помощью Степенных рядов Для уравнений Вольтерра второго рода
будем искать решение в виде степенного ряда
Подставим ряд (5.2) в уравнение (5.1)
и положив Затем, дифференцируя равенство (5.3) по
Откуда, при Аналогично найдем В общем случае записать рекуррентную формулу для нахождения
Для некоторых частных видов уравнений найти решение интегрального уравнения Вольтерра бывает не сложно. Приведем пример.
Пример 4. Найти решение уравнения
Решение. Будем искать решение в виде степенного ряда Подставим этот ряд в данное уравнение
и, положив
и снова положив
И положив
откуда при
Продифференцировав ещё раз найдём откуда при
Нетрудно проверить, что получен точный ответ.
Решение интегральных уравнений Вольтерра методом последовательных приближений Уравнение второго рода
Теорема 1. Уравнение (6.1), если свободная функция
Доказательство. Примем за начальное приближение свободную функцию Выпишем рекуррентную формулу последовательных приближений по методу Пикара
В соответствии с условием теоремы имеем ограничения
…..………………………………………………………………………
…………………………………………………………………………..
при 0!=1.
Положим далее x = b, b > a и b любое, тогда
Как видим оценка Действительно
Ряд в неравенстве (6.3) по построению является мажорирующим для ряда
частичная сумма которого равна Тогда по критерию Вейерштрасса ряд (6.4) сходится абсолютно и равномерно и, следовательно, имеет непрерывную сумму
Остается доказать, что эта непрерывная функция
и в силу теоремы о единственности предела имеем
Методом от противного докажем единственность полученного решения. Предположим, что существует другое решение
Вычтем из тождества (6.5) тождество (6.6) и оценим по модулю эту разность
Неравенство (6.7) должно выполняться для всех значений
Пример 5. Применив метод последовательных приближений найти приближённое решение уравнения
на отрезке
Решение. За начальное приближение примем свободную
функцию
Затем находим
следовательно
За приближённое решение примем
тогда по теореме Лейбница для знакочередующихся рядов погрешность не превосходит максимума первого члена отброшенного остатка ряда, т.е.
Чтобы удовлетворить требуемую точность необходимо положить
тогда по той же теореме Лейбница имеем гарантированную погрешность
И так условие задачи выполнено.
Уравнения первого рода
Теорема 2. Если в уравнении (6.8) ядро
Доказательство. Продифференцируем уравнение (6.8)
Если
Если
Пример 6. Найти решение интегрального уравнения первого рода
Решение. Дифференцируя данное уравнение найдём
и к полученному интегральному уравнению Вольтерра второго рода
применим метод последовательных приближений. Выпишем рекуррентную формулу
и приняв за начальное приближение
Далее находим
Выпишем последовательность полученных приближений к искомому решению
или для данной задачи имеем
Нетрудно заметить, что пределом найденной числовой последовательности является число равное 1, следовательно искомая функция постоянна и равна единице. Ответ: Сделаем проверку подставив решение в исходное уравнение
Найденное решение удовлетворяет уравнению.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 7221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.43 (0.009 с.) |


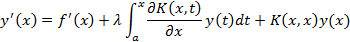
 - переменная вне интеграла).
- переменная вне интеграла). выразить через ядро
выразить через ядро  . Это легко удаётся осуществить, например, для следующих функций
. Это легко удаётся осуществить, например, для следующих функций  и др.
и др.



 находим значение постоянной
находим значение постоянной 
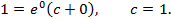



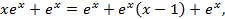
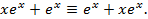
 .
.

 .
.
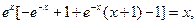

 (5.1)
(5.1)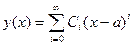 . (5.2)
. (5.2) (5.3)
(5.3) , найдем
, найдем 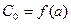 .
. и, полагая после каждого дифференцирования
и, полагая после каждого дифференцирования 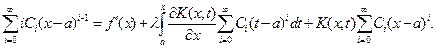 (5.
(5.  )
)
 для
для 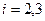 ,... Следующие коэффициенты определяются через значения
,... Следующие коэффициенты определяются через значения  и предыдущие коэффициенты.
и предыдущие коэффициенты. .
.
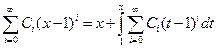 (*)
(*)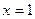 , найдем
, найдем  . Затем дифференцируем равенство (*)
. Затем дифференцируем равенство (*) (**)
(**) , т.е.
, т.е.  . Далее дифференцируем равенство (**)
. Далее дифференцируем равенство (**)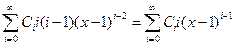

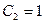 . Продолжаем те же операции далее
. Продолжаем те же операции далее
 получим
получим
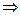
 .
.
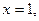 получим
получим ,
,  и т.д.
и т.д. 
 .
. 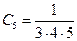 ,
,  …
…
 (6.1)
(6.1) и ядро
и ядро  - непрерывные функции при
- непрерывные функции при  , имеет единственное непрерывное решение при любом значении параметра
, имеет единственное непрерывное решение при любом значении параметра  . Это решение может быть найдено методом последовательных приближений.
. Это решение может быть найдено методом последовательных приближений. .
.
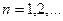 (6.2)
(6.2) и
и  используя которые оценим последовательные приближения (6.2) по модулю
используя которые оценим последовательные приближения (6.2) по модулю ,
,



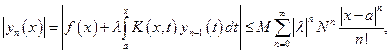
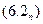

 (6.3)
(6.3) го приближения к решению дается числовым рядом, который по признаку Даламбера сходится.
го приближения к решению дается числовым рядом, который по признаку Даламбера сходится.
 (6.4)
(6.4)

 является решением уравнения (6.1). Для этого в равенстве (6.2) перейдем к пределу
является решением уравнения (6.1). Для этого в равенстве (6.2) перейдем к пределу
 . (6.5)
. (6.5)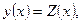 тогда выполняется тождество
тогда выполняется тождество . (6.6)
. (6.6) (6.7)
(6.7) следовательно оно выполняется и для
следовательно оно выполняется и для  и пусть этот максимум достигается в точке
и пусть этот максимум достигается в точке  , тогда имеем неравенство
, тогда имеем неравенство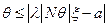 или
или  откуда
откуда 
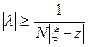 , что противоречит ранее доказанному, что
, что противоречит ранее доказанному, что 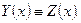 Единственность доказана.
Единственность доказана.
 с точностью
с точностью 
 тогда
тогда .
.
 Далее по индукции выписываем
Далее по индукции выписываем ,
, .
.
 ,
, .
. ,
,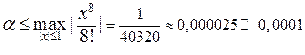 .
. . (6.8)
. (6.8) то уравнение (6.8) имеет единственное непрерывное решение при дополнительных условиях
то уравнение (6.8) имеет единственное непрерывное решение при дополнительных условиях 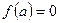 и
и  что
что  Это решение может быть найдено методом последовательных приближением сведением к интегральному уравнению Вольтерра второго рода после
Это решение может быть найдено методом последовательных приближением сведением к интегральному уравнению Вольтерра второго рода после  -кратного дифференцирования.
-кратного дифференцирования. . (6.9)
. (6.9) , то деля равенство (6.9) на этот множитель получим интегральное уравнение Вольтерра второго рода
, то деля равенство (6.9) на этот множитель получим интегральное уравнение Вольтерра второго рода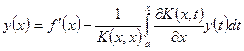 , (6.10) решение которого существует и при том единственное по теореме 1.
, (6.10) решение которого существует и при том единственное по теореме 1. , то дифференцируя равенство (6.10) и поделив полученное равенство на
, то дифференцируя равенство (6.10) и поделив полученное равенство на  , при условии
, при условии  , получим интегральное уравнение Вольтерра второго рода. Аналогично поступаем и в случае если
, получим интегральное уравнение Вольтерра второго рода. Аналогично поступаем и в случае если 



 , вычислим
, вычислим .
. ,
,  ,
, ,
,  ,
,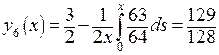 и так далее.
и так далее.
 .
. .
. ,
, 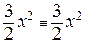 .
.


