
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация интегральных уравненийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Г.А.Шишкин Линейные интегральные Уравнения Вольтерра
Улан-Удэ
МИНИСТЕРСТВО ОБРАЗОВАНИя И Науки российской федерации Бурятский государственный университет
Г.А.Шишкин Линейные интегральные Уравнения Вольтерра Учебное пособие по спецкурсу и спецсеминару Рекомендовано Учебно-методическим советом БГУ в качестве учебного пособия для студентов направления 010400.62 «Прикладная математика и информатика»
Улан-Удэ Издательство Бурятского Госуниверситета
УДК 511 968 Ш 655
Утверждено к печати редакционно-издательским советом Бурятского госуниверситета Р е ц е н з е н т ы А.Д. Мижидон, д-р техн. наук, проф. В.В. Кибирев, канд. физ-мат. наук, проф.
Шишкин Г.А. Ш 655 Линейные интегральные уравнения Вольтерра: учебное пособие. – Улан-Удэ: Издательство Бурятского госуниверситета, 2012. - 59 с.
В учебном пособии кратко изложены основные разделы теории интегральных уравнений Вольтерра. Главное внимание уделено изложению вопросов, касающихся типов уравнений и методов их решения. Рассмотрена теорема существования и единственности решения и ряд других наиболее важных теорем. К каждому типу уравнений и рассмотренных в пособии методов их решения приведены примеры с решениями, в последнем параграфе дан список задач для самостоятельного решения. Пособие предназначено студентам специальности «Прикладная математика и информатика», может использоваться студентами специальностей: «Математика», «Математическое обеспечение и администрирование информационных систем», «Математические методы в экономике» «Физика» и др.
© Шишкин Г.А., 2012 © Бурятский госуниверситет, 2012
Введение Уравнение называют интегральным, если неизвестная функция входит в уравнение под знаком интеграла. Интегральные уравнения – это функциональные уравнения специального типа, история которых тесно связана с задачами математической физики, в частности с проблемой колебания твердого тела [16]. Теория интегральных уравнений составляет значительный раздел математического анализа и имеет большое теоретическое и прикладное значение. В настоящее время всё чаще интегральные уравнения рассматривают как самостоятельную дисциплину. Отдельные интегральные уравнения встречались уже в первой половине XIX в., но систематическая их теория была заложена на рубеже XIX и XX вв. в работах итальянского математика В.Вольтерра (1860-1940), шведского математика И. Фредгольма (1866-1927), Д. Гильберта (1862-1943) и других математиков [31]. Этот предмет имеет долгую и извилистую историю. Своим возникновением он обязан Даниилу Бернулли и затем в течение двух столетий усилия математиков были направлены на решение проблемы колебаний среды (механической, акустической, оптической, электромагнитной) и связанной с ней краевой задачей теории потенциала, которая сводится к решению интегральных уравнений. Один из первых, если не первый, результат, который можно связать с интегральными уравнениями, это формулы обращения Фурье(1811):
Можно считать, что формула (2) дает решение интегрального уравнения (1), в котором !!! Работа Фурье «Théorie analy lique delachaleur» (1822) стала вехой на этом пути. Г. А. Шварц с помощью построения основной частоты мембраны впервые доказал (1885) существование собственных колебаний для двумерного случая и более высоких размерностей. Последнее десятилетие XIX века пришлось на создание Пуанкаре его мощных теоретико-функциональных методов. Вместе с К. Нейманом они приступили к рассмотрению гармонической краевой задачи, которая сводилась к решению интегрального уравнения. Однако тот факт, что в более простых ситуациях в непрерывном предельном случае возникают дифференциальные, а не интегральные уравнения, на целых два столетия приковал внимание математиков к дифференциальным уравнениям. Важным моментом в изучении линейных интегральных уравнений явилась работа Вольтерра (1896), в которой он исследовал уравнения вида
где В 1900 Э.И. Фредгольм изложил основные свойства и теоремы теории линейных интегральных уравнений с постоянными пределами интегрирования, разработал общие методы решения этого вида уравнений, которые теперь называют уравнениями типа Фредгольма. Фредгольм дал красивое и оригинальное решение этого класса уравнений, которое открывало некоторую аналогию между интегральными уравнениями и алгебраическими линейными уравнениями. В работах Фредгольма была реализована также идея превращения системы линейных уравнений, описывающей дискретную систему масс, в интегральные уравнения при переходе к предельному случаю сплошной среды. Тем не менее, надо отметить, что результаты Фредгольма вытекают из специального вида его уравнения, которое возникает при решении проблем математической физики [16]. Уравнения Вольтерра второго рода типичны при описании физических процессов, связанных с явлениями последействия. В этих уравнениях переменная x обычно обозначает время. Тогда состояние системы, характеризуемое функцией Интегральные уравнения встречаются в различных областях науки и многочисленных приложениях (в теории упругости, теории пластичности, гидродинамике, теории массопереноса и теплопереноса, теории управления, химической технологии, биомеханике, теории массового обслуживания, экономике, медицине и др.). Интегральные уравнения Вольтерра имеют широкую область применения в прикладных задачах и для них были разработаны эффективные методы решения [7],[20] и др. Целью настоящего пособия является рассмотрение основных методов аналитического решения линейных интегральных уравнений Вольтерра.
Задача o таутохроне Найти кривую, скользя вдоль которой без трения тяжелая частица достигает своего самого низкого положения за одно и то же время независимо от её начального положения.
Решение. Выполним чертеж
и введем обозначения Далее воспользовавшись формулой из физики
и формулами из курса математического анализа
подставим формулы (2.2) в равенство (2.1)
Введем обозначение
Полученное равенство (2.3) проинтегрируем по t (0≤ t ≤ T), в то же время
откуда
Интегральное уравнение вида (2.4) есть уравнение Вольтерра первого рода, где u(x) - неизвестная функция. Решение таких уравнений впервые предложил Абель и поэтому уравнения такого вида называются уравнениями Абеля.
Высших порядков
Положим
тогда
где
и по формуле Коши для кратного интегрирования имеем
…………………………………………………………
………………………………………………………
Найдем дифференциальный оператор
Введем обозначения
Тогда выражение для дифференциального оператора
и вводя обозначение g(x) = f(x) –
которое эквивалентно первоначальной задаче.
Степенных рядов Для уравнений Вольтерра второго рода
будем искать решение в виде степенного ряда
Подставим ряд (5.2) в уравнение (5.1)
и положив Затем, дифференцируя равенство (5.3) по
Откуда, при Аналогично найдем В общем случае записать рекуррентную формулу для нахождения
Для некоторых частных видов уравнений найти решение интегрального уравнения Вольтерра бывает не сложно. Приведем пример.
Пример 4. Найти решение уравнения
Решение. Будем искать решение в виде степенного ряда Подставим этот ряд в данное уравнение
и, положив
и снова положив
И положив
откуда при
Продифференцировав ещё раз найдём откуда при
Нетрудно проверить, что получен точный ответ.
Уравнение второго рода
Теорема 1. Уравнение (6.1), если свободная функция
Доказательство. Примем за начальное приближение свободную функцию Выпишем рекуррентную формулу последовательных приближений по методу Пикара
В соответствии с условием теоремы имеем ограничения
…..………………………………………………………………………
…………………………………………………………………………..
при 0!=1.
Положим далее x = b, b > a и b любое, тогда
Как видим оценка Действительно
Ряд в неравенстве (6.3) по построению является мажорирующим для ряда
частичная сумма которого равна Тогда по критерию Вейерштрасса ряд (6.4) сходится абсолютно и равномерно и, следовательно, имеет непрерывную сумму
Остается доказать, что эта непрерывная функция
и в силу теоремы о единственности предела имеем
Методом от противного докажем единственность полученного решения. Предположим, что существует другое решение
Вычтем из тождества (6.5) тождество (6.6) и оценим по модулю эту разность
Неравенство (6.7) должно выполняться для всех значений
Пример 5. Применив метод последовательных приближений найти приближённое решение уравнения
на отрезке
Решение. За начальное приближение примем свободную
функцию
Затем находим
следовательно
За приближённое решение примем
тогда по теореме Лейбница для знакочередующихся рядов погрешность не превосходит максимума первого члена отброшенного остатка ряда, т.е.
Чтобы удовлетворить требуемую точность необходимо положить
тогда по той же теореме Лейбница имеем гарантированную погрешность
И так условие задачи выполнено.
Уравнения первого рода
Теорема 2. Если в уравнении (6.8) ядро
Доказательство. Продифференцируем уравнение (6.8)
Если
Если
Пример 6. Найти решение интегрального уравнения первого рода
Решение. Дифференцируя данное уравнение найдём
и к полученному интегральному уравнению Вольтерра второго рода
применим метод последовательных приближений. Выпишем рекуррентную формулу
и приняв за начальное приближение
Далее находим
Выпишем последовательность полученных приближений к искомому решению
или для данной задачи имеем
Нетрудно заметить, что пределом найденной числовой последовательности является число равное 1, следовательно искомая функция постоянна и равна единице. Ответ: Сделаем проверку подставив решение в исходное уравнение
Найденное решение удовлетворяет уравнению.
Литература
1. Васильева А.Б., Медведев Т.Н., Тихонов Н.А., Уразгильдина Т.А. «Дифференциальные и интегральные уравнения. Вариационное исчисление» - М., 2003. 2. Васильева А. Б., Тихонов Н. А. «Интегральные уравнения» - М.: Физматлит, 2002. 3. Виарда Г. Интегральные уравнения, ГТТИ, 1933. 4. Вольтерра В., Теория функционалов, интегральных и интегро-дифференциальных уравнений. – М.: Наука, 1982. 5. Вольтерра В. Математическая теория борьбы за существование. Наука, физматлит. М, 1976. -286с. 6. Трикоми Ф. Интегральные уравнения. ИЛ, 1960. 7. Забрейко П. П., Кошелев А. И. и др. Интегральные уравнения. – М.: Наука, 1968. 8. Канторович Л. В., Крылов В. И. Приближенные методы высшего анализа. – М.: Наука, 1962. 9. Краснов М. Л. Интегральные уравнения. Введение в теорию. – М.: Наука, 1975. 10. Краснов М. Л., Кисилев А. И., Макаренко Г. И. «Интегральные уравнения» - М.: УРСС., 2003. 11. Лизоркин П. И. Курс дифференциальных и интегральных уравнений с дополнительными главами анализа. – М.: Наука, 1965. 12. Ловит У. В. Линейные интегральные уравнения. – М.: Госиздат., 1957. – 266с. 13. Люстерник Л. А., Соболев В. И. Краткий курс функционального анализа. // М.: Высшая школа, 1982. 14. Миргород В.Ф. «Обобщение методов аналитического решения некоторых типов интегральных уравнений Вольтерра второго рода»/ ОАО «Элемент», г. Одесса, Украина 2009. 15. Михлин С. Г. «Интегральные уравнения и их приложения» - М.: ОГИЗ., 1949. 16. Михлин С. Г. Лекции по линейным интегральным уравнениям. Физматгиз, 1959. 17. Михлин С. Г., Смолицкий Х. Л. Приближенные методы решения дифференциальных и интегральных уравнений. – М.: Наука, 1965. 18. Петровский И. Г. «Лекции по теории интегральных уравнений» - М.: УРСС., 2003. 19. Привалов И. И. Интегральные уравнения. ОНТИ, 1937. 20. Полянин А. Д., Манжирова А. В. «Справочник по интегральным уравнениям» - М.: Физматлит, 2003. 21. Тихонов А. Н., Самарский А. А. «Численные методы» 22. Цлаф Л. Я. «Вариационное исчисление и интегральные уравнения» - издательство «Лань», 2005. 23. Volterra V. Lesons sur les equations integrals et les equations integrals et les equations integrodifferentielles. - Paris.1913 24. Volterra V. Varigzioni e fluttuzioni del numero d' indivindin specie animali conviventi // R. Comit Tallas. Jt. Met.31.1927. 25. Volterra V. La teoria deifunzionall appiata aifenomene ereditari // Atti congr.lut. Mat., Bolongna,v.1,1928. 26. Volterra V. Sulla inversion degli integrali definite. Rend. Accad. Lincei, 1896, 5. p. 177-185. 27. Volterra V. Theory of functional and of integral and integro – differenstial equations. - London – Grasqov, 1930. 28. Volterra V. Theory of functional and of integral and integro – differenstial equations.- London 1931. 29. Volterra V. The general equations of biological strife in the case of historical actions // Proc. Edinburgh Math.Soc.6.1939.- C/ 4-10. 30. www.intuit.ru 31. www.wikipedia.ru 32. www.eqworld.ipmnet.ru 33. www.yabotanik.ru
СОДЕРЖАНИЕ Введение…………………………………………………………………. 3 §1. Классификация интегральных уравнений Вольтерра……………...7 §2. Задачи, приводящие к интегральным уравнениям Вольтерра…...11 §3. Интегральные уравнения Вольтерра как частный случай уравнений Фредгольма…………………………………………………19 §4. Решение интегральных уравнений Вольтерра методом дифференцирования…………………………………………………….20 §5. Решение интегральных уравнений Вольтерра с помощью степенных рядов………………………………………………………...22 §6. Решение интегральных уравнений Вольтерра методом последовательных приближений………………………………………25 §7. Уравнения с вырожденными ядрами………………………………32 §8. Решение уравнений Вольтерра с помощью ряда Неймана………37 §9. Итерированные ядра и резольвента интегральных уравнений Вольтерра………………………………………………………………..40 §10.Ррешение уравнений Вольтерра с разностными ядрами с помощью преобразования Лапласа…………………………………….45 §11. Задания для самостоятельного решения…………………………55 Литература………………………………………………………………60
Г.А.Шишкин Линейные интегральные Уравнения Вольтерра
Улан-Удэ
МИНИСТЕРСТВО ОБРАЗОВАНИя И Науки российской федерации Бурятский государственный университет
Г.А.Шишкин Линейные интегральные Уравнения Вольтерра Учебное пособие по спецкурсу и спецсеминару Рекомендовано Учебно-методическим советом БГУ в качестве учебного пособия для студентов направления 010400.62 «Прикладная математика и информатика»
Улан-Удэ Издательство Бурятского Госуниверситета
УДК 511 968 Ш 655
Утверждено к печати редакционно-издательским советом Бурятского госуниверситета Р е ц е н з е н т ы А.Д. Мижидон, д-р техн. наук, проф. В.В. Кибирев, канд. физ-мат. наук, проф.
Шишкин Г.А. Ш 655 Линейные интегральные уравнения Вольтерра: учебное пособие. – Улан-Удэ: Издательство Бурятского госуниверситета, 2012. - 59 с.
В учебном пособии кратко изложены основные разделы теории интегральных уравнений Вольтерра. Главное внимание уделено изложению вопросов, касающихся типов уравнений и методов их решения. Рассмотрена теорема существования и единственности решения и ряд других наиболее важных теорем. К каждому типу уравнений и рассмотренных в пособии методов их решения приведены примеры с решениями, в последнем параграфе дан список задач для самостоятельного решения. Пособие предназначено студентам специальности «Прикладная математика и информатика», может использоваться студентами специальностей: «Математика», «Математическое обеспечение и администрирование информационных систем», «Математические методы в экономике» «Физика» и др.
© Шишкин Г.А., 2012 © Бурятский госуниверситет, 2012
Введение Уравнение называют интегральным, если неизвестная функция входит в уравнение под знаком интеграла. Интегральные уравнения – это функциональные уравнения специального типа, история которых тесно связана с задачами математической физики, в частности с проблемой колебания твердого тела [16]. Теория интегральных уравнений составляет значительный раздел математического анализа и имеет большое теоретическое и прикладное значение. В настоящее время всё чаще интегральные уравнения рассматривают как самостоятельную дисциплину. Отдельные интегральные уравнения встречались уже в первой половине XIX в., но систематическая их теория была заложена на рубеже XIX и XX вв. в работах итальянского математика В.Вольтерра (1860-1940), шведского математика И. Фредгольма (1866-1927), Д. Гильберта (1862-1943) и других математиков [31]. Этот предмет имеет долгую и извилистую историю. Своим возникновением он обязан Даниилу Бернулли и затем в течение двух столетий усилия математиков были направлены на решение проблемы колебаний среды (механической, акустической, оптической, электромагнитной) и связанной с ней краевой задачей теории потенциала, которая сводится к решению интегральных уравнений. Один из первых, если не первый, результат, который можно связать с интегральными уравнениями, это формулы обращения Фурье(1811):
Можно считать, что формула (2) дает решение интегрального уравнения (1), в котором !!! Работа Фурье «Théorie analy lique delachaleur» (1822) стала вехой на этом пути. Г. А. Шварц с помощью построения основной частоты мембраны впервые доказал (1885) существование собственных колебаний для двумерного случая и более высоких размерностей. Последнее десятилетие XIX века пришлось на создание Пуанкаре его мощных теоретико-функциональных методов. Вместе с К. Нейманом они приступили к рассмотрению гармонической краевой задачи, которая сводилась к решению интегрального уравнения. Однако тот факт, что в более простых ситуациях в непрерывном предельном случае возникают дифференциальные, а не интегральные уравнения, на целых два столетия приковал внимание математиков к дифференциальным уравнениям. Важным моментом в изучении линейных интегральных уравнений явилась работа Вольтерра (1896), в которой он исследовал уравнения вида
где В 1900 Э.И. Фредгольм изложил основные свойства и теоремы теории линейных интегральных уравнений с постоянными пределами интегрирования, разработал общие методы решения этого вида уравнений, которые теперь называют уравнениями типа Фредгольма. Фредгольм дал красивое и оригинальное решение этого класса уравнений, которое открывало некоторую аналогию между интегральными уравнениями и алгебраическими линейными уравнениями. В работах Фредгольма была реализована также идея превращения системы линейных уравнений, описывающей дискретную систему масс, в интегральные уравнения при переходе к предельному случаю сплошной среды. Тем не менее, надо отметить, что результаты Фредгольма вытекают из специального вида его уравнения, которое возникает при решении проблем математической физики [16]. Уравнения Вольтерра второго рода типичны при описании физических процессов, связанных с явлениями последействия. В этих уравнениях переменная x обычно обозначает время. Тогда состояние системы, характеризуемое функцией
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 723; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.163.120 (0.014 с.) |



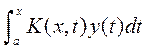
 2012
2012

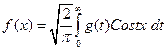 , (1)
, (1)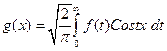 . (2)
. (2)
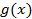 – неизвестная, а
– неизвестная, а 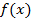 - данная функция.
- данная функция.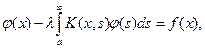 (3)
(3)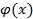 неизвестная функция,
неизвестная функция, 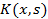 и
и 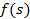 данные функции,
данные функции, 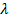 - численный параметр, и доказал, что если
- численный параметр, и доказал, что если 
 , Т – постоянная величина,
, Т – постоянная величина,  - функция от h, кривую будем искать в виде
- функция от h, кривую будем искать в виде 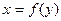 .
. (2.1)
(2.1) , где
, где 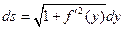 , (2.2)
, (2.2) , откуда
, откуда  .
.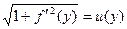 и так как с течением времени функция s(t) убывает, то оставляем знак минус
и так как с течением времени функция s(t) убывает, то оставляем знак минус . (2.3)
. (2.3)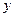 изменяется от h до 0 (h ≥
изменяется от h до 0 (h ≥ 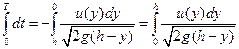 ,
,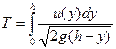 . (2.4)
. (2.4)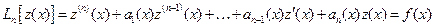 ,
,  ,
, 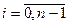 , где
, где  . (2.6)
. (2.6)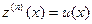 (2.7)
(2.7) ,
, – любое из отрезка [ a, b ] при нахождении общего решения и
– любое из отрезка [ a, b ] при нахождении общего решения и 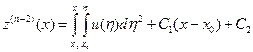
 ,
,
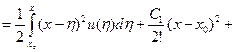

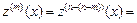
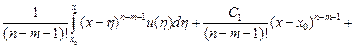
 ,
,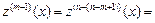
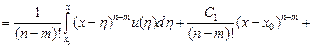
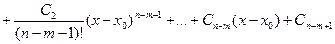 ,
,
 ,
,
 . (2.8)
. (2.8)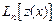 , подставив в него полученные выражения для функции
, подставив в него полученные выражения для функции 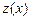 и её производных
и её производных 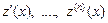



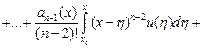





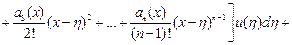



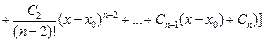 .
.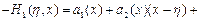
 ,
,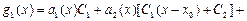


 .
.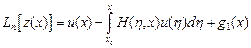
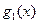 придем к разрешающему интегральному уравнению
придем к разрешающему интегральному уравнению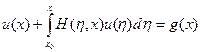 , (2.9)
, (2.9) (5.1)
(5.1)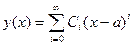 . (5.2)
. (5.2) (5.3)
(5.3) , найдем
, найдем 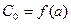 .
. и, полагая после каждого дифференцирования
и, полагая после каждого дифференцирования 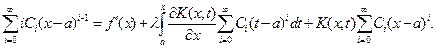 (5.
(5.  )
)
 для
для 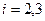 ,... Следующие коэффициенты определяются через значения
,... Следующие коэффициенты определяются через значения  и предыдущие коэффициенты.
и предыдущие коэффициенты. .
.
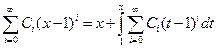 (*)
(*)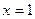 , найдем
, найдем  . Затем дифференцируем равенство (*)
. Затем дифференцируем равенство (*) (**)
(**) , т.е.
, т.е.  . Далее дифференцируем равенство (**)
. Далее дифференцируем равенство (**)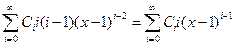

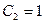 . Продолжаем те же операции далее
. Продолжаем те же операции далее
 получим
получим
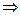
 .
.
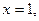 получим
получим ,
,  и т.д.
и т.д. 
 .
. 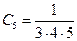 ,
,  …
…
 (6.1)
(6.1) и ядро
и ядро  - непрерывные функции при
- непрерывные функции при  , имеет единственное непрерывное решение при любом значении параметра
, имеет единственное непрерывное решение при любом значении параметра  . Это решение может быть найдено методом последовательных приближений.
. Это решение может быть найдено методом последовательных приближений. .
.
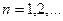 (6.2)
(6.2) и
и  используя которые оценим последовательные приближения (6.2) по модулю
используя которые оценим последовательные приближения (6.2) по модулю ,
,



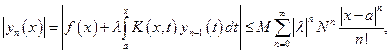
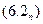
 (6.3)
(6.3) го приближения к решению дается числовым рядом, который по признаку Даламбера сходится.
го приближения к решению дается числовым рядом, который по признаку Даламбера сходится.
 (6.4)
(6.4)

 является решением уравнения (6.1). Для этого в равенстве (6.2) перейдем к пределу
является решением уравнения (6.1). Для этого в равенстве (6.2) перейдем к пределу
 . (6.5)
. (6.5)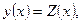 тогда выполняется тождество
тогда выполняется тождество . (6.6)
. (6.6) (6.7)
(6.7) следовательно оно выполняется и для
следовательно оно выполняется и для  и пусть этот максимум достигается в точке
и пусть этот максимум достигается в точке  , тогда имеем неравенство
, тогда имеем неравенство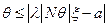 или
или  откуда
откуда 
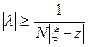 , что противоречит ранее доказанному, что
, что противоречит ранее доказанному, что 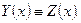 Единственность доказана.
Единственность доказана.
 с точностью
с точностью 
 тогда
тогда .
.
 Далее по индукции выписываем
Далее по индукции выписываем ,
, .
.
 ,
, .
. ,
,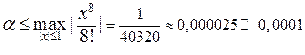 .
. . (6.8)
. (6.8) то уравнение (6.8) имеет единственное непрерывное решение при дополнительных условиях
то уравнение (6.8) имеет единственное непрерывное решение при дополнительных условиях 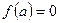 и
и  что
что  Это решение может быть найдено методом последовательных приближением сведением к интегральному уравнению Вольтерра второго рода после
Это решение может быть найдено методом последовательных приближением сведением к интегральному уравнению Вольтерра второго рода после  -кратного дифференцирования.
-кратного дифференцирования. . (6.9)
. (6.9) , то деля равенство (6.9) на этот множитель получим интегральное уравнение Вольтерра второго рода
, то деля равенство (6.9) на этот множитель получим интегральное уравнение Вольтерра второго рода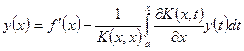 , (6.10) решение которого существует и при том единственное по теореме 1.
, (6.10) решение которого существует и при том единственное по теореме 1. , то дифференцируя равенство (6.10) и поделив полученное равенство на
, то дифференцируя равенство (6.10) и поделив полученное равенство на  , при условии
, при условии  , получим интегральное уравнение Вольтерра второго рода. Аналогично поступаем и в случае если
, получим интегральное уравнение Вольтерра второго рода. Аналогично поступаем и в случае если 



 , вычислим
, вычислим .
. ,
,  ,
, ,
,  ,
,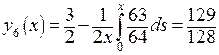 и так далее.
и так далее.
 .
. .
. ,
, 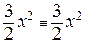 .
.


