Интегральный допплерівський счет

Обратимся теперь к геодезическому режиму работы глобальных систем - фазовым измерением на несущей частоте. В этом случае измеряется не время распространения сигнала от спутника до приемника, а сдвиг фазы колебаний несущей частоты (излучаемой спутником) за это время, но - и это создает главную проблему - не полный сдвиг j_SR, связанный с расстоянием от спутника S к приемнику R, а лишь его дробовая часть, меньшая 2 p. Это та же проблема решения неоднозначности, которая возникает и в наземных фазовых віддалемірах. Сдвиг измеренных фаз реализуется в приемнике как различие фаз между сигналом, принятым от спутника, и опорным сигналом, который генерируется в приемнике. Предположим, что для некоторого фиксированного момента времени мы измерили дробовую часть фазового сдвига Dj. Но, чтобы определить расстояние, нам нужный полный фазовый сдвиг, который равняется

j_SR = 2pN + Dj = wt = 2pf (P/c) (8.3)

где N - неизвестное целое число, f - несущая частота, Р - псевдодальність, что содержит геометрическое расстояние r. С формулы 8.3 легко получить Р, учитывая, что с/f = l (длина волны в вакууме):

Р = lN + l (Dj/2p). (8.4)

Это почти та же псевдодальність, что и при кодовых измерениях, и ее можно представить выражением вида (6.2), но с двумя характерными отличиями. Во-первых, ионосферный член D_и при фазовых измерениях будет иметь другой знак (см. следующий раздел). А во-вторых, величина Dt_г, которая фигурирует в (6.2), будет иметь кое-что другое трактование. При кодовых измерениях она отображает несинхронность хода часов спутника и приемника. При фазовых же измерениях она является следствием несинфазності (неспівпадання начальных фаз) колебаний опорных генераторов спутника и приемника, которую мы будем обозначать через dj. Именно наличие величины dj приводит к тому, что мы и из фазовых измерений получаем псевдодальність. Понятно Dt_г и dj жестко связанные друг с другом (dj = 2pf ·Dt_г), оскільки, внаслідок єдності еталона часу і частоти, “годинник” - це і є генератори коливань.

В литературе часто употребляют выражения “кодовая псевдодальність” и “фазовая псевдодальність”. Добавим им индексы “ к ” и “ ф ” и запишем, с учетом сделанных замечаний, в виде:

Р_к = r + D_т + D_и + сDt_г (8.5)

Р_ф = r + D_т - D_и + c(dj/2pf). (8.6)

Приравнивая (8.4) и (8.6), определим величину Dj/2p, обозначая ее через Ф (вымеренная величина различия фаз, выраженная в частицах цикла - то, что в наземной фазовой віддалеметрії обозначают как DN):

Ф = (r/l) - N + (D_т/ l) - (D_и/l) + (dj/2p). (8.7)

Присутствие неизвестного целого числа N приводит, как уже упоминалось, к проблемы решения неоднозначности.

Обычно в литературе уравнения фазовых измерений используют в виде (8.7).

Если мы каким-то чином определили число N, то можно получить вымеренное значение фазовой псевдодальності Рф. Однако она содержит неизвестную величину dj. Фазовые измерения с двумя приемниками позволяют исключить эту величину, используя так называемый метод фазовых различий.

Метод фазовых различий. Для исключения dj достаточно выполнить измерение не до четверых, как при кодовых измерениях, а только до двух спутников. Величину dj можно представить различием dj_S - dj_R (то есть различием начальных фаз колебаний генераторов на спутнике и в приемнике). Если выполнить наблюдение одного и того же спутника одновременно двумя приемниками, которые разнесены на некоторое расстояние (в пункты А і В), то в различии двух уравнений вида (8.7) исключается величина dj_S для наблюдаемого спутника.

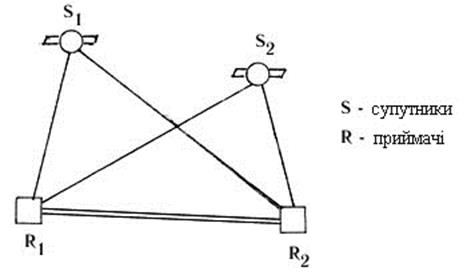
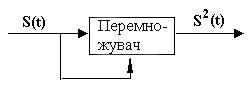
Рис.8.2. Геометрия наблюдений для получения второго фазового различия

Если выполнить теми же приемниками и в ту же эпоху наблюдения второго спутника, то в различии исключается величина dj_S для этого второго спутника. Если теперь составить различие различий - так называемую другу различие (обозначим ее DФ_II), - то исключается величина dj_R для обеих приемников. Геометрия измерений показана на рис.8.2.

Таким образом, во втором различии ликвидируется крупный недостаток одностороннего (беззапитного) фазового метода – неизвестное отличие начальных фаз колебаний на спутнике и в приемнике. Тому спосіб вторых различий есть основным при точных геодезических измерениях.

Однако этот образ не ликвидирует другого крупного недостатка фазовых измерений - необходимости решения неоднозначности.

Отметим, что если повторить вышеописанную процедуру наблюдения двух спутников двумя приемниками в другой момент времени, то есть когда эти спутники займут другое положение, и так же получить другу различие, а потом составить различие вторых различий – третье различие (DФ_III), то неоднозначность, как часто говорят, исключается. На самом деле это не так: неоднозначность в этом случае не исключается, а, так сказать, игнорируется. Суть дела здесь заключается в том, что при образовании третьего различия у нее входят не самые расстояния между спутниками и приемниками, а их прирастить за время перемещения спутников по орбите. Соответственно в третьем различии фигурируют не неизвестные значения N фазовых циклов, а их прирастить DN. Эти приросты могут измеряться за показателями фазометричного устройства при беспрерывному відстежуванні сигнала спутника. Нахождение же целых чисел N (по всем расстояниям), которые имеют порядок»108 и должны быть определенный с точностью до единицы, является исключительно сложной задачей. Полагает, что неоднозначность решена, если точно определенные целые числа No = (NA – NB)^S1 – (NA – NB)^S2, фігуруючі во вторых различиях. Процесс определения No называют инициализацией.

Существует несколько возможных образов определения Nо. Однако в процессе наблюдений оператор не может взнати, решенная ли многозначность - он узнает об этом только после так называемой постобробки, осуществляемой на офисном компьютере, на который перекачиваются все данные, полученные во время работы спутникового приемника.

Фазовые измерения, как основа относительного метода. Если многозначность решена, то другу фазовое различие DФ_II можно перевести в линейную меру (умножением на длину волны l). Это будет второе различие фазовых псевдодальностей, что содержит величины r_А¹, r_В¹, r_А², r_В² - геометрические расстояния от приемников А і В к спутникам 1 и 2. Обозначим указанную другу различие фазовых псевдодальностей через Р¹². Она связана с координатами двух спутников (X₁, Y₁, Z₁), (X₂, Y₂, Z₂) и приемников (Х_А, У_А, ZA), (XB, YB, ZB) соотношением:

Р¹² = [(X_1-XA)² + (Y_1-YA)² + (Z_1-ZA)²]^1/2 -

- [(X_1-XB)² + (Y_1-YB)² + (Z_1-ZB)²]^1/2 -

- [(X_2-XA)² + (Y_2-YB)² + (Z_2-ZB)²]^1/2 +

+ [(X_2-XB)² + (Y_2-YB)² + (Z_2-ZB)²]^1/2 + dD_а¹² (8.8)

где последний член есть “двойное различие атмосферных задержек”, что отображает остаточное влияние атмосферы на трасах распространения сигналов от спутников 1 и 2 к пунктам А і В.

Поскольку координаты спутников известные, то в (8.8) остаются неизвестными координаты пунктов А і В. Если мы выполним на пунктах А і В соответствующие наблюдения (измерение фазовых псевдодальностей Р_ф) до ЧЕТВЕРЫХ спутников (то есть как и в случае кодовых измерений), то получим три независимых уравнения вида (8.8): для Р¹², Р¹³ и Р¹⁴, в которых в качестве неизвестных будут выступать три РАЗЛИЧИЯ одноименных координат пунктов А і В - конечных точек базовой линии: (XA-XB), (YA-YB) и (ZA-ZB), которые и определяются из решения системы уравнений_. Если один из приемников поместить в пункте с известными координатами (что обычно и делают), то за полученными различиями легко находятся координаты второго пункта.

По различиям координат можно вычислить и расстояние между приемниками (длину базы):

АВ = [(XA-XB)² + (YA-YB)² + (ZA-ZB)²]^1/2. (8.9)

Точность фазовых измерений существенным образом превосходит точность кодовых измерений и составляет в среднем [(5-10) + (1-2) D ] мм, где D - длина базы в километрах. По высоте точность выходит кое-что меньше чем в плане.

Восстановление несущей частоты при фазовых измерениях. В подразделе “Кодовые измерения” мы упоминали, что снятие кодовой модуляции возможно, если в приемнике производится копия такого же кода, которым модулируется спутниковый сигнал. Но и при отсутствии копии (например, несущая L2 модулируется только Р- Кодом, которого может не быть в приемнике) задача восстановления несущей решается достаточно просто. Для этого используют квадратування сигнала, который приходит от спутника. Идея образа объясняется на рис.8.3. Кодированный сигнал от спутника разделяется на две части, которые поступают на два входа перемножуючого устройства. На выходе образовывается сигнал, умноженный сам на себя, то есть сведенный в квадрат.

Рис.8.3. К образу квадратування сигнала

 

Пусть сигнал, который проходит с несущей частотой f, имеет вид:

S(t)= А cos (2pf t + j_м) (8.10)

где - индекс “ м ” при начальной фазе j означает манипуляцию на 180^в при изменению символов кода. Используя известное соотношение cos²a = (1/2)(1+cos2a), для исходного сигнала найдем:

S²(t)= A²cos²(2pf t + j_м) = (А^2/2) + (А^2/2)cos(2p2f t + 2j_м). (8.11)

Умножение фазы j_м на 2 снимает фазовую манипуляцию, поскольку перебрасывание на 180^в превращается в изменение на 360 ^об, и на выходе получаем сигнал, который составляется из постоянной составляющей (А^2/2) и немодулированной несущей с амплитудой (А^2/2) и удвоенной частотой 2f, которую легко можно превратить в удобное для фазовых измерений значение.

Интегральный допплерівський счет. Под этим понимается счет периодов допплерівського сдвига частоты Df_д, возникающего через движение спутника, за некоторый промежуток времени Dt = t₂ - t₁, где t₁ и t₂ - моменты начала и конца измерения. Например, можно таким образом подсчитать приросты фазовых циклов при перемещении спутника по орбите с одной точки в другую, а значит, определить и прирост расстояния от приемника. Это дает возможность фиксировать положение спутника в разные эпохи (что напоминает метод третьих различий при фазовых измерениях), или, другими словами, фиксировать последовательные изменения расстояния от наземного приемника к спутнику. А это, в свою очередь, означает, что могут быть определены соответствующие различия расстояний, которые позволяют вычислить положение приемника гиперболической засечкой (см. раздел 6, подраздел «Геометрические принципы позиционирования»).

Почему счет называется интегральным? В приемнике частота f_пр, что приходит = f + Df_д смешивается с частотой fo опорного генератора, как правило, кое-что отличной от частоты f излучаемых спутником колебаний, и различие частот (fo - f_пр), которая называют частотой битья, которое выделяется, интегрируется по времени на интервале (t₂ - t₁). Можно показать, что в результате интеграции определяется различие расстояний от приемника до двух положений спутника, соответствующих моментам t₁ и t₂ (рис.8.4). Фактически здесь происходит то же, что и при интеграции допплерівського сдвига в лазерных интерферометрах при перемещении отражателя, которое определяется как различие двух положений отражателя в начальный и конечный моменты его движения (см. раздел 5).

За допплерівським сдвигом можно найти и скорость изменения расстояния между спутником и приемником (см. раздел 2).

 

Рис.8.4. К допплерівського подсчету фазовых циклов при движении спутника

 

ВОПРОС ДЛЯ САМОКОНТРОЛЯ

 

1. К чему относятся фазовые измерения?

2. Что является вымеренной величиной при фазовых измерениях?

3. Что является основной проблемой при фазовых измерениях?

4. В чем отличие фазовой псевдодальності от кодовой псевдодальності?

5. Что исключается во втором фазовом различии?

6. При решении которых уравнений получают окончательные значения различий координат двух пунктов при фазовых измерениях?

7. Фазовые измерения выполняются на несущей частоте. Что необходимо для снятия кодовой модуляции с целью восстановления несущей?

8. Что исключает первая, вторая, третья фазовые различия на начальной фазе?

9. Спутник движется по почти правильному кругу, в центре которого находится приемник. При перемещении спутника с точки орбиты А в точку В расстояние к приемнику увеличилась на 2,64 г. Почему равняется прирост фазовых циклов на частоте L1?

10. Что позволяет определить число периодов при интегральному допплерівському счету?