Раздел 1. Исторический экскурс в развитие геотроніки

П.В. Мацко, А. Г. Голубев

 

Введение в “Геотронику”

 

Х е р с о н - 2 0 0 6

 

П.В. Мацко, А. Г. Голубев

 

 

Ведение в “Геотроніку”

 

Учебное пособие

 

Tempus Project CD_JEP – 25215 – 2004, GISAU

Геоінформаційні системы и технологии в аграрных университетах

 

Партнеры:

 

1. Херсонский государственный аграрный университет, (UKR)

2. Glasgow Caledonian University, (United Kingdom)

3. University of Gavle, (Sweden)

4. Херсонский государственный университет,(UKR)

 

УДК 528.063:528.232.23:(0.75)

ББК 26.12

 

Допущено Ученым Советом Херсонского ДАУ, как учебное пособие для подготовки магистров и студентов за специальностью «Гидромелиорация», специализации «Геоінформаційні системы и технологии в управлении водными и земельными ресурсами» согласно Проекту CD _ JEP – 25215 – 2004, GISAU (Протокол №10 от 30 июня 2006 г.)

 

Авторы:

Мацко Петр Владимирович – кандидат сельскохозяйственных наук,

доцент кафедры землеустройства и архитектурного проектирования ХДАУ

 

Голубев Анатолий Николаевич – доктор технических наук, профессор

кафедры высшей геодезії Міігаік Рецензенты:

Пєсков І.В. – директор Херсонского научно-исследовательского и проектного института землеустройства

Тягур В.К. – директор Государственного предприятие геодезії, картографии и кадастра «Херсонгеоінформ»

 

ISBN

 

Мацко П.В., Голубев А.М.

Введение в геотроніку: Учебное пособие. - Херсон, ХДУ, 2006.-100с.

 

В учебном пособии рассмотренные физические и геометрические основы электронных методов измерения в геодезії, приведенные примеры применения разных видов віддалемірів и тахеометров для определения расстояний, углов и превышений, а также спутниковых навигационно-геодезических систем для нахождения координате наземных объектов.

Для студентов, магистров и работников аграрных и землеустроительных организаций.

 

 

Координаторы проекта: профессор В.В. Морозов, Украина

профессор Едвін Грей, Объединенное Королевство Великобритании

ВВЕДЕНИЕ

 

Для подготовки специалистов высшей квалификации необходимо обеспечить соответствующий уровень знаний в разных сферах, в которых им необходимо будет работать. В частности, при работе с наземными и спутниковыми радиоэлектронными методами геодезических измерений специалисты повині усвоить теоретические основы и практические навыки таких процессов. Данное учебное пособие предназначено для магистров, аспирантов и студентов, которые изучают геоінформаційні системы и технологии, связанные с получением, накоплением и обработкой геодезической, экологической и другой информации.

Современная полевая геодезическая аппаратура представляет собой объединение электронного или оптико-электронного оборудования и процессора. Обработку измерений выполняют на компьютерах в режиме реального времени или почти одновременно с них выполнением. Практический опыт показывает, что на крупных объектах 60-70% работы выполняется с использованием спутниковых методов, а все другое наземными методами, в основном электронными тахеометрами [2].

Конечным результатом выполнения геодезических и кадастровых работ на данный регион или объект есть геоінформаційні системы. Они включают каталог пунктов геодезической опорной сети, данные кадастровых и землеустроительных работ, а также позволяют вносить и учитывать разного рода информацию. Все этапы создания такой системы, начиная с построения, обновление, усовершенствование опорной геодезической сети и заканчивая обработкам и архивированием результатов кадастровой съемки, нуждаются в высокой квалификации [3,4].

Основным параметром, который определяется при геодезических или топографических роботах, есть координаты пунктов или объектов. С этой целью измерятся линейные и угловые величины с помощью электронных методов в том числе и с использованием навигационно-спутниковых систем. В учебном пособии сделанная попытка даты по возможности простое, короткое и наглядное изложения основных аспектов геотроніки. В отдельных местах для более ясного восприятия основных идей и принципов современной геотроніки опущенные не очень существенные детали. Вопросы, которые детально рассматриваются в общедоступных источниках информации, описанные коротко. Промежуточные математические выкладки не приводятся. Количество структурных схем оборудование сведено к минимуму за счет обобщения схем.

Для более совершенного усвоения дисциплины необходимая практическая работа с современными навигационно-геодезическими спутниковыми системами и электронными тахеометрами в производственных условиях.

 

 

Раздел 2. ФИЗИЧЕСКИЕ ОСНОВЫ ГЕОТРОНІКИ

Рис.2.1. Представление гармонического колебания вектором, который оборачивается

Записав уравнение (2.3) в виде S(t)= А sin , можно дать ему наглядную геометрическую интерпретацию, представивши колебательный процесс в виде вектора, который оборачивается (рис.2.1). Длина (модуль) вектора есть амплитуда А, угол между вектором и осью х – фаза , а угловая скорость обращения (против часовой стрелки) – круговая частота . Фаза – это угловая величина, она измеряется в градусах или радианах. При обращении вектора величиной S(t), что вызывает колебание, есть проекция вектора на ось у.

Ее значение меняется в интервале от + А к – А. Можно наглядно убедиться, что это колебание синусоидальное. Проекция конца вектора на ось в дает точку, которая беспрерывно движется «туда и назад» по оси у. Представим себе, что к этой точке прикрепленное какой-нибудь пишущее устройство (скажем, карандаш или перо с чернилами), а перед ним протягивается бумажная лента с постоянной скоростью. Тогда на ленте будет вычеркиваться синусоида - развертка колебания во времени.

3. При суперпозиции (составлении) двух гармонических колебаний одинаковой частоты результирующее колебание также есть гармоническим и выполняется с той же частотой. Его амплитуда и начальная фаза зависят от соотношения амплитуд и начальных фаз колебаний, которые составляются.

При суперпозиции двух гармонических колебаний с разными частотами результирующее колебание уже не будет гармоническим. Если частоты близкие, то результирующий колебательный процесс называется битьем. При этом амплитуда и фаза результирующего колебания периодически меняются во времени с частотой, которая равняется различию частот начальных колебаний, которые называются частотой битья.

Так, если одновременно взволновать две струны, одна из которых выдает звук с частотой 440 Гц, а другая, немного меньшей длины, - с частотой 444 Гц, причем амплитуда этих звуковых колебаний, то есть их громкость, будет одинаковой, то мы услышим звук со средней частотой 442 Гц, но его громкость периодически будет меняться, становясь то больше, то меньше громкости начальных звуков, и это изменение будет проходить с частотой 4 Гц.

4. Любое негармоническое (сложное), но периодическое колебание с периодом Т можно представить в виде суммы простых гармонических колебаний с частотами, кратными частоте f = 1/Т сложного колебания (ряд Фур”есть). Совокупность составляющих гармонических колебаний называют спектром сложного колебания, а самые составные – гармониками. Гармоники с частотами соответственно f, 2f, 3f и т.д. называются соответственно первой (основной), второй, третьей и т.д. гармониками. Разные гармоники имеют різну амплитуду и фазу. Чем выше номер гармоники, тем обычно меньше ее амплитуда.

Таким образом, любое периодическое колебание имеет дискретный спектр, который составляется из гармоник. Если же колебание непериодическое, то оно представляется не рядом, а интегралом Фурье и имеет сплошной (беспрерывный) спектр, который составляется с бесконечного числа синусоид с беспрерывной последовательностью частот.

5. Колебания, которые распространяются в пространстве или в какой-нибудь среде, называются волнами. Они характеризуются длиной волны , связанной с частотой колебаний f соотношением

 = v/f, (2.5)

где v – скорость распространения колебаний.

6. Частным случаем колебательных процессов есть гармонические колебания напряженность электрического и магнитного полей, которые создают сменное электромагнитное поле. Распространяемое в просторные электромагнитное поле называют электромагнитными волнами. Электромагнитные волны являются поперечными: векторы Е і Н напряженности электрического и магнитного полей взаимно перпендикулярные и лежат в плоскости, перпендикулярной вектору скорости распространения волны.

Электромагнитные волны разделяют по длинам волн на ряд диапазонов, совокупность которых образовывает спектр электромагнитных волн. Большую часть этого спектру занимают радиоволны, длина которых может составлять от 0, 1 мм к больше 100км. Небольшой, но очень важным участком спектру есть оптический диапазон волн. Он делится на три области. Центральная с них – видимая область спектру (видимый свет), что занимает интервал приблизительно от 0,4 мкм (фиолетовый свет) до 0,75 мкм (красный свет). Слева от нее (в бок уменьшения длин волн) находится ультрафиолетовая (УФ) область, а дело (в бок увеличения длин волн) – инфракрасная (ІЧ) область. Ультрафиолетовая и инфракрасная области оптического диапазона спектру невидимые глазом.

7. Электромагнитные волны владеют свойством, которое носит название поляризации. Если колебание вектора Е (то есть напряженности электрического поля) в плоскости, перпендикулярной к направлению распространения волны, происходят в разных, изменяемых случайным чином направлениях в этой плоскости, волна называется неполяризованной. Если же колебание вектора Е происходят только в одном направлении в указанной плоскости, то волна называется линейно поляризованной. Превратить неполяризованную волну в линейно поляризованную можно с помощью специальных устройств – поляризаторов, которые пропускают колебание только одного направления.

8. Уравнение линейно поляризованной монохроматической (то есть рожденной колебанием строго одной частоты) волны, которые распространяется уподовж осы х со скоростью v, имеет вид

S(t,x)= А cos [(t – x/v) +  _об! = А cos (t – kx + _o), (2.6)

где k = /v = 2/ - параметр, который называется волновым числом.

9. Волны одинаковой частоты, которые сохраняют различие фаз постоянной, называются когерентными. При составлении двух когерентных монохроматических волн, линейно поляризованных в одной плоскости, амплитуда суммарной волны будет зависеть от различия фаз волн, которые составляются. Такое взаимодействие волн называется интерференцией. При этом результирующая волна линейно поляризована в той же плоскости, которая и волны, которые составляются.

10. При составлении двух когерентных монохроматических волн, линейно поляризованных во взаимно перпендикулярных плоскостях, интерференции не происходит. В общем случае (то есть при разных амплитудах волн и произвольном сдвиге фаз между ними) проекция конца электрического вектора на плоскость, перпендикулярную напрямую распространения, описывает эллипс. Такая волна называется эллиптически поляризованной. Если амплитуды волн, которые составляются, уровне, то вид эллипса зависит только от различия фаз (этих волн. Это иллюстрируется в таблица.2.1.

Таблица 2.1.

 

Из таблицы видно, что при различия фаз 90° и 270° эллипс превращается в круг и волна называется поляризованной по кругу или циркулярно поляризованной. При различия фаз 0° или 180° эллипс вырождается в прямую линию и волна будет линейная поляризованной. Таким образом, линейная и круговая поляризация являются отдельными случаями эллиптической поляризации.

 

ЗАПИТАНННЯ ДЛЯ САМОКОНТРОЛЯ:

1. Есть ли периодические колебания гармоническими?

2. Каким отношением объединенная частота f с периодом Т?

3. Которые три параметра полностью характеризуют гармоничные колебания?

4. Что имеет дискретный спектр?

5. Какой наиболее общий случай поляризации электромагнитных волн?

6. Что такое когерентные волны?

7. Как связанная длина волны λ с частотой и скоростью распространения колебаний?

8. Как называется величина 2π/λ?

9. Как называется колебания, у которого какой-нибудь параметр меняется во времени?

10. Как называется результат составления двух когерентных волн, линейно поляризованных в одной плоскости?

 

2.2. Преобразование гармонических колебаний

Модуляция. Модуляцией называется изменение параметров колебания во времени по определенному закону. Согласно тому, какой параметр модулируется (А,  или _о), различают амплитудную модуляцию (АМ), частотную (ЧМ) и фазовую (ФМ). В світловіддалемірах иногда используют еще один вид модуляции – поляризационную (ПМ), при которой меняется состояние поляризации световых колебаний. Колебание, параметр которого модулируется, называется несущим колебанием, а его частота f = /2 – несущей частотой. Модуляция заключается в том, что выбранный параметр подвергается действию модулюючого колебание, который задает закон изменения параметра. В простейшем случае модуляция осуществляется по гармоническому закону. При этом модулированный параметр P представляется в виде

P(t)= Р_о + P cos t = Р_о (1 + m cos t), (2.7)

где Р_о – соответствующий параметр не модулированного колебания,

P – амплитуда изменения параметра,  = 2F – круговая частота модуляции (F – частота модуляции, то есть частота модулюючого колебание). Величину m = P/Po называют коэффициентом модуляции. Частота модуляции всегда намного меньше несущей частоты, то есть F f (соответственно   ).

В наземных віддалемірних устройствах наиболее часто применяется амплитудная модуляция по гармоническому закону. Рассмотрим этот случай подробнее.

Пусть не модулированное (несущее) колебание имеет вид (2.4), в котором для простоты положим начальную фазу _в = 0:

S = А_о cos t. (2.8)

При гармонической АМ амплитуда, в соответствии с (2.7), меняется во времени согласно закону

А(t)= Ат + А cos t = Ат (1 + m cos t) (2.9)

 

 

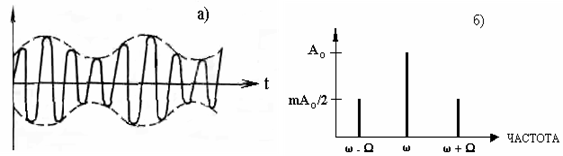
Рис.2.2. а) Ам-Колебание, в котором амплитуда меняется по гармоническому закону,

б) Частотный спектр Ам-Колебание.

и уравнение АМ - колебание будет

SAM = Ат (1 + m cos t) cos t. (2.10).

График такого колебания показан выше (рис.2.2,а). Применивши к (2.10) известную из тригонометрии формулу для произведения косинусов:

cos · cos = (1/2) [cos ( - ) + cos ( + )] (2.10)

можно представить в виде

SAM = А_оcos t + (mao /2)cos ( - )t + (mao /2)cos ( + )t. (2.11)

Обсудим выражения (2.10) и (2.11). Формула (2.10) показывает, что Ам- Колебания –это колебания одной частоты  (несущей), но со сменной амплитудой Ao(1 + mcos t), величина которой меняется во времени с частотой модуляции . Формула же (2.11) говорит о том, что Ам- Колебание составляется с трех гармонических составляющих с частотами , - и + и постоянными амплитудами (А_о, mao/2 и mAо/2 соответственно). Вопрос «что же есть Ам- Колебание на самом деле?» некорректное: оба представления эквивалентные. В одних случаях целесообразно использовать запись (2.10), в других – (2.11). Выражение (2.11) показывает частотный спектр Ам- Колебание (рис.2.2., б). Частоты - и + называются боковыми частотами. Таким образом, амплитудно-модулированное колебание состоит в общем случая с несущей частоты и двух боковых частот.

Интересным частным случаем есть битье, о котором упоминалось выше – результат составления двух близких частот ₁ и ₂. Битье – это тоже Ам- Колебание, но его спектр составляется с двух этих частот.

Кроме гармонической модуляции, часто используется модуляция по прямоугольному закону, когда значение модулированного параметра скачкообразно меняется от Р1 к Р2 и спустя некоторое время – назад, и этот процесс повторяется через одинаковые или разные интервалы времени. Модуляцию по прямоугольному закону называют манипуляцией. Манипуляция фазы используется, например, в глобальных спутниковых навигационных системах.

Демодуляция. Демодуляцией или детектуванням называется процесс, в результате которого со сложного модулированного колебания выделяется модулююче колебание. Это процедура, обратная модуляции. Существуют детекторы АМ-, ЧМ - и Фм- Колебаний. Обычно ЧМ - и ФМ колебания превратят в Ам- Колебание, которое детектується наиболее просто. Детектування Ам- Колебание являются нелинейной операцией, в процессе которой происходит перемножения этого колебания или на несущее колебание, или именно на себя. Первый вариант называют синхронным детектуванням, второй – квадратичным детектуванням. В обеих случаях в результате перемножения выходит сумма слагаемых (спектр), один из которых будет колебанием модулюючої частоты, которое выделяют с помощью соответствующего фильтру, который пропускает только эту частоту.

Гетеродинування. Так называют операцию преобразования частоты колебания с целью получить колебание другой частоты. Обычно эта операция используется для понижения частоты. Для осуществления гетеродинування начальное колебание частоты f смешивается в радиотехническом смесителе с колебанием, частота которого отличается от f на небольшую величину f. Это колебание получают от гетеродина – вспомогательного генератора. Под змішенням обычно понимается перемножения колебаний. В результате перемножения образовывается спектр частот, который содержит, в частности, колебание разностной частоты f, которое можно выделить с помощью соответствующего фильтру. Таким образом, колебание высокой частоты f превратится у колебания низкой частоты f. При этом фаза низкочастотного колебания равняется различию фаз змішуваних колебаний.

Гетеродинування широко используется в геодезических фазовых віддалемірах, в которых возникает задача измерения различия фаз двух высокочастотных сигналов. Пусть есть два колебания одинаковой высокой частоты f:

S₁ = A₁ cos (2f t + ₁) (2.12)

S₂ = А₂ cos (2f t + ₂) (2.13)

различие фаз которых

 = ₂ - ₁ (2.14)

необходимо измерить. Смешавши каждое из этих колебаний с колебаниями гетеродина частоты f_г

S_г = B cos (2f_г t + _г) (2.15)

в смесителях См1 и См 2 (рис.2.3) и направивши исходные сигналы смесителей в усилителе низкой частоты 1 и 2, получим на выходах усилителей колебания разностной частоты

f - fг = f вида

s₁ = C₁ cos [(2 f t + (₁ - _г)] (2.16)

s₂ = C₂ cos [(2 f t + (₂ - _г)]. (2.17)

Различие фаз этих колебаний

(₂ - _г) – (₁ - _г) = ₂ - ₁ =  (2.18)

то есть различие фаз колебаний низкой (разностной) частоты f равняется различию фаз начальных колебаний высокой частоты f, или, другими словами, при гетеродинуванні фазовые соотношения не меняются. Этот весьма важный вывод говорит о том, что измерение различия фаз двух колебаний высокой частоты можно, применивши гетеродинуванні, заменить измерениям различия фаз двух низкочастотных колебаний, которая выполняется технически проще и точнее.

Рис.2.3. Гетеродинная схема измерения различия фаз

Корреляционная обработка негармонических сигналов. Понятие «корреляционная обработка» применяется к широкополосным сигналам, то есть к сигналам, володіючих широким спектром. Целью корреляционной обработки есть измерения времени задержки между двумя одинаковыми, но сдвинутыми по времени широкополосными сигналами. Если есть два таких сигнала: S1 (t) и S2 (t + ), где  - временная задержка второго сигнала относительно первого, то вводится понятия корреляционной функции этих сигналов К_1.2, равной

К_1.2 =  S₁(t)· S₂ (t + ), (2.19)

где угловые дужки означают усреднение за большой промежуток времени – такой, который больше периода самой низкочастотной составляющей спектру сигналов S₁ и S₂. Значение корреляционной функции приобретают на выходе корелятора – устройства, которое реализовывает операцию (2.19) перемножение и усреднение при подачи сигналов S₁ и S₂ на его входы. Корреляционная функция К_1.2 имеет один резко выраженный максимум при  = 0. Итак, если принудительно менять задержку  к получению максимума исходного сигнала корелятора и измерить нужно величину изменения, мы тем самым определим эту задержку. По сути дела, это компенсационный образ, в котором индикатором момента компенсации задержки служит максимум корреляционной функции. Положительным качеством корреляционного метода является малое влияние шумов, сопровождающих сигналы S₁ и S₂, на результат измерений. Корреляционная обработка сигналов используется в радіоінтерферометрії со сверхдлинной базой (РНДБ) и при так называемых кодовых измерениях в глобальных спутниковых системах.

ВОПРОС ДЛЯ САМОКОНТРОЛЯ:

Лазеры. Эффект Допплера.

Лазер – это источник оптического излучения с высокой степенью когерентности. В самом общем значении термин«когерентность» означает «согласованность». Свет называется когерентным, если все атомы вещества выпускают световые волны, которые имеют строго одинаковую амплитуду, частоту, фазу, поляризацию и направление распространения. Такого идеально когерентного источника не существует, но лазер есть наилучшим к нему приближением.

Любой лазер составляется с трех основных элементов (рис.2.4): активного среды (твердого, редкого или газообразного), источника накачки и открытого резонатора, создаваемого двумя параллельными зеркалами, между которыми помещается активная среда. Одно из зеркал делается частично прозрачным для выхода излучения из лазера.

.Принцип работы лазера сводится к следующему. Активная среда, получая энергию от источника накачки, переходит в так называемое состояние с инверсной обитаемостью энергетических уровней – возбужденное состояние, при котор число атомов вещества, «перекинутых» на более высокий энергетический уровень, становится больше числа атомов, которые остались на нижнем (основном) энергетическом уровне. Это состояние есть неустойчивому: любой из атомов, которые оказались на верхнему уровне может непроизвольно перейти назад на основной уровень, выпуская при этом квант света (фотон) определенной

 

Рис.2.4. Принципиальная схема лазера

 

частоты, зависимой от различия энергий уровней. Так и происходит, причем моменты рождения разных фотонов, инициированных переходами тех или других атомов, случаю, не слаженные друг с другом, фотоны при этом разлетаются в разных направлениях, направляясь «кто куда». Такое излучение называется спонтанным (невольным), и оно некогерентное.

И вот здесь вступает в игру оптический резонатор. Спонтанные фотоны, которые родились в направлении оси резонатора, пройдут вдоль него сравнительно большой путь, много раз циркулируя между преломляющими зеркалами. При этом возникает очень важное обстоятельство. Она заключается в том, что циркулирующие фотоны, взаимодействуя на своем пути с атомами, которые накопились на верхнем энергетическом уровне, инициируют их переход на нижний уровень с выпуском фотонов. Поскольку эти переходы возникают не случайно, а натянуто, под действием циркулирующих вдоль оси резонатора фотонов, то фотоны, которые рождаются при этих переходах будут точной копией того фотона, который «вынуждает», – они будут иметь ту же энергию, тот же направление движения и другие абсолютно идентичные характеристики. Возникает могущественная лавина слаженных фотонов. Такое излучение называется (в отличие от спонтанного) вынужденным (а также стимулирующим или индуцированным) и есть, как легко понять, когерентным. То обстоятельство, которое в лазере имеет место стимулирующее излучение, отображено в самом слове «лазер» - это слово (LASER) является аббревиатурой, составленной из первых букв английской фразы Light Amplification Stimulated Emission Radiation – «усиление света с помощью стимулирующего излучения». В этой фразе, правда, говорится об усилении света, тогда как лазер – это генератор света, однако это не имеет принципиального значения, поскольку любой усилитель можно, как известно, превратить в генератор введением цепи обратной связи из выхода на вход усилителя. Такой цепью и есть зеркала резонатора (усилителем служит возбужденная активная среда). После каждого двойного прохода длины резонатора часть излучения выходит из лазера через полупрозрачное зеркало.

Лазер может генерировать не любые длины волн , а только такие, которые составляются целое число раз q на двойной длине резонатора 2L, то есть удовлетворяют уму резонанса:

2L = q . (2.20).

Эти резонансные длины волн называются продольными модами, и если в полосу усиления активного среды попадается много таких длин волн, то они генерируются одновременно, то есть в спектре излучения лазера может содержаться много продольных мод, отдаленных друг от друга по частоте на одинаковый интервал  = с_р/2L, где с_р – скорость света в резонаторе. Такие лазеры называются багатомодовими. Специальными методами селекции можно выделить только одну моду, и тогда лазер называют одномодовим или одночастотным.

Лазерное излучение владеет следующими свойствами, которые отличают его от излучения всех других источников:

- высокой степенью пространственной и временной когерентности;

- (как следствие) высокой степенью монохроматичности, то есть сосредоточено в очень узком спектральном интервале (идеально монохроматического источника не существует, но лазер есть наилучшим к нему приближением);

- чрезвычайной вузьконаправленістю (малой шириной пучка);

- высокой спектральной плотностью мощности (плотность мощности – это мощность, которая приходится на единицу площади, например, на 1 см² ; спектральная плотность мощности – плотность мощности, отнесенная единичного спектрального интервала, например, до 1 мкм).

В зависимости от вида активного среды различают твердо тільні лазеры, жидкостные (лазеры на растворах органических фарбників), газу и полупроводнику.

Твердотільні лазеры. К ним относятся лазеры на рубине, на неодимовом стекле и на натрий-алюминиевом гранате. Они работают в импульсном режиме, излучая короткие оптические импульсы большой мощности (лазер на гранате может работать и в беспрерывном режиме). С них в геодезії в данное время используются могущественные пікосекундні импульсные лазеры на гранате с длиной волны излучения 1,06 мкм - в лазерных віддалемірах для измерения расстояний к ШСЗ временным методом, о чем уже упоминалось выше. В последнее время осваивается применения лазеров на титан-сапфире, от которых можно получать импульсы фемтосекундного диапазона (1 фс = 10-15с) продолжительностью в сотне и десятки фемтосекунд.

Газовые лазеры генерируют беспрерывное излучение. Кроме уже упоминавшегося неоновый^-неонового-гелий-неонового (Не-Ne) лазера, который используется в наземных світловіддалемірах и излучаемого красный свет с длиной волны 0,63 мкм, в двохвильових світловіддалемірах (см. раздел 8) могут использоваться гелій-кадмієвий (Не-Сd) лазер с длиной волны 0,44 мкм (синий свет) и аргоновый (Аr) лазер, который может одновременно генерировать излучение на двух длинах волн: 0,46 мкм (синий свет) и 0,51 мкм (зеленый свет). Газовые лазеры имеют самую большую степень монохроматичности излучения.

Лазеры на фарбниках владеют замечательным свойством – возможностью перестройки длины волны в широком диапазоне, но геодезического применения они пока не получили.

Полупроводниковые лазеры составляют особый класс лазеров, принимая во внимание их весьма специфические свойства, они широко используются в современных наземных світловіддалемірах и электронных тахеометрах. Одной из наиболее привлекательных их качеств есть очень малые размеры (меньше 1см) и масса. Полупроводниковый лазер на арсениде галлия, чаще всего уживается в віддалемірній технике, является лазерным диодом, выполненным в виде кристалла, составленного с двух «половинок» с разными типами проводимости – электронной (n- проводимость) идырчатой (p- проводимость). Между ними образовывается зона, которая называется p-n- переходом. Если на эти «половинки» представить постоянное напряжение питания (подключивши положительный полюс к p- области), то в зоне p-n- перехода образовываются фотоны и оттуда выходит излучение. Так получается світлодіод, но его излучение некогерентное. Чтобы превратить світлодіод на лазерный диод, надо отполировать торцу грани кристалла, которые будут служить зеркалами резонатора, и увеличат плотность тока через диод. Тогда излучение становится когерентным – мы получаем полупроводниковый лазер.

Кроме малых габаритов, такой лазер владеет еще одним ценным свойством – возможностью внутренней модуляции излучения. То есть если в віддалемірі источником излучения служит полупроводниковый лазер, то модулятора, как отдельного устройства не надо – достаточно представить напряжение питания на лазерный диод, как сменную модулюючу напругу от генератора и излучения, которые выходит из диода будет модулированным. При этом возможная модуляция с очень высокой частотой - до 1 Ггц.

Эффект Допплера. Этот эффект заключается в том, что при сближении или отдалении излучателя (передатчика) и приемника частота колебаний, которая принимается, будет отличаться от частоты излучаемых колебаний. При этом безразлично, что именно движется – излучатель или приемник; важно их относительное движение, то есть изменение расстояния между ними. (Это справедливо в случае пренебрежения релятивистскими, то есть связанными с теорией относительности, эффектами, которыми во всех что интересуют нас случаях можно пренебрегать через малую частицу скорости движения в сравнении со скоростью света). Если, скажем, излучатель отдаляется от недвижимого приемника, то последний будет принимать в единицу времени меньше волн в сравнении со случаем неизменного расстояния между излучателем и приемником. То есть длины волн увеличиваются, а частота соответственно уменьшается. В случае приближения излучателя к приемнику картина меняется на обратную – в единицу времени воспринимается больше волн, то есть волны становятся менее короткими и частота увеличивается. Если передатчик, установленный, например, на спутнике что движется, излучает радиоволне с неизменной частотой f, то воспринимаемая приемником частота равная

f_пр = f [1  (V/v)], (2.21)

где V – радиальная скорость спутника (проекция вектора скорости на направление «спутник – приемник»), v – скорость электромагнитных волн (в среде). Знак в дужках зависит от направления движения.

Таким образом, частота, которая принимается, отличается от излучаемой на величину

f_д = f_пр – f  = f(V/v) (2.22)

званую допплерівським сдвигом (или сдвигом) частоты, или просто допплерівською частотой.

Кроме «спутникового случая» с излучением радиоволн, допплерівський сдвиг имеет место и в оптическом диапазоне, в частности, при отражении света от зеркала, которое движется, при работе лазерных интерферометров перемещений. В этом случае свет от лазера с частотой  (этой буквой принято обозначать частоту в оптическом диапазоне), прежде чем попасть в приемник, проходит двойное расстояние – к зеркалу (отражателя), что движется, и назад, и формула (2.22) приобретает вид:

_д =  (2V/v) (2.23)

где V – скорость движения отражателя, v – скорость света в воздухе. Поскольку /v = 1/, то (2.23) можно переписать в виде:

_д = 2V/. (2.24)

ВОПРОС ДЛЯ САМОКОНТРОЛЯ:

 

1. Что такое лазер?

2. С чего составляется лазер?

3. Источник накачки перевело активную среду в состояние с инверсной обитаемостью энергетических уровней. При переходе атомов назад на нижний уровень выпускаются фотоны, которые создают спонтанное излучение. Которые из фотонов инициируют преобразование спонтанного излучения в стимулированное?

4. В чем состоит роль резонатора в лазере?

5. Ширина полосы усиления активного среды гелий-неонового лазера составляет 1500Мгц. Сколько продольных мод содержится в спектре излучения, если длина резонатора равняется 30см? Скорость света в резонаторе принять равной 300000000 м/с?

6. Что представляет собой монохроматическое излучение?

7. Что используется для измерения расстояний к ШСЗ?

8. В результате чего образовывается допплерівський сдвиг?

9. Подвижный передатчик, установленный на спутнике, излучает радиоволны с частотой 1500Мгц. Почему равняется допплерівський сдвиг частоты (в килогерцах), которая принимается недвижимым наземным приемником, если радиальная скорость спутника в (десять в степени шесть) раз меньше скорости радиоволн?

10. He-Ne лазер интерферометра излучает свет с длиной волны 0,6 мкм. С какой скоростью (в м/с) движется отражатель интерферометра, если допплерівський сдвиг оптической частоты составляет 1Мгц?

 

 

Рис.3.1. Общая схема измерения расстояний с помощью электромагнитных волн

дистанции, которые измеряется. Для этого один и тот же сигнал от передатчика разделяется на две части и направляется на приемник одновременно по двум разным путям: непосредственно (без выхода на дистанцию) и через дистанцию, которая измерится (рис.3.1).

Первый путь называют опорным каналом или трактом, а сигнал, который идет по нему - опорным сигналом. Второй путь образовывает дистанционный (информационный) канал, и соответственно сигнал, который приходит от отражателя называют дистанционным или информационным сигналом.

В приемнике (под приемником на рис.3.1 понимается приемо-измерительное устройство) осуществляется сравнения опорного и информационного сигналов по выбранному параметру, или, другими словами, измеряется их отличие по этому параметру, которое и содержит информацию о расстоянии, которое измеряется. Выбор параметра определяет метод измерения расстояния. Такими параметрами чаще всего есть:

<