Раздел 2. Физические основы геотроніки

Электромагнитные колебания и волны.

Основные понятия и определения

1. Среди множества колебательных процессов особое место занимают периодические колебания, для которых выполняется равенство

S(t)= S(t + NT), (2.1)

где S(t) – величина, которая колеблется, t – время, N – любое целое число, Т – некоторый якнайменший конечный промежуток времени, через которое повторяются значения всех физических величин, которые характеризуют колебательное движение. Этот промежуток времени называется периодом колебания. Обратная периоду величина

f = 1/T (2.2)

выражает число колебаний в единицу времени и называется частотой. Частота измеряется в герцах. 1 герц (Гц) – это одно колебание в секунду. Уживаются также следующие единицы частоты:

килогерц (кГц) - 103 Гц

мегагерц (Мгц) - 106 Гц

гігагерц (ГГц) - 109 Гц

терагерц (ТГц) - 1012 Гц.

2. Простейшим, но практически самым важным случаем периодических колебаний есть гармонические (синусоидальные) колебания, описываемые уравнениям вида

S(t)= А sin (t + _o) (2.3)

или

S(t)= А cos (t + _o) (2.4)

(косинусоїда – это та же синусоида, только сдвинутая на четверть периода). Величина А называется амплитудой колебания  = 2f – угловой или круговой частотой  _об! начальной фазой. Эти три параметра полностью характеризуют гармоническое колебание. Аргумент синуса или косинуса в (2.3) или (2.4), то есть величину  = (t + _o), называют текущей фазой, мгновенной фазой или просто фазой колебания. Таким образом, фаза и начальная фаза – это резни вещи. Начальная фаза – это фаза колебания в момент t = 0

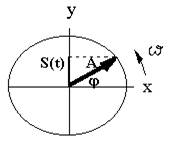
Рис.2.1. Представление гармонического колебания вектором, который оборачивается

Записав уравнение (2.3) в виде S(t)= А sin , можно дать ему наглядную геометрическую интерпретацию, представивши колебательный процесс в виде вектора, который оборачивается (рис.2.1). Длина (модуль) вектора есть амплитуда А, угол между вектором и осью х – фаза , а угловая скорость обращения (против часовой стрелки) – круговая частота . Фаза – это угловая величина, она измеряется в градусах или радианах. При обращении вектора величиной S(t), что вызывает колебание, есть проекция вектора на ось у.

Ее значение меняется в интервале от + А к – А. Можно наглядно убедиться, что это колебание синусоидальное. Проекция конца вектора на ось в дает точку, которая беспрерывно движется «туда и назад» по оси у. Представим себе, что к этой точке прикрепленное какой-нибудь пишущее устройство (скажем, карандаш или перо с чернилами), а перед ним протягивается бумажная лента с постоянной скоростью. Тогда на ленте будет вычеркиваться синусоида - развертка колебания во времени.

3. При суперпозиции (составлении) двух гармонических колебаний одинаковой частоты результирующее колебание также есть гармоническим и выполняется с той же частотой. Его амплитуда и начальная фаза зависят от соотношения амплитуд и начальных фаз колебаний, которые составляются.

При суперпозиции двух гармонических колебаний с разными частотами результирующее колебание уже не будет гармоническим. Если частоты близкие, то результирующий колебательный процесс называется битьем. При этом амплитуда и фаза результирующего колебания периодически меняются во времени с частотой, которая равняется различию частот начальных колебаний, которые называются частотой битья.

Так, если одновременно взволновать две струны, одна из которых выдает звук с частотой 440 Гц, а другая, немного меньшей длины, - с частотой 444 Гц, причем амплитуда этих звуковых колебаний, то есть их громкость, будет одинаковой, то мы услышим звук со средней частотой 442 Гц, но его громкость периодически будет меняться, становясь то больше, то меньше громкости начальных звуков, и это изменение будет проходить с частотой 4 Гц.

4. Любое негармоническое (сложное), но периодическое колебание с периодом Т можно представить в виде суммы простых гармонических колебаний с частотами, кратными частоте f = 1/Т сложного колебания (ряд Фур”есть). Совокупность составляющих гармонических колебаний называют спектром сложного колебания, а самые составные – гармониками. Гармоники с частотами соответственно f, 2f, 3f и т.д. называются соответственно первой (основной), второй, третьей и т.д. гармониками. Разные гармоники имеют різну амплитуду и фазу. Чем выше номер гармоники, тем обычно меньше ее амплитуда.

Таким образом, любое периодическое колебание имеет дискретный спектр, который составляется из гармоник. Если же колебание непериодическое, то оно представляется не рядом, а интегралом Фурье и имеет сплошной (беспрерывный) спектр, который составляется с бесконечного числа синусоид с беспрерывной последовательностью частот.

5. Колебания, которые распространяются в пространстве или в какой-нибудь среде, называются волнами. Они характеризуются длиной волны , связанной с частотой колебаний f соотношением

 = v/f, (2.5)

где v – скорость распространения колебаний.

6. Частным случаем колебательных процессов есть гармонические колебания напряженность электрического и магнитного полей, которые создают сменное электромагнитное поле. Распространяемое в просторные электромагнитное поле называют электромагнитными волнами. Электромагнитные волны являются поперечными: векторы Е і Н напряженности электрического и магнитного полей взаимно перпендикулярные и лежат в плоскости, перпендикулярной вектору скорости распространения волны.

Электромагнитные волны разделяют по длинам волн на ряд диапазонов, совокупность которых образовывает спектр электромагнитных волн. Большую часть этого спектру занимают радиоволны, длина которых может составлять от 0, 1 мм к больше 100км. Небольшой, но очень важным участком спектру есть оптический диапазон волн. Он делится на три области. Центральная с них – видимая область спектру (видимый свет), что занимает интервал приблизительно от 0,4 мкм (фиолетовый свет) до 0,75 мкм (красный свет). Слева от нее (в бок уменьшения длин волн) находится ультрафиолетовая (УФ) область, а дело (в бок увеличения длин волн) – инфракрасная (ІЧ) область. Ультрафиолетовая и инфракрасная области оптического диапазона спектру невидимые глазом.

7. Электромагнитные волны владеют свойством, которое носит название поляризации. Если колебание вектора Е (то есть напряженности электрического поля) в плоскости, перпендикулярной к направлению распространения волны, происходят в разных, изменяемых случайным чином направлениях в этой плоскости, волна называется неполяризованной. Если же колебание вектора Е происходят только в одном направлении в указанной плоскости, то волна называется линейно поляризованной. Превратить неполяризованную волну в линейно поляризованную можно с помощью специальных устройств – поляризаторов, которые пропускают колебание только одного направления.

8. Уравнение линейно поляризованной монохроматической (то есть рожденной колебанием строго одной частоты) волны, которые распространяется уподовж осы х со скоростью v, имеет вид

S(t,x)= А cos [(t – x/v) +  _об! = А cos (t – kx + _o), (2.6)

где k = /v = 2/ - параметр, который называется волновым числом.

9. Волны одинаковой частоты, которые сохраняют различие фаз постоянной, называются когерентными. При составлении двух когерентных монохроматических волн, линейно поляризованных в одной плоскости, амплитуда суммарной волны будет зависеть от различия фаз волн, которые составляются. Такое взаимодействие волн называется интерференцией. При этом результирующая волна линейно поляризована в той же плоскости, которая и волны, которые составляются.

10. При составлении двух когерентных монохроматических волн, линейно поляризованных во взаимно перпендикулярных плоскостях, интерференции не происходит. В общем случае (то есть при разных амплитудах волн и произвольном сдвиге фаз между ними) проекция конца электрического вектора на плоскость, перпендикулярную напрямую распространения, описывает эллипс. Такая волна называется эллиптически поляризованной. Если амплитуды волн, которые составляются, уровне, то вид эллипса зависит только от различия фаз (этих волн. Это иллюстрируется в таблица.2.1.

Таблица 2.1.

 

Из таблицы видно, что при различия фаз 90° и 270° эллипс превращается в круг и волна называется поляризованной по кругу или циркулярно поляризованной. При различия фаз 0° или 180° эллипс вырождается в прямую линию и волна будет линейная поляризованной. Таким образом, линейная и круговая поляризация являются отдельными случаями эллиптической поляризации.

 

ЗАПИТАНННЯ ДЛЯ САМОКОНТРОЛЯ:

1. Есть ли периодические колебания гармоническими?

2. Каким отношением объединенная частота f с периодом Т?

3. Которые три параметра полностью характеризуют гармоничные колебания?

4. Что имеет дискретный спектр?

5. Какой наиболее общий случай поляризации электромагнитных волн?

6. Что такое когерентные волны?

7. Как связанная длина волны λ с частотой и скоростью распространения колебаний?

8. Как называется величина 2π/λ?

9. Как называется колебания, у которого какой-нибудь параметр меняется во времени?

10. Как называется результат составления двух когерентных волн, линейно поляризованных в одной плоскости?

 

2.2. Преобразование гармонических колебаний

Модуляция. Модуляцией называется изменение параметров колебания во времени по определенному закону. Согласно тому, какой параметр модулируется (А,  или _о), различают амплитудную модуляцию (АМ), частотную (ЧМ) и фазовую (ФМ). В світловіддалемірах иногда используют еще один вид модуляции – поляризационную (ПМ), при которой меняется состояние поляризации световых колебаний. Колебание, параметр которого модулируется, называется несущим колебанием, а его частота f = /2 – несущей частотой. Модуляция заключается в том, что выбранный параметр подвергается действию модулюючого колебание, который задает закон изменения параметра. В простейшем случае модуляция осуществляется по гармоническому закону. При этом модулированный параметр P представляется в виде

P(t)= Р_о + P cos t = Р_о (1 + m cos t), (2.7)

где Р_о – соответствующий параметр не модулированного колебания,

P – амплитуда изменения параметра,  = 2F – круговая частота модуляции (F – частота модуляции, то есть частота модулюючого колебание). Величину m = P/Po называют коэффициентом модуляции. Частота модуляции всегда намного меньше несущей частоты, то есть F f (соответственно   ).

В наземных віддалемірних устройствах наиболее часто применяется амплитудная модуляция по гармоническому закону. Рассмотрим этот случай подробнее.

Пусть не модулированное (несущее) колебание имеет вид (2.4), в котором для простоты положим начальную фазу _в = 0:

S = А_о cos t. (2.8)

При гармонической АМ амплитуда, в соответствии с (2.7), меняется во времени согласно закону

А(t)= Ат + А cos t = Ат (1 + m cos t) (2.9)

 

 

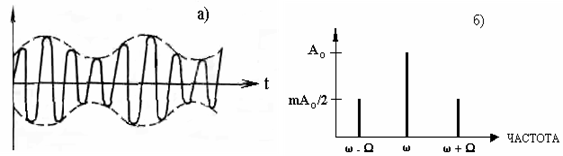
Рис.2.2. а) Ам-Колебание, в котором амплитуда меняется по гармоническому закону,

б) Частотный спектр Ам-Колебание.

и уравнение АМ - колебание будет

SAM = Ат (1 + m cos t) cos t. (2.10).

График такого колебания показан выше (рис.2.2,а). Применивши к (2.10) известную из тригонометрии формулу для произведения косинусов:

cos · cos = (1/2) [cos ( - ) + cos ( + )] (2.10)

можно представить в виде

SAM = А_оcos t + (mao /2)cos ( - )t + (mao /2)cos ( + )t. (2.11)

Обсудим выражения (2.10) и (2.11). Формула (2.10) показывает, что Ам- Колебания –это колебания одной частоты  (несущей), но со сменной амплитудой Ao(1 + mcos t), величина которой меняется во времени с частотой модуляции . Формула же (2.11) говорит о том, что Ам- Колебание составляется с трех гармонических составляющих с частотами , - и + и постоянными амплитудами (А_о, mao/2 и mAо/2 соответственно). Вопрос «что же есть Ам- Колебание на самом деле?» некорректное: оба представления эквивалентные. В одних случаях целесообразно использовать запись (2.10), в других – (2.11). Выражение (2.11) показывает частотный спектр Ам- Колебание (рис.2.2., б). Частоты - и + называются боковыми частотами. Таким образом, амплитудно-модулированное колебание состоит в общем случая с несущей частоты и двух боковых частот.

Интересным частным случаем есть битье, о котором упоминалось выше – результат составления двух близких частот ₁ и ₂. Битье – это тоже Ам- Колебание, но его спектр составляется с двух этих частот.

Кроме гармонической модуляции, часто используется модуляция по прямоугольному закону, когда значение модулированного параметра скачкообразно меняется от Р1 к Р2 и спустя некоторое время – назад, и этот процесс повторяется через одинаковые или разные интервалы времени. Модуляцию по прямоугольному закону называют манипуляцией. Манипуляция фазы используется, например, в глобальных спутниковых навигационных системах.

Демодуляция. Демодуляцией или детектуванням называется процесс, в результате которого со сложного модулированного колебания выделяется модулююче колебание. Это процедура, обратная модуляции. Существуют детекторы АМ-, ЧМ - и Фм- Колебаний. Обычно ЧМ - и ФМ колебания превратят в Ам- Колебание, которое детектується наиболее просто. Детектування Ам- Колебание являются нелинейной операцией, в процессе которой происходит перемножения этого колебания или на несущее колебание, или именно на себя. Первый вариант называют синхронным детектуванням, второй – квадратичным детектуванням. В обеих случаях в результате перемножения выходит сумма слагаемых (спектр), один из которых будет колебанием модулюючої частоты, которое выделяют с помощью соответствующего фильтру, который пропускает только эту частоту.

Гетеродинування. Так называют операцию преобразования частоты колебания с целью получить колебание другой частоты. Обычно эта операция используется для понижения частоты. Для осуществления гетеродинування начальное колебание частоты f смешивается в радиотехническом смесителе с колебанием, частота которого отличается от f на небольшую величину f. Это колебание получают от гетеродина – вспомогательного генератора. Под змішенням обычно понимается перемножения колебаний. В результате перемножения образовывается спектр частот, который содержит, в частности, колебание разностной частоты f, которое можно выделить с помощью соответствующего фильтру. Таким образом, колебание высокой частоты f превратится у колебания низкой частоты f. При этом фаза низкочастотного колебания равняется различию фаз змішуваних колебаний.

Гетеродинування широко используется в геодезических фазовых віддалемірах, в которых возникает задача измерения различия фаз двух высокочастотных сигналов. Пусть есть два колебания одинаковой высокой частоты f:

S₁ = A₁ cos (2f t + ₁) (2.12)

S₂ = А₂ cos (2f t + ₂) (2.13)

различие фаз которых

 = ₂ - ₁ (2.14)

необходимо измерить. Смешавши каждое из этих колебаний с колебаниями гетеродина частоты f_г

S_г = B cos (2f_г t + _г) (2.15)

в смесителях См1 и См 2 (рис.2.3) и направивши исходные сигналы смесителей в усилителе низкой частоты 1 и 2, получим на выходах усилителей колебания разностной частоты

f - fг = f вида

s₁ = C₁ cos [(2 f t + (₁ - _г)] (2.16)

s₂ = C₂ cos [(2 f t + (₂ - _г)]. (2.17)

Различие фаз этих колебаний

(₂ - _г) – (₁ - _г) = ₂ - ₁ =  (2.18)

то есть различие фаз колебаний низкой (разностной) частоты f равняется различию фаз начальных колебаний высокой частоты f, или, другими словами, при гетеродинуванні фазовые соотношения не меняются. Этот весьма важный вывод говорит о том, что измерение различия фаз двух колебаний высокой частоты можно, применивши гетеродинуванні, заменить измерениям различия фаз двух низкочастотных колебаний, которая выполняется технически проще и точнее.

Рис.2.3. Гетеродинная схема измерения различия фаз

Корреляционная обработка негармонических сигналов. Понятие «корреляционная обработка» применяется к широкополосным сигналам, то есть к сигналам, володіючих широким спектром. Целью корреляционной обработки есть измерения времени задержки между двумя одинаковыми, но сдвинутыми по времени широкополосными сигналами. Если есть два таких сигнала: S1 (t) и S2 (t + ), где  - временная задержка второго сигнала относительно первого, то вводится понятия корреляционной функции этих сигналов К_1.2, равной

К_1.2 =  S₁(t)· S₂ (t + ), (2.19)

где угловые дужки означают усреднение за большой промежуток времени – такой, который больше периода самой низкочастотной составляющей спектру сигналов S₁ и S₂. Значение корреляционной функции приобретают на выходе корелятора – устройства, которое реализовывает операцию (2.19) перемножение и усреднение при подачи сигналов S₁ и S₂ на его входы. Корреляционная функция К_1.2 имеет один резко выраженный максимум при  = 0. Итак, если принудительно менять задержку  к получению максимума исходного сигнала корелятора и измерить нужно величину изменения, мы тем самым определим эту задержку. По сути дела, это компенсационный образ, в котором индикатором момента компенсации задержки служит максимум корреляционной функции. Положительным качеством корреляционного метода является малое влияние шумов, сопровождающих сигналы S₁ и S₂, на результат измерений. Корреляционная обработка сигналов используется в радіоінтерферометрії со сверхдлинной базой (РНДБ) и при так называемых кодовых измерениях в глобальных спутниковых системах.

ВОПРОС ДЛЯ САМОКОНТРОЛЯ: