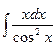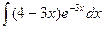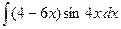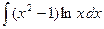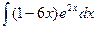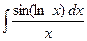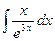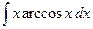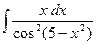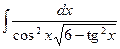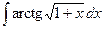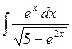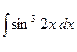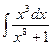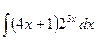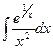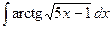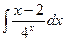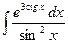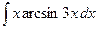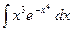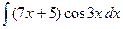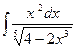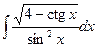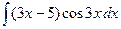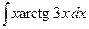Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегральное исчисление функций одной независимой переменнойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
СОДЕРЖАНИЕ
Пояснительная записка Цель преподавания математики в вузе – ознакомить студентов с основами математического аппарата, необходимого для решения теоретических и практических задач; привить студентам умение самостоятельно изучать учебную литературу по математике и ее приложениям; развить логическое мышление и повысить общий уровень математической культуры; выработать навыки математического исследования прикладных вопросов и умение перевести задачу на математический язык. Настоящее пособие для студентов очно-заочной и ускоренной формы обучения всех технических специальностей содержит методические указания и контрольные задания по курсам интегрального исчисления, дифференциального исчисления функций нескольких переменных, дифференциальным уравнениям. Перед выполнением контрольной работы студент должен изучить соответствующие разделы курса по учебной литературе, рекомендуемой в данном пособии. Каждая задача контрольной работы содержит по 30 вариантов. Номер варианта расчетной работы определяется по последним двум цифрам номера зачетной книжки студента и соответствует этим цифрам, если они образуют число от 01 до 30. Если же число больше 30, то номер варианта равен остатку после деления этого числа на тридцать. Если же в остатке получен ноль, тогда ваш вариант 30.
Интегральное исчисление функций одной независимой переменной Неопределенный интеграл Рассмотрим основные методы отыскания неопределенного интеграла. 1. Непосредственное интегрирование. Данный метод основан на применении свойств неопределенного интеграла и таблицы основных интегралов.
Свойства неопределенного интеграла (правила интегрирования) 1. 2. 3. 4. 5. 6. Если
Таблица основных интегралов
Пример 1.1. Найти интеграл Решение. Используя свойства 4 и 5, получаем
Пользуясь таблицей интегралов, получаем
Пример 1.2. Найти интеграл Решение.
Свойство 6 позволяет расширить таблицу основных интегралов с помощью приема внесения функции под знак дифференциала. Пример 1.3. Решение. Этот интеграл можно привести к табличному интегралу, преобразовав его следующим образом:
Теперь переменной интегрирования служит выражение
Пример 1.4. Решение. Поступая так же, как и в примере 1.3, имеем:
Пример 1.5. Решение. Выражение
2. Замена переменной в неопределенном интеграле. Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов: 1.
2.
Пример 1.6. Вычислить интеграл: Решение. Воспользуемся подстановкой
Ответ нужно выразить через старую переменную
Пример 1.7. Решение. Положим
Замечание 1.1. Если интеграл
где
Пример 1.8. Решение. Положим
Пример 1.9. Решение. Для того чтобы свести интеграл к табличному, разделим числитель и знаменатель подынтегрального выражения на
Дополним теперь таблицу основных интегралов следующими формулами:
Пример 1.10. Решение. Выполним подстановку
Пример 1.11. Решение. Преобразуя знаменатель дроби, получим
Пример 1.12. Решение. Положим
3. Интегрирование по частям. Интегрированием по частям называют нахождение интеграла по формуле
где Замечание 1.2. Для интегралов вида Пример 1.13. Решение. Положим в (1.1)
Пример 1.14. Решение. Положим в (1.1)
Определенный интеграл Приложение определенного интеграла Приведем некоторые приложения определенного интеграла. Дифференциальные уравнения Рассмотрим основные виды дифференциальных уравнений первого порядка. Однородные уравнения Функция
В частности, функция Дифференциальное уравнение вида
Вводя новую искомую функцию При решении однородных уравнений переходить к виду (3.1) необязательно. Можно сразу делать подстановку
Пример 3.3. Решить уравнение: Решение. Разделив обе части уравнения на
Сделаем подстановку
Разделяем переменные
Интегрируем
Пусть теперь Пример 3.4. Решить уравнение: Решение. Сделаем подстановку
Разделим переменные
отсюда интегрированием находим
делая обратную подстановку, в итоге получаем:
Уравнение Бернулли Уравнение Бернулли имеет вид
где С помощью замены переменной Пример 3.7. Решить уравнение Бернулли
Решение. Умножим обе части уравнения на
Сделаем замену
общее решение которого
Отсюда получаем общий интеграл исходного уравнения:
Замечание 3.2. Уравнение Бернулли может быть проинтегрировано также методом вариации постоянной, как и линейное уравнение, и с помощью подстановки Пример 3.8. Решить уравнение Бернулли
Решение. Ищем общее решение уравнения (3.10) в виде
или
Функцию
разделяем переменные
интегрируем:
следовательно, общее решение уравнения (4.10) будет
Укажем некоторые видыдифференциальных уравнений, допускающие понижение порядка. 1. Уравнение вида 2. Уравнение не содержит искомой функции и ее производной до порядка
Порядок такого уравнения можно понизить на
Из последнего уравнения определяем 3. Уравнение не содержит независимой переменной:
Подстановка
Подставив эти выражения вместо Пример 3.9. Найти общее решение уравнения Решение. Интегрируя последовательно данное уравнение, имеем
Пример 3.10. Решить уравнение Решение. Данное уравнение явно не содержит
Делая обратную замену, получаем Пример 3.11. Решить дифференциальное уравнение Решение. Данное уравнение явно не содержит
Рассмотрим два случая: 1. 2. интегрируем обе части последнего уравнения, получаем
Учитывая, что
После интегрирования получаем общий интеграл данного дифференциального уравнения:
Особое внимание следует уделить линейнымдифференциальным уравнениям второго порядка с постоянными коэффициентами:
где Рассмотрим линейное однородное уравнение второго порядка с постоянными коэффициентами:
Уравнение вида
называется характеристическим уравнением для уравнения (3.14). Вид общего решения уравнения (3.14) зависит от корней характеристического уравнения. Обозначим эти корни через Если корни характеристического уравнения вещественные и
Если корни уравнения (3.15) вещественные и равные, то есть
Если корни характеристического уравнения комплексные
Пример 3.12. Найти общее решение уравнение
Решение. Составим характеристическое уравнение
Пример 3.13. Найти общее решение уравнение Решение. Составим характеристическое уравнение
Пример 3.14. Найти общее решение уравнение Решение. Характеристическое уравнение
Рассмотрим линейное неоднородное уравнение с постоянными коэффициентами (3.13). Теорема 4.1. Общее решение неоднородного уравнения (3.13) равно сумме общего решения соответствующего однородного уравнения (3.14) и какого-либо частного решения неоднородного уравнения:
В случае, когда правая часть уравнения (3.13) имеет вид
где Сводная таблица видов частных решений Контрольная работа №4. «Интегральное исчисление функции одной независимой переменной» Задача 1. Вычислить неопределенные интегралы
Задача 2. Вычислить неопределенные интегралы
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.163.15 (0.015 с.) |

 .
. .
. .
. , где
, где  - постоянная.
- постоянная. .
. и
и  , то
, то 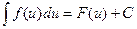

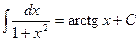
 при
при 







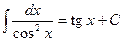




 .
. .
. .
. .
.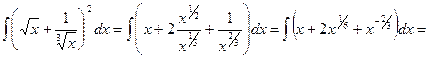
 .
. .
.
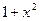 и относительно этой переменной получим интеграл от степенной функции. Следовательно,
и относительно этой переменной получим интеграл от степенной функции. Следовательно, .
. .
. .
. .
. можно записать как
можно записать как  , поэтому
, поэтому .
.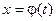 , где
, где  - монотонная, непрерывно дифференцируемая функции новой переменной
- монотонная, непрерывно дифференцируемая функции новой переменной  . Формула замены переменой в этом случае имеет вид
. Формула замены переменой в этом случае имеет вид ;
;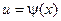 , где
, где  - новая переменная. Формула замены переменной при такой подстановке:
- новая переменная. Формула замены переменной при такой подстановке: .
. .
. , то есть
, то есть 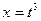 . Найдем дифференциал
. Найдем дифференциал  . Отсюда имеем
. Отсюда имеем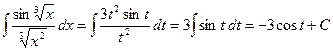 .
. . Подставляя в результат интегрирования
. Подставляя в результат интегрирования  .
.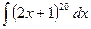 .
.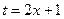 , тогда
, тогда  , откуда
, откуда  . После подстановки в исходный интеграл получим
. После подстановки в исходный интеграл получим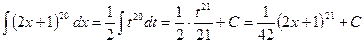 .
. является табличным, то интеграл
является табличным, то интеграл  можно найти с помощью подстановки
можно найти с помощью подстановки  . Фактически саму подстановку можно не производить. Здесь достаточно принять во внимание, что
. Фактически саму подстановку можно не производить. Здесь достаточно принять во внимание, что  . Таким образом,
. Таким образом, ,
, - первообразная для
- первообразная для  . Например,
. Например, ,
,  ,
, и т.д.
и т.д. .
.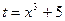 , тогда
, тогда  , откуда
, откуда  . После подстановки в исходный интеграл получаем
. После подстановки в исходный интеграл получаем .
. , где
, где  .
.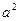 :
: .
.
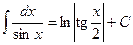
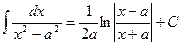
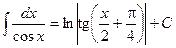



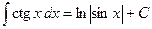
 .
. , тогда
, тогда  ,
,  и
и  . Значит,
. Значит, .
. .
. . Воспользуемся подстановкой
. Воспользуемся подстановкой  , тогда
, тогда  . Отсюда
. Отсюда .
. .
. , тогда
, тогда  и
и .
. ,
,
 - непрерывно дифференцируемые функции от
- непрерывно дифференцируемые функции от  ,
,  ,
,  , где
, где  - многочлен, в (1.1) за
- многочлен, в (1.1) за  ,
,  ,
,  за
за  принимают выражение
принимают выражение 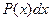 .
. 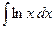 .
. ,
, 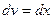 , тогда
, тогда  ,
, 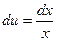 . Используя формулу интегрирования по частям, получаем
. Используя формулу интегрирования по частям, получаем .
. .
. ,
, 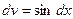 , тогда
, тогда 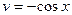 ,
,  . Используя формулу интегрирования по частям, получаем
. Используя формулу интегрирования по частям, получаем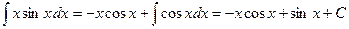 .
. называется однородной функцией своих аргументов измерения
называется однородной функцией своих аргументов измерения  , если справедливо тождество.
, если справедливо тождество. .
.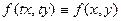 для любых
для любых  .
. называется однородным относительно
называется однородным относительно  , если
, если  .
.
 , уравнение (3.1) можно привести к уравнению с разделяющимися переменными.
, уравнение (3.1) можно привести к уравнению с разделяющимися переменными.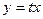 ,
,  .
. .
. , имеем
, имеем , или
, или  .
. ,
,  ,
, 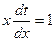 ,
,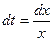 ,
,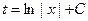 ,
, ,
, 
 . Непосредственной подстановкой убеждаемся, что
. Непосредственной подстановкой убеждаемся, что  .
. .
. ,
,  ,
,  ,
, ,
,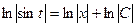 ,
,  ,
,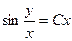 .
. ,
,
 (при
(при  и
и  это уравнение является линейным).
это уравнение является линейным). уравнение Бернулли приводится к линейному уравнению и интегрируется как линейное.
уравнение Бернулли приводится к линейному уравнению и интегрируется как линейное. ,
,
 :
: .
. , тогда
, тогда  . После подстановки последнее уравнение обратится в линейное уравнение:
. После подстановки последнее уравнение обратится в линейное уравнение: ,
, .
. .
. .
. .
.
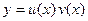 ,
,  . Подставляя выражения для
. Подставляя выражения для  в (3.10), получим
в (3.10), получим ,
, .
.
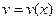 находим из условия
находим из условия ,
, 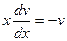 ,
,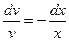 ,
, .
. , откуда
, откуда  . Возьмем, например, частное решение
. Возьмем, например, частное решение  , подставляя его в (3.11), получаем уравнение
, подставляя его в (3.11), получаем уравнение  . Данное уравнение является уравнением с разделяющимися переменным, из которого, разделяя переменные и интегрируя, найдем
. Данное уравнение является уравнением с разделяющимися переменным, из которого, разделяя переменные и интегрируя, найдем ;
;  ,
,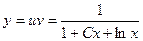 .
. . После
. После  включительно:
включительно:
 единиц заменой
единиц заменой  . Тогда Уравнение (3.12) примет вид
. Тогда Уравнение (3.12) примет вид
 , а затем находим
, а затем находим 
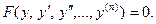
 позволяет понизить порядок уравнения на единицу. При этом
позволяет понизить порядок уравнения на единицу. При этом  рассматривается как новая функция от
рассматривается как новая функция от  . Все производные
. Все производные  выражаются через производные от новой неизвестной функции
выражаются через производные от новой неизвестной функции  ,
,  и т.д.
и т.д. -го порядка.
-го порядка. .
. ,
,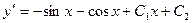 ,
,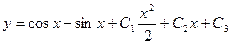 .
.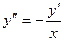 .
.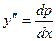 , тогда получим
, тогда получим  - уравнение с разделяющимися переменными.
- уравнение с разделяющимися переменными. ,
,  ,
,  .
.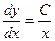 , откуда
, откуда  .
. .
. ,
,  , тогда получим
, тогда получим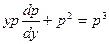 ,
,  .
. ,
,  ,
,  - особое решение.
- особое решение. ;
;  ;
;  ;
; ,
,  ,
, 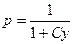 .
. ,
, ,
,  .
. .
. ,
,
 - постоянные величины.
- постоянные величины.

 .
. , то общее решение уравнения (3.13) имеет вид
, то общее решение уравнения (3.13) имеет вид .
.
 , то общее решение уравнения (3.14) имеет вид:
, то общее решение уравнения (3.14) имеет вид: .
.
 , то общее решение уравнения (3.14) имеет вид:
, то общее решение уравнения (3.14) имеет вид: .
.
 .
. . Находим корни
. Находим корни  ,
,  . Применяя формулу (3.16), запишем общее решение уравнения:
. Применяя формулу (3.16), запишем общее решение уравнения: .
. .
. . Корни уравнения
. Корни уравнения  . Применяя формулу (3.17), запишем общее решение уравнения:
. Применяя формулу (3.17), запишем общее решение уравнения: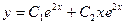 .
. .
.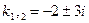 . В силу формулы (3.18) общее решение уравнения имеет вид:
. В силу формулы (3.18) общее решение уравнения имеет вид: .
. .
. ,
, и
и  - многочлены степени
- многочлены степени  соответственно, частное решение неоднородного уравнения находится так называемым методом подбора. Вид частного решения следует искать в одной из следующих форм.
соответственно, частное решение неоднородного уравнения находится так называемым методом подбора. Вид частного решения следует искать в одной из следующих форм.