
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное исчисление функций одного переменногоСодержание книги
Поиск на нашем сайте
Глава VII Дифференциальное исчисление функций одного переменного П. 1 Определение производной Определение 1. Пусть функция
Геометрический смысл производной Заметим, что в – угол наклона хорды
Физический (механический) смысл производной Пусть точка движется по закону Таким образом, значение производной перемещения в момент времени Рассмотрим функцию Тогда Пример. Рассмотрим функцию Тогда Пример. Рассмотрим функцию Тогда
Пример. Рассмотрим функцию Найдем значение производной данной функции при Так как
функция
Определение 2. Пусть функция
Теорема 1. Критерий дифференцируемости функции в точке Для того, чтобы функция Доказательство: Необходимость. Пусть Найдем отношение приращения функции к приращению аргумента: С другой стороны, этот предел равен
Достаточность. Пусть существует Полагая,
Замечание. Процесс нахождения производной функции в точке называют дифференцированием. Замечание. Производную Таким образом, Теорема 2. Если функция Доказательство: Пусть функция Замечание. Обратное утверждение неверно. Например, функция
Определение 3. Говорят, что функция
Дифференцирование функций, заданных неявно Определение 2. Пусть для каждой точки и Определение 3. Придавая постоянные значения числу z ( Для того, чтобы продифференцировать неявно заданную функцию Формулы дифференцирования
1)
Доказательство:
Рассмотрим функцию
2) Доказательство:
Рассмотрим функцию 3) Доказательство:
Рассмотрим функцию
4)
Доказательство:
Рассмотрим функцию
5) Доказательство:
Рассмотрим функцию
6)
Доказательство:
Рассмотрим функцию
7)
Доказательство:
Рассмотрим функцию
8) Доказательство:
Рассмотрим функцию 9) 10) 11)
П. 3 Дифференциал функции
Пусть функция Определение 1. Дифференциалом функции
Теорема 1. Теорема Ферма Пусть функция Доказательство: Для определенности пусть Так как
Замечание. Теорема Ферма является необходимым условием экстремума. Обратное утверждение, вообще говоря, неверно.
Пример. Рассмотрим функцию Пример. Для квадратичной функции
Теорема 2. Теорема Ролля Пусть Доказательство: Так как функция Пусть 1. Если 2. Если Замечание. Все условия данной теоремы существенны. (рисунки – 3 шт.).
Теорема 2. Теорема Лагранжа Пусть функция Доказательство:
Введем вспомогательную функцию
Тогда
Замечание. Геометрический смысл теоремы: $ точка x, в которой касательная к графику функции имеет такой же наклон, как и хорда, соединяющая точки
Замечание. Теорема Лагранжа является обобщением теоремы Ролля. Теорема 3. Теорема Коши Пусть функции Доказательство: Докажем сначала, что Введем вспомогательную функцию
Тогда
Таким образом,
Замечание. Теорема Коши является наиболее общей теоремой, т.е. теорема Ролля и Лагранжа являются следствиями из теоремы Коши.
Теорема 4. Теорема Лопиталя Пусть функции Доказательство:
Рассмотрим окрестность
Перейдем к пределу при
Замечание. Если
Пример. Вычислим
Пример. Вычислим Замечание. Теорема Лопиталя сформулирована для неопределенности типа
Пример. Вычислим
П. 7 Формула Тейлора
Можно заметить, что чем больше производных совпадают у двух функций в некоторой точке, тем лучше эти функции аппроксимируют (приближают) друг друга в окрестности этой точки. Нас будет интересовать приближение функции в окрестности одной точки с помощью многочленов. Рассмотрим многочлен степени
Определение 1. Функция Определение 2. Выражение вида
Теорема 1. Если функция Доказательство:
Пусть имеет место формула Тейлора для функции
Используя правило Лопиталя, покажем, что тогда =…=
Замечание. В формуле Тейлора первое слагаемое называют главной частью функции, а второе – оста т очный член функции Если Остаточный член в виде Формула Тейлора используется для того, чтобы приблизить функцию многочленом Пример. Разложим многочлен
Асимптоты
Определение 6. Прямая
Теорема 6. Функция Доказательство:
Необходимость. Пусть функция Перейдем к пределу при
Рассмотрим
Достаточность. Пусть
Замечание. Если Замечание. Если на отрезке
Глава VII Дифференциальное исчисление функций одного переменного
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 356; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.242.223 (0.013 с.) |

 определена в некоторой окрестности точки
определена в некоторой окрестности точки  . Тогда если существует предел отношения приращения функции
. Тогда если существует предел отношения приращения функции  к приращению аргумента
к приращению аргумента  при
при  , то он называется производной функции
, то он называется производной функции  в точке
в точке  .
. , где
, где  , а б - угла наклона касательной, проведенной к графику функции
, а б - угла наклона касательной, проведенной к графику функции  . Если
. Если  . Это значит, что
. Это значит, что  . Таким образом, значение производной функции
. Таким образом, значение производной функции  . Вычислим среднюю скорость движения за момент времени
. Вычислим среднюю скорость движения за момент времени  :
:  . Устремим
. Устремим  , тогда
, тогда  .
. равно мгновенной скорости движения точки в данный момент времени.
равно мгновенной скорости движения точки в данный момент времени. .
. .
. .
. .
. .
.
 .
.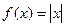 .
. .
. ,
, , то производная этой функции в точке
, то производная этой функции в точке  является производной исходной функции при
является производной исходной функции при  .
. определена в некоторой окрестности точки
определена в некоторой окрестности точки  , тогда
, тогда  , где
, где  и
и  .
. была дифференцируема в точке
была дифференцируема в точке  .
. . Перейдем к пределу:
. Перейдем к пределу:  .
. , т.е.
, т.е.  .
. . Это значит, что:
. Это значит, что:  . Умножив последнее равенство на Dx, получим:
. Умножив последнее равенство на Dx, получим:  .
. , мы получили определение дифференцируемости. ■
, мы получили определение дифференцируемости. ■ называют правой производной функции
называют правой производной функции  - левой производной.
- левой производной. , причем
, причем 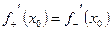 .
. . Значит,
. Значит,  непрерывна в точке
непрерывна в точке  , но не дифференцируема в этой точке.
, но не дифференцируема в этой точке. , если она дифференцируема в каждой внутренней точке этого отрезка.
, если она дифференцируема в каждой внутренней точке этого отрезка. плоскости
плоскости  существует единственное число
существует единственное число  . Тогда говорят, что на плоскости задана функция
. Тогда говорят, что на плоскости задана функция  двух переменных
двух переменных  и
и  .
. ), получим уравнения, задающие линии в пространстве. Тогда функция
), получим уравнения, задающие линии в пространстве. Тогда функция 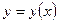 , заданная уравнением
, заданная уравнением  , называется заданной неявно.
, называется заданной неявно. , то уравнение
, то уравнение  задает окружности с центром на оси
задает окружности с центром на оси  . Найдем производную функции
. Найдем производную функции  .
.
 . Так как
. Так как , то
, то
 . Для доказательства этой формулы мы воспользовались следствием 4 из второго замечательного предела. ■
. Для доказательства этой формулы мы воспользовались следствием 4 из второго замечательного предела. ■ .
. . Так как
. Так как 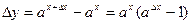 , то
, то  . Для доказательства этой формулы мы воспользовались следствием 4 из второго замечательного предела. ■
. Для доказательства этой формулы мы воспользовались следствием 4 из второго замечательного предела. ■ .
. . Так как
. Так как  , то
, то . Для доказательства этой формулы мы воспользовались следствием 3 из второго замечательного предела. ■
. Для доказательства этой формулы мы воспользовались следствием 3 из второго замечательного предела. ■ .
. . Так как
. Так как , то
, то  . Для доказательства этой формулы мы воспользовались первым замечательным пределом и непрерывностью функции
. Для доказательства этой формулы мы воспользовались первым замечательным пределом и непрерывностью функции  . ■
. ■ .
. , то
, то . Для доказательства этой формулы мы воспользовались первым замечательным пределом и непрерывностью функции
. Для доказательства этой формулы мы воспользовались первым замечательным пределом и непрерывностью функции  .
. . Используя правила дифференцирования, получим
. Используя правила дифференцирования, получим . ■
. ■ .
. . Используя правила дифференцирования, получим
. Используя правила дифференцирования, получим
 ■
■ .
. . Используя правила дифференцирования, получим
. Используя правила дифференцирования, получим  . ■
. ■ .
. .
. .
. дифференцируема в точке
дифференцируема в точке  , тогда
, тогда  ,
,  называется главная часть приращения и обозначается.
называется главная часть приращения и обозначается.  . Дифференциалом аргумента (вне зависимости от переменной) называют его приращение
. Дифференциалом аргумента (вне зависимости от переменной) называют его приращение  . Таким образом, дифференциал функции равен
. Таким образом, дифференциал функции равен  . Тогда производная функции равна
. Тогда производная функции равна 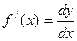 .
. , причем
, причем  - точка локального экстремума функции
- точка локального экстремума функции  .
. . Рассмотрим производную
. Рассмотрим производную  .
. , то получим, что
, то получим, что  . ■
. ■ . Производная функции
. Производная функции  равна нулю при
равна нулю при  , но эта точка не является точкой экстремума функции.
, но эта точка не является точкой экстремума функции. абсцисса
абсцисса  - экстремумом функции. Исходя из этого, найдем координаты
- экстремумом функции. Исходя из этого, найдем координаты  вершины параболы. Так как
вершины параболы. Так как  и
и  ,
, 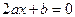 , то
, то 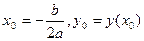 .
. и дифференцируема на интервале
и дифференцируема на интервале  , причем
, причем  .Тогда найдется точка
.Тогда найдется точка  .
. , а
, а  . Тогда возможны два случая:
. Тогда возможны два случая: , то
, то  . Тогда
. Тогда  .
. , то пусть
, то пусть  . Это значит, что на интервале
. Это значит, что на интервале  функция
функция  . ■
. ■ .
. так, чтобы функция
так, чтобы функция  удовлетворяла теореме Ролля, т.е.
удовлетворяла теореме Ролля, т.е.  :
: ,
,  ,
, .
. ,
, ,
, 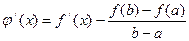 . Таким образом,
. Таким образом,  ■
■ и
и  . (Рисунок)
. (Рисунок) .
. непрерывны на отрезке
непрерывны на отрезке  . Тогда
. Тогда 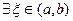 такая, что
такая, что  .
. . Функция
. Функция  . Отсюда
. Отсюда  .
. так, чтобы она удовлетворяла условиям теоремы Ролля.
так, чтобы она удовлетворяла условиям теоремы Ролля. .
. . Отсюда
. Отсюда .
. или
или  . ■
. ■ точки
точки 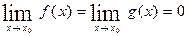 ,
,  и
и  . Тогда
. Тогда  .
. . Тогда, начиная с некоторого номера N, члены последовательности попадают в эту окрестность. Тогда, так как
. Тогда, начиная с некоторого номера N, члены последовательности попадают в эту окрестность. Тогда, так как  и
и  , то функции
, то функции  ,
,  . Тогда на отрезке
. Тогда на отрезке  данные функции непрерывны и дифференцируемы на интервале
данные функции непрерывны и дифференцируемы на интервале  . Таким образом, выполняются все условия теоремы Коши. Это значит, что
. Таким образом, выполняются все условия теоремы Коши. Это значит, что , где
, где  , или
, или  .
. :
:  ,
, не существует, то из этого не следует, что не существует
не существует, то из этого не следует, что не существует  .
.
 , но
, но  не существует.
не существует. . Применяя правило Лопиталя, получим
. Применяя правило Лопиталя, получим 
 .
. и имеет место для неопределенностей типа
и имеет место для неопределенностей типа 
 . Для этого прологарифмируем функцию
. Для этого прологарифмируем функцию  . Тогда
. Тогда 
 . Следовательно,
. Следовательно,  .
. :
:  . Заметим, что
. Заметим, что  . Так как
. Так как  , то
, то . Аналогично получим
. Аналогично получим  ,
,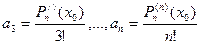 .
. в точке
в точке 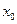 на интервале
на интервале  .
.

 называется формулой Тейлора для функции
называется формулой Тейлора для функции  , причем
, причем ,
,  ,
,  . Обозначим
. Обозначим .
. . Так как
. Так как 
 , …,
, …,  ,
,  ,
, =
= . ■
. ■ , то формулу Тейлора
, то формулу Тейлора  для функции
для функции  называют остаточным членом в форме Пеано.
называют остаточным членом в форме Пеано.

 по степеням
по степеням  . Для этого найдем коэффициенты разложения:
. Для этого найдем коэффициенты разложения: 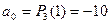 ,
,  ,
, ,
,  . Тогда
. Тогда .
. называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции  , если
, если  - БМФ при
- БМФ при  , т.е.
, т.е.  .
. , а
, а  .
. . Разделим обе части равенства на
. Разделим обе части равенства на  .
. :
: . Следовательно,
. Следовательно, 
 . Перейдем к пределу:
. Перейдем к пределу: .
. :
:
 где
где 
 =>
=> 
 , то говорят, что функция имеет горизонтальную асимптоту
, то говорят, что функция имеет горизонтальную асимптоту  .
. называется вертикальной асимптотой.
называется вертикальной асимптотой.


