
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 2. О единственности разложения функции по формуле ТейлораСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Если функция Доказательство:
Вычтем одно из другого и получим:
Пусть
Замечание. Обратное утверждение, вообще говоря, неверно, т.е. можно найти такие две функции, которые будут иметь одинаковые разложения по формуле Тейлора в некоторой окрестности точки
Разложение основных элементарных функций по формуле Маклорена
1. Функция 2. Функция Аналогично имеют место следующие разложения: 3. 4. 5.
П. 8 Исследование функции и построение графиков
Определение 1. Точка Пример. Рассмотрим функцию водная Пусть
Аналогично рассуждая, получим, что если
Теорема 1. Если 1) если 2) если 3) если Доказательство: Пусть Пусть
Пример. Исследуем функцию
Понятие выпуклости и вогнутости функции
Определение 2. Функция
Пример. Покажем, что функция Рассмотрим
Таким образом,
Определение 3. Функция
Определение 4. Функция
Замечание. Выпуклость функции называют выпуклостью вниз, а вогнутость – выпуклостью вверх.
Теорема 2. Критерий выпуклости Для того, чтобы функция Доказательство:
Необходимость. Пусть
Таким образом, Достаточность. Пусть
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.117.172 (0.008 с.) |

 в некоторой окрестности точки
в некоторой окрестности точки  имеет разложение по формуле Тейлора, то это разложение единственно.
имеет разложение по формуле Тейлора, то это разложение единственно. . Пусть функция
. Пусть функция  ,
,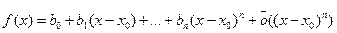 .
. .
. , тогда
, тогда 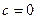 . Разделим полученное равенство
. Разделим полученное равенство  на
на 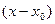 . Получим
. Получим 
 . Тогда при
. Тогда при 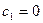 . Рассуждая аналогично, получим
. Рассуждая аналогично, получим  . Следовательно,
. Следовательно,  . Таким образом, разложения совпадают. ■
. Таким образом, разложения совпадают. ■ в окрестности точки
в окрестности точки  имеет разложение
имеет разложение  , так как
, так как  . Данное разложение позволяет вычислить
. Данное разложение позволяет вычислить 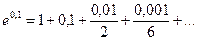 .
. в окрестности точки
в окрестности точки 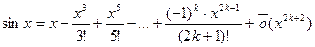 , так как
, так как  .
. ;
;
 ;
; .
. равна нулю или не существует, называется критической точкой функции
равна нулю или не существует, называется критической точкой функции  .
. . Произ-
. Произ- функции не существует в точке
функции не существует в точке  . Следовательно,
. Следовательно, 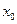 является критической точкой функции
является критической точкой функции 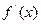 меняет знак с “+” на “-”, то
меняет знак с “+” на “-”, то  , то
, то  , то неравенство
, то неравенство 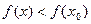 имеет место для всех
имеет место для всех  из левой полуокрестности точки
из левой полуокрестности точки  , то неравенство
, то неравенство 
 , то
, то  то:
то: то
то 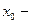 точка минимума;
точка минимума; то
то 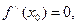 то требуется дополнительное исследование.
то требуется дополнительное исследование. . Тогда существует производная
. Тогда существует производная  .
.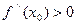 . Тогда
. Тогда  возрастает в окрестности
возрастает в окрестности  . Следовательно,
. Следовательно,  на экстремум. Найдем производную функции:
на экстремум. Найдем производную функции:
 . Таким образом,
. Таким образом,  - критические точки данной функции. Так как
- критические точки данной функции. Так как  , то
, то  ,
,  . По теореме точка
. По теореме точка  требует исследования знака первой производной:
требует исследования знака первой производной:  при всех
при всех  , то по теореме
, то по теореме  - точка минимума.
- точка минимума. , если
, если 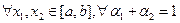 выполняется неравенство Йенсена
выполняется неравенство Йенсена 
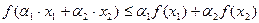 .
. является выпуклой на всей числовой оси. Пусть
является выпуклой на всей числовой оси. Пусть  .
.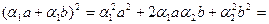


 .
. .
. касательная, проведенная к графику функции
касательная, проведенная к графику функции  и
и  . (Рисунок)
. (Рисунок) .
. , дифференцируемая на интервале
, дифференцируемая на интервале  была выпуклой на нем, необходимо и достаточно, чтобы
была выпуклой на нем, необходимо и достаточно, чтобы 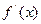 монотонно возрастала на этом интервале. При этом строгому возрастанию
монотонно возрастала на этом интервале. При этом строгому возрастанию 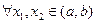 ,
,  ,
, 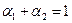 ,
,  ;
; ,
,  ;
;  ,
,  . Так как
. Так как  то
то  ,
, ,
, ,
, ,
, ,
, ,
, . По теореме Лагранжа
. По теореме Лагранжа 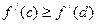 , где
, где  .
.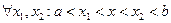 ,
,  , так как
, так как ,
,  ■
■


