
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел функции на бесконечностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
§ Число A называется пределом функции Кратко: Если Бесконечно большие функции § Функция
Иными словами, такая функция f (x) является неограниченной в окрестности точки х 0. Если f (x) – бесконечно большая при § Функция
Рис. 19
Здесь
Бесконечно малые функции Определение и основные теоремы § Функция Например, Теорема 11.1. Алгебраическая сумма бесконечно малых функций есть бесконечно малая функция. Теорема 11.2. Произведение бесконечно малой функции на ограниченную функцию есть БМФ. Следствие 1. Произведение конечного числа БМФ есть БМФ. Следствие 2. Произведение БМФ на число есть БМФ. Теорема 11.3. Частное от деления БМФ на функцию, имеющую предел, отличный от нуля – есть БМФ. Теорема 11 4. Если Теорема 11.5. Доказательство: Пусть Обратно, пусть Основные теоремы о пределах Теорема 11.6. Предел суммы двух функций равен сумме пределов. Доказательство. Пусть Тогда Поскольку сумма двух бесконечно малых функций есть функция бесконечно малая, следовательно
Следствие. Если предел функции существует, то он единственный. Теорема 11.7. Предел произведения двух функций равен произведению пределов, т.е. Теорема 11.8. Теорема 11 9. (Теорема о пределе промежуточной функции.)
Теорема 11.10. Если функция
Техника вычисления пределов. Примеры
Пример 1.
Пример 2.
Пример 3. =
Пример 4.
Пример 5.
Пример 6.
Пример 7. =
Первый замечательный предел Рассмотрим функцию
Так как Разделим данное неравенство на
Следовательно, Итак,
Ниже представлен график функции
Эквивалентные функции § Если Таким образом, поскольку функции
Теорема 11.11. Предел отношения двух бесконечно малых не изменится, если каждую или одну из них заменить эквивалентной ей БМФ. Примеры. 1) 2) § Вообще говоря, если 1. если 2. если существует конечный предел 3. если 4. если Говорят, что БМФ одного порядка стремятся к нулю с одинаковой скоростью. Теорема 11.12 Сумма конечного числа БМФ эквивалентна слагаемому низшего порядка. Пример: при § Слагаемое, эквивалентное сумме бесконечно малых, называется главной частью этой суммы. Замена суммы БМФ ее главной частью называется отбрасыванием БМФ высшего порядка. Теорема 11.13. Разность двух эквивалентных БМФ есть БМФ более высокого порядка. Ниже представлены эквивалентные бесконечно малые, используемые при решении задач на вычисление пределов.
Примеры. 1) 2) 3)
= Второй замечательный предел Вторым замечательным пределом называется предел вида
На графике функции
Данное число является иррациональным, оно названо в честь Леонардо Эйлера, Итак,
Нижеприведенная формула является обобщением второго замечательного предела и используется при вычислениях.
11.7. Техника вычисления пределов вида Пусть
Пример 1. Так как
Пример 2. Так как
Пример 3.
Непрерывность функции
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 933; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.195.219 (0.011 с.) |

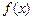 при
при  , если для любого
, если для любого  наществует такое число
наществует такое число 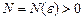 , что при всех
, что при всех  удовлетворяющих неравенству
удовлетворяющих неравенству 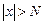 выполняется неравенство
выполняется неравенство 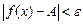 . Записывают:
. Записывают: 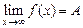 .
.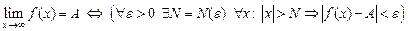
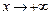 , то пишут
, то пишут 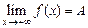 ; если
; если 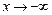 , то
, то 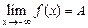 .
. называется бесконечно большой функцией (ББФ) при
называется бесконечно большой функцией (ББФ) при 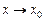 , если
, если . Записывают:
. Записывают:  .
. ; если такая функция принимает только отрицательные значения, то
; если такая функция принимает только отрицательные значения, то  .
.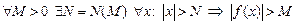 . Записывают:
. Записывают: 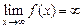 .
. Пример. Рассмотрим функцию
Пример. Рассмотрим функцию  ;
; 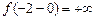 ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 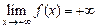 .
.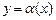 называется бесконечно малой функцией (БМФ) при
называется бесконечно малой функцией (БМФ) при  .
. при
при 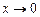 является функцией бесконечно малой, а функция
является функцией бесконечно малой, а функция 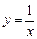 является бесконечно малой функцией при
является бесконечно малой функцией при  – БМФ, то
– БМФ, то 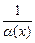 – ББФ. Обратно, если
– ББФ. Обратно, если 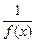 – БМФ.
– БМФ.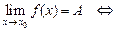 функцию
функцию  . Следовательно, по определению,
. Следовательно, по определению, 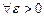
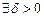 такое, что для всех х из d-окрестности точки х 0 выполняется неравенство
такое, что для всех х из d-окрестности точки х 0 выполняется неравенство 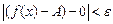 , а это значит, что
, а это значит, что 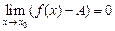 , то есть функция
, то есть функция 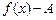 есть БМФ. Обозначив
есть БМФ. Обозначив 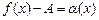 , получаем
, получаем  , что и требовалось доказать.
, что и требовалось доказать.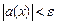 , то есть
, то есть 
 , то
, то 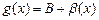 , где
, где  - БМФ.
- БМФ.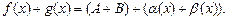
 – бесконечно малая функция. Таким образом, по теореме 5, получим:
– бесконечно малая функция. Таким образом, по теореме 5, получим:



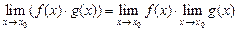 .
. , если
, если  .
. Если функция
Если функция 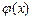 такова, что
такова, что 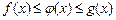 и
и 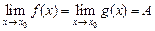 , то
, то 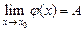 .
. (
( ), то существует
), то существует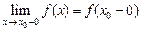 (
( ).
). Для вычисления пределов вида
Для вычисления пределов вида  , где
, где  и
и  многочлены степеней
многочлены степеней 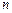 и
и  , необходимо вынести за скобку в числителе
, необходимо вынести за скобку в числителе  и в знаменателе
и в знаменателе  .
.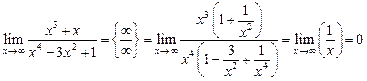 .
. необходимо привести их к пределам вида
необходимо привести их к пределам вида 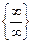 .
.
 . (В данной задаче для преобразования предела к виду
. (В данной задаче для преобразования предела к виду 
 . (В данной задаче для преобразования предела к виду
. (В данной задаче для преобразования предела к виду  необходимо выяснить, определена ли функция при
необходимо выяснить, определена ли функция при 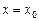 . Если
. Если 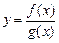 , то
, то  .
.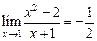 .
. и
и 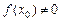 , то
, то 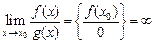 .
.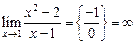 .
.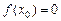 , т.е. если
, т.е. если  , необходимо (в случае
, необходимо (в случае  и
и  ) разделить числитель и знаменатель на
) разделить числитель и знаменатель на 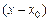 .
.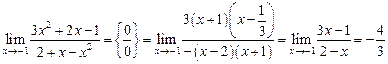 .
.

 .
. . Она не определена при
. Она не определена при  , так как числитель и знаменатель дроби обращаются в нуль. Однако можно заметить, что если
, так как числитель и знаменатель дроби обращаются в нуль. Однако можно заметить, что если  и
и  приблизительно одинаковые. Это можно увидеть на представленном ниже рисунке и сравнить значения в таблице.
приблизительно одинаковые. Это можно увидеть на представленном ниже рисунке и сравнить значения в таблице.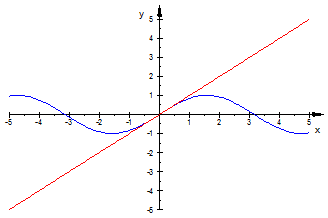
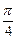

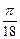

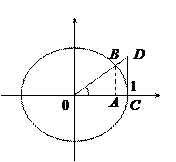 Чем ближе
Чем ближе 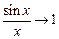 . Итак, докажем формулу
. Итак, докажем формулу 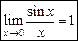 . Для этого рассмотрим единичную окружность. Пусть
. Для этого рассмотрим единичную окружность. Пусть 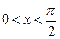 .
.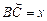 ,
, 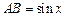 ,
,  .
. , то
, то 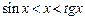 .
. . Знак неравенства при этом не изменится, поскольку
. Знак неравенства при этом не изменится, поскольку  .
. . Воспользуемся теоремой о пределе промежуточной функции. Поскольку при
. Воспользуемся теоремой о пределе промежуточной функции. Поскольку при  и
и  , тогда
, тогда 

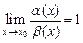 , где
, где  .
. .
.
 . В данном случае заменить невозможно, поскольку функция
. В данном случае заменить невозможно, поскольку функция 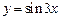 не является бесконечно малой при
не является бесконечно малой при 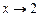 .
.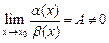 , то
, то  , то
, то  , то
, то  .
.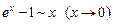
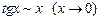





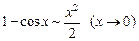

 .
. .
. . Для решения данной задачи сделаем замену переменной. Пусть
. Для решения данной задачи сделаем замену переменной. Пусть  , тогда
, тогда 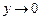 . Имеем:
. Имеем: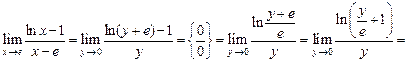
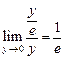 .
. .
.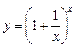 , представленном ниже, видно, что при
, представленном ниже, видно, что при 
 Это число известно читателю как основание натурального логарифма.
Это число известно читателю как основание натурального логарифма.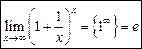 .
.
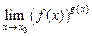 .
. .
. и
и  , то
, то  .
. .
.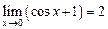 , а
, а 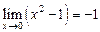 , тогда
, тогда  .
.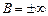 , а
, а  , то
, то

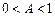


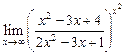 .
.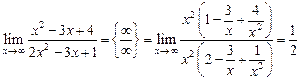 , а
, а 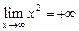 , тогда
, тогда  .
.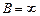 используем формулу
используем формулу
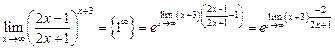 =
=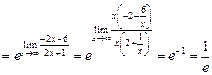 .
.


