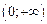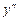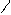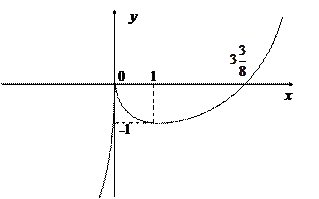Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование поведения функций и построение графиковСодержание книги
Поиск на нашем сайте
ü Возрастание и убывание функций Теорема 15.5. 1) Если функция 2) Если функция непрерывна на отрезке Геометрический смысл этой теоремы в том, что касательные к графику дифференцируемой возрастающей функции образуют острые углы, а убывающей функции – тупые углы с положительным направление оси ü Максимум и минимум функций. § Функция · Функция · Максимумы и минимумы функции называются экстремумами. Теорема 15.6 (необходимое условие существования экстремума). Если дифференцируемая функция · Точки, в которых производная функции
Теорема 15.7 (достаточное условие существования экстремума). Пусть функция
ü Выпуклость и вогнутость кривой. Точки перегиба. § Говорят, что кривая обращена выпуклостью вверх на интервале Теорема 15.8. 1) Если во всех точках интервала 2) Если во всех точках интервала § Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой, называется точкой перегиба кривой. В точке перегиба касательная, если она существует, пересекает кривую, так как с одной стороны от этой точки кривая лежит под касательной, а с другой стороны над нею. Теорема 15.9. Пусть кривая определяется уравнением ü Асимптоты § Прямая l называется асимптотой кривой, если расстояние d от точки Различают два вида асимптот: вертикальные и наклонные. - Прямая - Уравнение наклонной асимптоты - В частности, если Замечание. Асимптоты графика функции
Общее исследование функции и построение ее графика рекомендуется выполнять по следующей схеме: 1. Найти область определения функции. 2. В случае если область определения функции симметрична относительно начала координат, проверить, не является ли функция четной или нечетной, проверить периодичность функции. 3. Найти, если это возможно, точки пересечения графика функции с осями координат. 4. Найти промежутки знакопостоянства функции (промежутки на которых 5. Найти асимптоты графика функции. 6. Найти промежутки монотонности функции, ее экстремумы. 7. Найти промежутки выпуклости и вогнутости графика функции, его точки перегиба. 8. Построить график, используя полученные результаты исследования. Заметим, что приведенная схема исследования не является обязательной. Иногда целесообразно выполнение операций сопровождать постепенным построением графика функции и выбирать дополнительные точки. Пример. Исследовать функцию 1. Данная функция определена при всех 2. 3. Если 4. Интервалы знакопостоянства:
5. Вертикальных асимптот нет, поскольку функция непрерывна на всей области определения. Выясним наличие наклонной асимптоты
6. Найдем промежутки монотонности функции.
Таким образом 7. Найдем промежутки выпуклости и вогнутости графика функции.
8.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.41.80 (0.008 с.) |

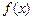 , имеющая производную на отрезке
, имеющая производную на отрезке  , возрастает (убывает) на этом отрезке, то ее производная на отрезке
, возрастает (убывает) на этом отрезке, то ее производная на отрезке 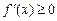 (
( ).
). , причем
, причем 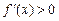 ь (
ь (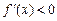 ) для
) для 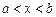 , то эта функция возрастает (убывает) на
, то эта функция возрастает (убывает) на 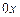 .
.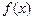 в точке
в точке  имеет максимум, если значение функции
имеет максимум, если значение функции 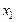 .Иначе говоря, функция
.Иначе говоря, функция  , если
, если 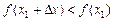 , при любых
, при любых 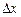 .
. , если
, если  , при любых
, при любых  имеет в точке
имеет в точке 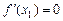 .
. , если все точки кривой лежат выше любой ее касательной на этом интервале. Кривую, обращенную выпуклостью вверх будем называть выпуклой, а обращенную выпуклостью вниз – вогнутой.
, если все точки кривой лежат выше любой ее касательной на этом интервале. Кривую, обращенную выпуклостью вверх будем называть выпуклой, а обращенную выпуклостью вниз – вогнутой.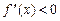 , то кривая
, то кривая 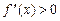 , то кривая
, то кривая 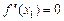 или не существует и при переходе через значение
или не существует и при переходе через значение 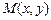 кривой до этой прямой при удалении точки
кривой до этой прямой при удалении точки 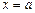 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции 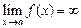 .
. , где
, где  , а
, а 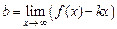 .
. , то
, то 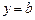 – уравнение горизонтальной асимптоты.
– уравнение горизонтальной асимптоты.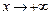 и
и 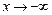 могут быть разными, поэтому при вычислении пределов следует отдельно рассматривать случаи
могут быть разными, поэтому при вычислении пределов следует отдельно рассматривать случаи 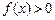 или
или 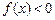 ); выяснить поведение функции на концах промежутка знакопостоянства (в том числе и на бесконечности), построить схематично график на концах промежутка знакопостоянства.
); выяснить поведение функции на концах промежутка знакопостоянства (в том числе и на бесконечности), построить схематично график на концах промежутка знакопостоянства.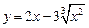 .
. , т.е.
, т.е.  .
. Þ данная функция является функцией общего вида.
Þ данная функция является функцией общего вида.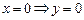 .Таким образом график функции пересекает ось
.Таким образом график функции пересекает ось 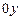 в точке
в точке 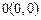 . Если
. Если  . График пересекает ось
. График пересекает ось  и
и  .
.

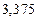
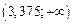

 ,
,  . Таким образом, наклонных асимптот нет.
. Таким образом, наклонных асимптот нет.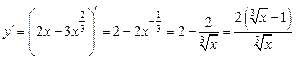 .
.
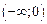
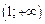

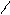


 ,
, 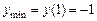 .
.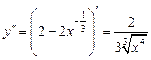 . Вторая производная положительна (кривая вогнута) при всех
. Вторая производная положительна (кривая вогнута) при всех  .
.