
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятия функции и ее графикаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте § Функцией, определенной на множестве X, называют закон f, который каждой точке x Î X ставит в соответствие некоторую единственную точку y Î Y. При этом множество X называют областью определения функции f (обозначают D(f) или D(y)), точку x Î X – аргументом функции, точку y Î Y, соответствующую x, – значением функции в точке x и обозначают y = f (x). Множество Y называют областью значений функции f (обозначают E(y)).
Если элементами X и Y являются действительные числа, то функцию f называют числовой функцией. § Множество точек плоскости с координатами (x, f (x)), x Î X называют графиком функции f. Не для всякой функции график будет линией в обычном представлении, например 9.2. Способы задания функций Для изучения функции ее необходимо задать, т.е. указать правило, позволяющее по значению аргумента функции находить соответствующее ему значение функции. Это правило можно указать различными способами. К таким способам можно отнести аналитический, параметрический, графический, табличный, алгоритмический и описательный. Мы будем, в основном, изучать числовые функции, т.е. функции, у которых область определения и множество значений являются числовыми множествами. Числовые функции чаще всего задаются аналитическим способом, т.е. при помощи формул. Например, Иногда числовые функции на различных числовых промежутках задаются различными формулами. Такова, например, функция
Когда зависимость y от x не задана непосредственно, а вместо этого даны зависимости обоих переменных x и y от некоторого третьего вспомогательного переменного t в виде
то это – параметрический способ задания функции; тогда вспомогательное переменное t называют параметром. При графическом способе задания функции зависимость y от x задают при помощи линии на плоскости x 0 y. Табличный способ задания функции, это способ, когда некоторые значения аргумента и соответствующие им значения функции в определенном порядке размещаются в таблице. Например, тригонометрические функции представлены таблицами Брадиса. В виде таблицы обычно представляют экспериментальные зависимости. Недостаток этого способа состоит в невозможности непосредственного определения значений функции, не входящих в таблицу. Алгоритмический способ задания функции широко используют при вычислениях на ЭВМ. Описательный (или словесный) способ задания функции – это способ, при котором правило соответствия значений функции значениям аргумента выражено словами. Например, функцию, которая каждому числу ставит в соответствие целую часть этого числа Некоторые свойства функций ü Функция ü Функция ü Функцию ü Функцию Обратная функция Пусть задана функция Из определения обратной функции вытекает, что функция Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 882; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |


 определяет лишь одну точку (0,0) на координатной плоскости.
определяет лишь одну точку (0,0) на координатной плоскости. ,
,  ,
,  . Если уравнение, с помощью которого задается функция не разрешено относительно y, то функция называется неявной. Так, известное со школы уравнение окружности с центром в точке
. Если уравнение, с помощью которого задается функция не разрешено относительно y, то функция называется неявной. Так, известное со школы уравнение окружности с центром в точке  не разрешено относительно
не разрешено относительно  и является уравнением неявной функции.
и является уравнением неявной функции.
 , где
, где  ,
, , можно задать следующим образом: «значением функции является наибольшее целое число, не превосходящее х».
, можно задать следующим образом: «значением функции является наибольшее целое число, не превосходящее х». , определяемая на множестве D является четной, если
, определяемая на множестве D является четной, если  выполняются условия
выполняются условия  и
и  ; нечетной, если
; нечетной, если  . График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
. График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат. . Если для любых значений
. Если для любых значений 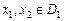 :
:  , то функция называется возрастающей на множестве
, то функция называется возрастающей на множестве  ;
; 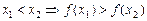 , то функция называется убывающей на множестве
, то функция называется убывающей на множестве  , то функция называется неубывающей на множестве
, то функция называется неубывающей на множестве  , то функция называется невозрастающей на множестве
, то функция называется невозрастающей на множестве 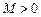 , что для всех
, что для всех  выполняется неравенство
выполняется неравенство 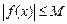 . График ограниченной функции лежит между прямыми
. График ограниченной функции лежит между прямыми  и
и  .
. , что при каждом
, что при каждом  и
и  . Число
. Число  называется периодом функции.
называется периодом функции. соответствует единственное значение
соответствует единственное значение  с областью определения E и множеством значений D. Такая функция
с областью определения E и множеством значений D. Такая функция  и
и  . Тогда всякая строго монотонная функция имеет обратную, при этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).
. Тогда всякая строго монотонная функция имеет обратную, при этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).


