Построение графиков в полярных координатах

 

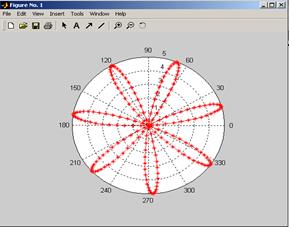
Полярная система координат состоит из заданной фиксированной точки O, называемой полюсом, концентрических окружностей с центром в полюсе и лучей, выходящих из точки O, один из которых OX – полярная ось.

Расположение любой точки M в полярных координатах можно задать положительным числом ρ =|ОМ |, равным расстоянию от полюса до точки, и числом φ,равным величине угла ХОМ (полярный угол); ρ и φ называют полярными координатами точки M, и точку обозначают M (ρ, φ).Для формирования графика в полярных координатах используется функция polar (φ, ρ, s),где φ – массив полярных углов,ρ – массив значений полярных радиусов точек, образующих графики, s – строка, состоящая из трех символов, которые определяют цвет линии, тип маркера и тип линии.

Пусть требуется построить график функции r(φ)=5 cos (2-7φ). При построении в полярных координатах будем изменять аргумент от 0 до 2p(рис. 20).

Необходимо сформировать массивы значений полярного угла φ и полярного радиуса r (аргументом является угол):

 

>> fi=0:0.01:2*pi;

>> r=5*cos(2-7*fi);

>> рolar(fi, r);

 

Можно также указать тип и цвет линий, тогда

 

>>fi=0:pi/200:2*pi;

>> r=5*cos(2-7*fi);

>> рolar(fi, r,'r*-');’

 

 

 

Рис. 20

 

 

Для построения траектории движения точки на плоскости (анимация) предусмотрена функция comet, а для построения
траектории движения точки в трехмерном пространстве – функ-
ция comet3. Это простой способ создать анимированное изображение.

Изобразим движение точки по траектории, заданной параметрически (рис. 21):

>> t=0:0.005:2*pi;

>> x=cos(5*t).*(t+5);

>> y=sin(5*t).*(t+5);

>> comet(x,y)

Рис. 21

Построим траекторию движения точки в пространстве (рис. 22):

>> t=-10*pi:pi/300:10*pi;

>> x=(sin(t).^3).*cos(t);

>> y=(cos(t).^3).*sin(t);

>> comet3(x,y,t)

Рис. 22

Для более сложной анимации можно использовать команды getframe и movieview. Команда getframe захватывает активное окно изображения в один кадр фильма, а команда movieview воспроизводит результат в отдельном окне. Приведенные ниже команды воспроизводят кадры с вибрирующей струной:

>>x=0:0.01:1;

>>for n=0:50

>>plot(x,sin(n*pi/5)*sin(pi*x)),axis([0,1,-2,2])

>>m(n+1)=getframe;

>>end

>>movieview(m)

В приведенном выше примере для организации цикла используется оператор for, работа которого будет описана далее.

Трехмерная графика

 

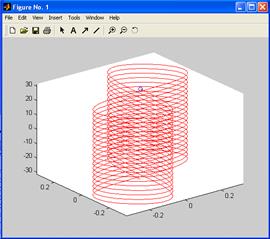
График поверхности (трехмерный график) – это график, положение точки в котором определяется значениями трех координат. Трехмерным аналогом функции plot является функция plot3, которая позволяет создавать трехмерные линии. Если есть три вектора x, y, z, задающих координаты точек в трехмерном пространстве, то при выполнении функции plot3(x,y,z), построится трехмерная линия на плоскости.

Пусть требуется построить график линии, заданной форму-лами

 

x= 2sin(t +p/2),

y= 2cos(t +p/2),

z=t,где t принадлежитдиапазону [0, 8p]

>> t=0:pi/100:8*pi;

>> x=2*sin(t+pi/2);

>> y=2*cos(t+pi/2);

>> z=t;

>> plot3(x,y,z);

>> axis square;

>> grid on

 

Построилась винтовая линия (спираль) (рис. 23).

 

Рис. 23

 

 

Функция plot3, так же как и plot, может иметь дополнительный аргумент, задающий параметры линии (тип линии, цвет и тип маркера). Например, plot3(x,y,z, ‘g*’).

Можно также использовать команду ezplot3:

>> ezplot3('cos(2*pi*t)','sin(2*pi*t)','t',[-2,2])

 

Для вычерчивания каркасных поверхностей в трехмер-
ном пространстве существуют две основные функции: mesh
и surf.

Команда mesh(Z) строит прозрачную сетчатую поверхность, а команда surf(Z) –затененную, где Z – матрица, значения элементов которой определяют соответствующие координаты на графике. Построим прозрачную поверхность для единичной матрицы, задав команды:

 

>>Z=eye(8);

>>mesh(Z)

 

Результат показан на рис. 24.

 

Рис. 24

 

По главной диагонали расположены “пики” – единицы.

Аналогично, задав команду

 

>>surf(Z)

 

получим затененную поверхность (рис. 25).

 

 

Рис. 25

Для построения в трехмерном пространстве функции от двух переменных Z(X, Y) необходимо сначала с помощью векторов x и y задать прямоугольную сетку, которая будет использоваться как основание для построения трехмерной поверхности. Для этого надо воспользоваться функцией meshgrid, которая создает эту сетку из точек в прямоугольной области с заданными интервалами. Диапазоны значений по осям x и y задаются векторами x и y соответственно. Имена векторов и матриц могут различаться.

Пусть значения по осям x и y заданы векторами x и y:

 

>> x=[1 2 3];

>> y=[4 5 6];

 

Сформируем матрицы X и Y с помощью функции meshgrid:

 

>> [X,Y]=meshgrid (x,y)

X =

1 2 3

1 2 3

1 2 3

Y =

4 4 4

5 5 5

6 6 6

 

На основе векторов x и y формируются две матрицы, в которые записываются координаты узлов сетки. Матрица X содержит одинаковые строки, в которых заданы координаты X. Матрица Y содержит одинаковые столбцы, в которых заданы координаты Y. Наложение матриц X и Y позволяет получить пары (x_i и y_j), для которых в дальнейшем вычисляется значение функции Z. Значения функции в узлах сетки записываются в матрицу Z, размерность которой равна размерности матриц X и Y.

Построим график функции, которая имеет вид на заданном интервале х от - 2до2и от y от -4до4с шагом, рав-
ным0,1.

Зададим два вектора x и y, используя запись

>>x =-2: 0.1: 2;

>>y=-4: 0.1:4;

 

Далее вызывается команда

 

>>[X, Y]=meshgrid(x, y);

Значения векторов можно указать прямо внутри команды meshgrid(-2:0.1:2,-4:0.1:4). Если оба вектора одинаковые, то можно записать: [X, Y]= meshgrid(x).

Создаётся прямоугольная сетка с шагом 0,1, которая используется для построения трехмерной поверхности. Каждому значению x ставится в соответствие каждое значение y. Для каждой пары x_i y_j (в узлах сетки) будет вычислено значение функции Z.
В результате сформируется матрица из вычисленных значений функции. После этого можно вызвать команду для вывода изображения на экран.

Ниже приведен пример построения графика с использованием функции plot3 (рис. 26):

 

>>x=-2:0.1:2;

>>y=-4:0.1:4;

>>[X, Y]=meshgrid(x, y);

>>Z=2*X.*exp(-X.^2 - Y.^2);

>>plot3(X, Y, Z)

>>grid

 

 

Рис. 26

 

Более наглядные графики получаются с использованием функции mesh (рис. 27).

 

>> mesh(X,Y,Z)

 

 

Рис. 27

 

Линии на разных участках графика окрашены в разные цвета. Эти цвета соответствуют значениям функции. По умолчанию оттенки красного цвета соответствуют большим значениям функции, а синего – меньшим.

Можно сделать “прозрачной” каркасную поверхность, отобразив ее скрытые части, применив команду hidden off. Отмена – hidden on.

Если использовать функцию meshz(X,Y,Z), то будет видно основание, на котором построен график.

Пример построения сферы. Пусть необходимо начертить
поверхность, которая не может быть представлена выражением z=f(x,y), например сферу x²+y²+z²=1. В этом случае параметры поверхности можно задать, используя подходящую координатную систему, например, сферические координаты. Можно взять в качестве параметров вертикальную координату z и полярную координату q на плоскости x-y.

Если r обозначает расстояние до оси z, то тогда выражение
для сферы становится r ² + z ² = 1, или , отсюда , .

Построение сферической поверхности можно выполнить командами

 

>>[z,t]=meshgrid(-1: 0.1: 1, (0:0.1:2)*pi);

 

Вектор значений Z Вектор значений t от 0 до 2 π

 

>>x=sqrt(1-z.^2).*cos(t);

>>y=sqrt(1-z.^2).*sin(t);

>>surf(x,y,z)

>>axis square

 

Результат приведен на рис. 28.

 

 

Рис. 28

 

Все трехмерные графики, которые мы строили, можно было видеть только из одной точки обзора, т.е. позиции, с которой мы видим трехмерное изображение. В ML можно изменять точку обзора. Эта точка характеризуется двумя параметрами: азимутом (Az) и углом возвышения (El). Азимут определяет угол поворота вокруг оси z и отсчитывается от оси, противоположной y, в направлении против часовой стрелки. Угол возвышения – это угол между отрезком, направленным из начала координат в точку обзора, и плоскостью xy. Точку обзора можно менять программно,
используя функцию view (Az,El) или более просто, используя
специальную кнопку на панели инструментов графического окна Figure – Rotate 3D.

 

Программирование

 

Система ML предоставляет пользователю для решения различных задач мощный язык программирования высокого уровня, понятный непрофессиональным программистам. До сих пор все вычисления и операции мы производили в режиме прямых вычислений. Для эффективной работы с большими наборами команд этого недостаточно. Гораздо лучше было бы записать этот набор команд в виде программы и сохранить ее на диске. Программа представляет собой последовательность команд, записанных
на языкеML(программный код), и сохраняется на диске в виде
m-файла.

Создать m-файл можно с помощью любого текстового редактора, но в ML предусмотрен собственный встроенный редактор EDITOR, который имеет удобные средства для создания и отладки программ.Написанный текст программы студенты должны сохранять в файле на диске, куда разрешена запись, задав ему имя (имя файла и имя каталога не должны содержать русских букв). Этот файл будет иметь расширение. m. Чтобы войти в текстовый редактор, надо выбрать пункт меню File, New, m-file. В редакторе m -файлов можно не только набрать текст программы, но и запустить ее на выполнение. Для сохранения программы на диске надо выбрать пункт меню File, Save as, <имя m-файла>.

m -файлы могут быть двух видов: файл-программа,или Script- файл (S cript m-File), и файл-функция (Function m-File).

Файлы-программы называют Script- файлами, или сценариями. Они состоят из последовательности команд и не имеют входных и выходных параметров. Они обычно используются для автоматизации выполнения большого набора команд. Вызов Script- файла осуществляется просто указанием его имени.

В файлах-функциях описываются функции, определяемые пользователем. Они могут иметь входные и выходные значения. Обращение к файлу-функции осуществляется указанием имени и в круглых скобках списка параметров.

Операторы языка

 

Программа может иметь комментарии. Символ %означает, что далее следует поясняющий текст. Все комментарии начинаются с этого знака. Комментарий не является исполняемым оператором.

Вывод комментариев на экран при выполнении программы обеспечивает оператор echo on. Отменяет вывод комментариев на экран оператор echo off. Оператор pause приостанавливает выполнение программы и ожидает нажатия любой клавиши для продолжения. Оператор pause(n) создает паузу в n секунд.

Операторами языка можно пользоваться как при создании программ, так и в режиме прямых вычислений.

 

Операторы ввода/вывода

 

Интерактивное взаимодействие пользователя с программой реализуется с помощью функций input и display.

Оператор input(<текст>) обеспечивает ввод данных с клавиатуры. Текст, указанный в качестве параметра, заключается в апострофы. Он отображается на экране при вводе. Обращение к этой функции имеет вид

 

< имя переменной >= input(<текст>)

 

Например, при выполнении команды x=input(‘вв. x= ’) на экран выводится текст ’вв. х=’ и ожидается ввод данных с клавиатуры. Введенное данное присваивается переменной х.

При наборе в командном окне

 

>> r=input('Введите радиус ');

 

на экране получим

 

<<Введите радиус>>

 

Далее ожидается ввод значения переменной r.

Если в текст выводимой строки ввести символы ' \ n’, то курсор будет перемещен на следующую строку:

 

>> r=input('Введите \n радиус ');

 

<<Введите

радиус>>

Оператор display(<параметр>) или disp(<параметр>) выводит значение переменной или константы.

disp(A) выведет матрицу А, причем выводятся только значения элементов, а текст ‘А=’, выводиться не будет.

disp(‘Привет’) – на экране будет выведено слово «Привет».