
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение двумерного графика.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте К двумерным графикам относят графики в декартовой и полярной системах координат. Созданный однажды график одного типа нельзя переделать в график другого типа (в отличие от трехмерных графиков). Для построения XY-графика необходимы два ряда данных, откладываемых по осям ОХ и ОУ. Для построения нужно: · щелкнуть мышью в свободном месте рабочего документа; · нажать комбинацию клавиш [shift] + 2 или щелкнуть мышью по палитре графических операторов или выбрать пункт X - Y Plot из меню Insert (Вставка). Появляется пустой график с полями ввода для выражений, отображаемых по осям графика.
XY-график двух векторов. Самый простой и наглядный способ получить декартов график – это сформировать два вектора данных, которые будут отложены вдоль осей ОХ и ОУ. Последовательность построения графика двух векторов х и у показана на рис. 1. В этом случае в шаблоны возле осей вводятся просто имена векторов. Также допускается откладывать по осям элементы векторов, т. е. вводить в шаблоны возле осей имена
Пример 1.
График любой скалярной функции f(х) можно построить двумя способами. Первый заключается в дискретизации значений функции, присвоении этих значений вектору и прорисовке графика вектора.
Пример 2.
Второй способ, называемый быстрым построением графика, заключается во введении функции в один из шаблонов (например, у оси ординат), а имени аргумента – в шаблон у другой оси абсцисс (рис.). В шаблоны слева и справа от аргумента необходимо ввести границы диапазона изменения значений аргумента. Если такой диапазон не задан, по умолчанию график будет построен в диапазоне значений аргумента от -10 до 10.
Пример 3.
Построение графиков в полярных координатах Для создания полярного графика необходимо нажать кнопку Polar Plot на панели Graph (График) и вставить в появившиеся шаблоны имена переменных и функций, которые будут нарисованы в полярной системе координат: угол (нижний шаблон) и радиус-вектор (левый шаблон). Аналогично построению графика в декартовых координатах по осям могут быть отложены два вектора элементы векторов и ранжированные переменные в различных сочетаниях, а также может быть осуществлено быстрое построение графика функции.
Пример 4.
График функции в полярных координатах можно построить также с помощью преобразований полярных координат в декартовые. В примере 5 построен график кардиоиды в полярных координатах, уравнение которого задано в виде
Пример 5.
График может содержать несколько выражений по оси ординат в зависимости от одного выражения по оси абсцисс или несколько значений по оси ординат, согласованных с соответствующими выражениями по оси абсцисс. Чтобы представить графически несколько выражений по оси ординат относительно одного выражения по оси абсцисс, необходимо ввести первое выражение для оси ординат, сопровождаемое запятой. Непосредственно под первым выражением появится пустое поле (шаблон). В появившемся месте ввода записывается имя второй функции, сопровождаемое другой запятой и т.д. Все выражение должно использовать одну и ту же переменную.
Пример 6.
Чтобы построить несколько независимых кривых на одном чертеже, введите два или более выражения, отделяемых запятыми на оси абсцисс, и то же самое число выражений на оси ординат. MathCAD согласует выражения попарно: первое выражение оси абсцисс с первым выражением оси ординат, второе со вторым и т.д. Можно построить до 16 функций на оси ординат в зависимости от одного аргумента на оси абсцисс. Если для каждой кривой используется свой аргумент, то можно отобразить только до 10 графиков.
Все графики на чертеже совместно используют одни границы на осях. Для каждой оси все выражения и границы должны иметь совместимые размерности.
Изменение размеров графика. Чтобы изменить размеры графика, необходимо: 1. Заключить его в выделяющий прямоугольник с помощью щелчка мыши. 2. Переместить указатель мыши к левому нижнему краю выделяющего прямоугольника. Указатель превратится в двойную стрелку. 3. Переместить указатель при нажатой кнопке мыши, растягивая графическую область в желаемом направлении. 4. По достижении желаемого размера отпустить кнопку мыши. Для отмены выделения щелкните мышью вне графической области.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 617; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.009 с.) |

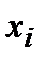 и
и 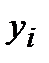 соответственно (рис.). В результате получается график, на котором отложены точки, соответствующие парам элементов векторов, соединенные отрезками прямых линий. Образованная ими ломаная называется рядом данных, или кривой (trace).
соответственно (рис.). В результате получается график, на котором отложены точки, соответствующие парам элементов векторов, соединенные отрезками прямых линий. Образованная ими ломаная называется рядом данных, или кривой (trace).



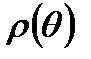 . Уравнения для
. Уравнения для  и
и 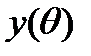 – обычное преобразование полярных координат в прямоугольные (декартовые).
– обычное преобразование полярных координат в прямоугольные (декартовые).





