
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операторы вычисления сумм и произведений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оператор суммирования вычисляет сумму выражений по всем значениям индекса. Оператор произведения работает аналогичным образом. Чтобы создать оператор суммирования в рабочем документе: · щелкните в свободном месте рабочего документа. · Затем нажмите комбинацию [Ctrl]+[Shift]+ 4 или соответствующую кнопку на палитре 3. интегралов и производных.В нижнем поле слева от знака равенства введите имя переменной. Эта переменная - индекс суммирования. Она определена только внутри оператора суммирования, вне оператора может существовать другая переменная с тем же индексом. · В поле справа от знака равенства, а также над знаком суммы введите целое число или любое выражение, принимающее целое значение. · В оставшемся поле введите выражение, которое необходимо просуммировать. Это выражение будет содержать индекс суммирования. Если это выражение имеет несколько членов, используйте скобки (). Для создания оператора произведения нажмите комбинацию клавиш [Ctrl]+[Shift]+3 или щелкните мышью на соответствующей кнопке палитры интегралов (матанализ). Далее применяйте правило, описанное выше. Если индекс суммирования изменяется не с шагом равным единице, то используется обобщенный оператор суммы – обобщенный оператор произведения. 1. Напечатайте i: 1, 1.2; 10 2. Щелкните на свободном месте рабочего документа. Нажмите комбинацию клавиш [Shift]+4 (или [Shift]+3). 3. Щелкните на поле снизу и введите имя дискретного аргумента, который должен быть определен раньше. 4. Щелкните на поле справа от знака суммирования (знака произведения) и внесите выражение, содержащее дискретный аргумент. 5. Нажмите знак равенства, чтобы увидеть результат.
Порядок выполнения работы (включая пример и варианты заданий) Студентам рекомендуется внимательно изучить теоретические сведения, разобрать приведенные там примеры, затем приступить к выполнению поставленного задания. Тестовый пример: 1) Попробуем набрать следующее выражение
и вычислим его значение для a = 0.1, x = 3.5, y = 1. В первую очередь зададим значения переменных, входящих в состав данного выражения. Напечатайте x:3.5 a:0.1 y:1. Затем наберите x-3*a^2. До сих пор правила старшинства позволяли нам просто печатать символы подряд, дальше так продолжать нельзя, так как маркер ввода находится на двойке, и двойка станет числителем, если нажать / Чтобы все выражение стало числителем, нажмите три раза клавишу [space ]. Маркер ввода охватит выражение целиком. Можно поэкспериментировать с другими клавишами курсора, можно щелкать мышью на других частях выражения. Прежде чем перейти к следующему шагу, убедитесь, что маркер ввода охватывает все выражение.
Нажмите / чтобы создать дробную черту напечатайте - 4 + и щелкните на кнопке корня на арифметической палитре. Затем напечатайте y + 1, чтобы завершить знаменатель. Чтобы добавить что-либо снаружи корня нажмите дважды клавишу [ Space ] (пробел). Чтобы вычислить значение данного выражения нажмите клавишу =. 2) 2.1. j:=0..8 2.2. Xj:=j2+1 2.3. наберите j: 0;8 2.4. наберите X [ j: j^2 [Space] +1 2.5. наберите X= Чтобы увидеть все элементы данного вектора, используя полосы прокрутки, щелкните мышью по получившейся таблице вывода. 3) Выполнить вычисления по приведенным ниже формулам. 3.1 Используя переменную типа “дискретный аргумент”, задать элементы вектора.
3.2 Ввести с клавиатуры вектора W, V, матрицы A,B. Вычислить: WxV, W*V, сумму элементов данных векторов, A-1, BT, A*B, A*A-1, (2*A+B)*(A-B2). 3.3 Наберите A: щелкните мышью на палитре матричных операторов. Заполните поля диалогового окна и нажмите клавишу OK. Затем заполните пустые поля матрицы скалярными выражениями. Аналогично задайте матрицу B и вектора W, V.
Контрольные вопросы. 1. Опишите палитры символов. 2. Особенности работы с пакетом инженерных расчетов MathCAD. 3. Как определить переменную в пакете MathCAD? Приведите примеры. 4. Переменная типа “ дискретный аргумент “. Примеры. 5. Как в MathCAD определяется функция? Приведите примеры определения функции. 6. Построение выражения в MathCAD. Цепкие операторы. 7. Редактирование существующего выражения: замена, вставка, удаление оператора; вычисление выражения. 8. Сообщения об ошибках в пакете MathCAD. Исправление ошибок. 9. Допустимые в MathCAD имена переменных и функций. Предопределенные переменные. Числа. 10. Создание вектора (матрицы). Примеры. 11. Векторные и матричные операции (функции). Примеры. 12. Какие операторы используются в Mathcad? Как их можно вводить?
13. Операторы вычисления сумм и произведений: способы задания, примеры. 14. Оператор производной: способ задания, дифференцирование в точке, символьное дифференцирование, примеры. 15. Определенный интеграл: способ задания, переменные пределы интегрирования. Двойной и тройной интегралы. 16. Неопределенный интеграл: способ задания, примеры. 17. Символьный знак равенства, способы его задания, примеры. 18. Встроенные функции. Варианты заданий Вариант 1 1) Вычислить 2) Используя переменную типа «дискретный аргумент», задать 3) Ввести с клавиатуры векторы Вычислить: а) скалярное и векторное произведение векторов W и V; б) сумму элементов данных векторов; в) г) сумму элементов каждой строки матрицы 4) Решить систему уравнений 5) Найти число 6) Вычислить Вариант 2 1) Вычислить 2) Используя переменную типа «дискретный аргумент», задать 3) Ввести с клавиатуры векторы Вычислить: а) скалярное и векторное произведение векторов W и V; б) сумму элементов данных векторов; в) г) сумму элементов каждой строки матрицы 4) Решить систему уравнений 5) Найти число 6) Вычислить Вариант 3 1) Вычислить 2) Используя переменную типа «дискретный аргумент», задать 3) Ввести с клавиатуры векторы Вычислить: а) скалярное и векторное произведение векторов W и V; б) сумму элементов данных векторов; в) г) сумму элементов каждой строки матрицы 4) Решить систему уравнений 5) Найти число 6) Вычислить
Вариант 4 1) Вычислить 2) Используя переменную типа «дискретный аргумент», задать 3) Ввести с клавиатуры векторы Вычислить: а) скалярное и векторное произведение векторов W и V; б) сумму элементов данных векторов; в) г) сумму элементов каждой строки матрицы 4) Решить систему уравнений 5) Найти число 6) Вычислить
Вариант 5 1) Вычислить 2) Используя переменную типа «дискретный аргумент», задать 3) Ввести с клавиатуры векторы Вычислить: а) скалярное и векторное произведение векторов W и V; б) сумму элементов данных векторов; в) г) сумму элементов каждой строки матрицы 4) Решить систему уравнений 5) Найти число 6) Вычислить
Вариант 6 1) Вычислить 2) Используя переменную типа «дискретный аргумент», задать 3) Ввести с клавиатуры векторы Вычислить:
а) скалярное и векторное произведение векторов W и V; б) сумму элементов данных векторов; в) г) сумму элементов каждой строки матрицы 4) Решить систему уравнений 5) Найти число 6) Вычислить
Вариант 7 1) Вычислить 2) Используя переменную типа «дискретный аргумент», задать 3) Ввести с клавиатуры векторы Вычислить: а) скалярное и векторное произведение векторов W и V; б) сумму элементов данных векторов; в) г) сумму элементов каждой строки матрицы 4) Решить систему уравнений 5) Найти число 6) Вычислить
Вариант 8 1) Вычислить 2) Используя переменную типа «дискретный аргумент», задать 3) Ввести с клавиатуры векторы Вычислить: а) скалярное и векторное произведение векторов W и V; б) сумму элементов данных векторов; в) г) сумму элементов каждой строки матрицы 4) Решить систему уравнений 5) Найти число 6) Вычислить Вариант 9. 1) Вычислить 2) Используя переменную типа «дискретный аргумент», задать 3) Ввести с клавиатуры векторы Вычислить: а) скалярное и векторное произведение векторов W и V; б) сумму элементов данных векторов; в) г) сумму элементов каждой строки матрицы 4) Решить систему уравнений 5) Найти число 6) Вычислить Вариант 10 1) Вычислить 2) Используя переменную типа «дискретный аргумент», задать 3) Ввести с клавиатуры векторы Вычислить: а) скалярное и векторное произведение векторов W и V; б) сумму элементов данных векторов; в) г) сумму элементов каждой строки матрицы 4) Решить систему уравнений 5) Найти число 6) Вычислить Тема 2. Графические возможности пакета инженерных расчетов MathCAD. Анимация.
Цель работы: Изучение графических возможностей символьного пакета MathCAD. Приобретение навыков построения графиков функции и поверхностей. Знакомство с возможностями анимации и создания условных выражений. Используемые программные средства: Пакет MathCAD.
Теоретические сведения. В пакете MathCAD встроено несколько различных типов графиков, которые можно разделить на двумерные (или графики на плоскости) и трехмерные (графики в пространстве) В свою очередь двумерные графики делятся на: - XY (декартовый) график (XY Plot); - полярный график (Polar Plot). Среди трехмерных выделяют - график трехмерной поверхности (Surface Plot); - график линий уровня (Contour Plot); - трехмерная гистограмма (3D Bar Plot); - трехмерное множество точек (3D Scatter Plot); - векторное поле (Vector Field Plot). Деление графиков на типы несколько условно, так как управляя установками многочисленных параметров, можно создавать комбинации типов графиков, а также новые типы (например, двумерная гистограмма распределения является разновидностью простого XY-графика). Все графики создаются аналогичным способом, с помощью панели инструментов Graph (График), различия обусловлены отображаемыми данными. Некорректное определение данных приводит, вместо построения графика, к выдаче сообщения об ошибке.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 519; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.91 (0.011 с.) |





 , где
, где  ,
,  ,
,  .
. элементы вектора
элементы вектора 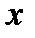 по правилу
по правилу  , если
, если 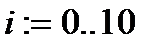 .
. ,
,  ., матрицы
., матрицы  ,
,  .
. ,
,  ,
,  ,
, 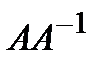 ,
,  ;
; .
. с помощью обратной матрицы и с помощью функции lsolve.
с помощью обратной матрицы и с помощью функции lsolve.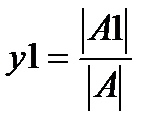 , где
, где  – матрица, полученная из матрицы
– матрица, полученная из матрицы  заменой первого столбца вектором
заменой первого столбца вектором  .
.
 , где
, где  ,
,  ,
,  .
. , если
, если  .
. ,
,  и матрицы
и матрицы  ,
,  .
. с помощью обратной матрицы и с помощью функции lsolve.
с помощью обратной матрицы и с помощью функции lsolve. , где
, где  – матрица, полученная из матрицы
– матрица, полученная из матрицы  .
.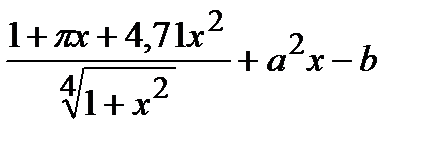 , где
, где  .
.  ,
,  .
. по правилу
по правилу 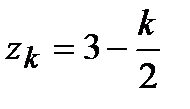 , если
, если  .
. ,
,  и матрицы
и матрицы 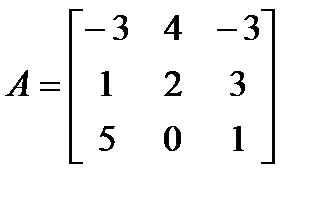 ,
,  .
. , где
, где 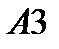 – матрица, полученная из матрицы
– матрица, полученная из матрицы  .
. , где
, где  ,
,  .
.
 .
. ,
,  и матрицы
и матрицы  ,
,  .
. .
.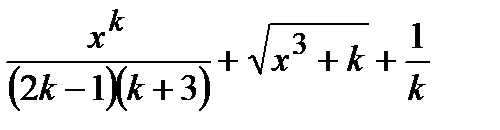 , где
, где 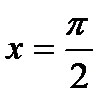 ,
,  .
. , если
, если 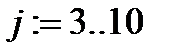 .
. ,
,  и матрицы
и матрицы  ,
,  .
. , где
, где  .
.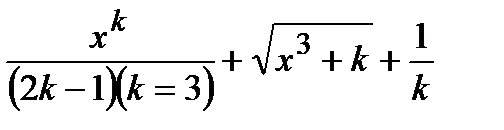 где
где  ,
,  .
. , если
, если  .
.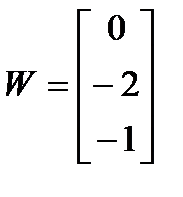 ,
,  и матрицы
и матрицы  ,
, 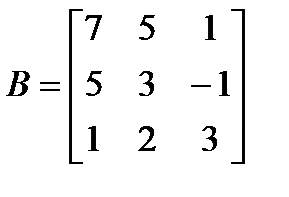 .
. с помощью обратной матрицы и с помощью функции lsolve.
с помощью обратной матрицы и с помощью функции lsolve. , где
, где  .
. , где
, где  ,
,  .
. , если
, если  .
. ,
, 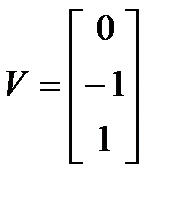 и матрицы
и матрицы 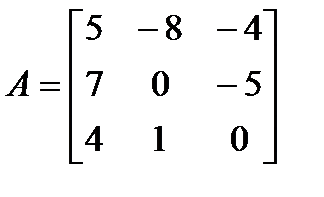 ,
,  .
. .
. , где
, где  ,
,  .
. , если
, если  .
. ,
,  и матрицы
и матрицы  ,
, 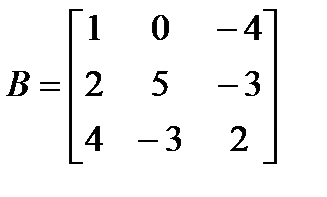 .
. , где
, где  .
. , где
, где  ,
,  .
. , если
, если  .
. ,
,  и матрицы
и матрицы  ,
, 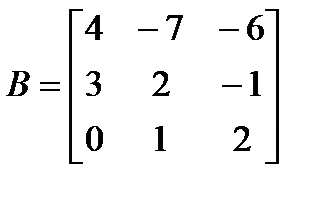 .
.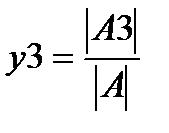 , где
, где  .
.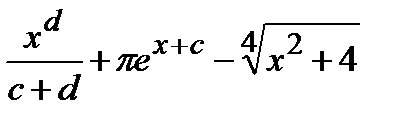 , где
, где  ,
,  ,
,  .
. , если
, если  .
. ,
,  и матрицы
и матрицы  ,
,  .
. с помощью обратной матрицы и с помощью функции lsolve.
с помощью обратной матрицы и с помощью функции lsolve. .
.


