Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точность вычислений, классификация погрешностей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В. Пикулев. Методы компьютерных вычислений Методическое пособие (черновой вариант)
Петрозаводск, 2004
1. Всякий специалист стремится достичь своего уровня некомпетентности. 2. Компьютер – средство многократного увеличения некомпетентности человека. 3. Если две ошибки не принесли результата – испробуй третью. Лоуренс Питер, «Иерархиология». Введение в предмет Численные методы – раздел математики, который со времен Ньютона и Эйлера до настоящего времени находит очень широкое применение в прикладной науке. Традиционно физика является основным источником задач построения математических моделей, описывающих явления окружающего мира, она же является основным потребителем алгоритмов и программ, позволяющих эти задачи с определенным успехом решать. При этом задачей физика является не только правильный выбор программы, которая призвана решать физическую проблему, но и подробный анализ и корректировка используемых алгоритмов, в соответствии с реалиями поставленной задачи и теми математическими правилами, которые либо допускают существование решения с заданной точностью, либо говорят о невозможности такого решения. Примеры современных физических задач, для решения которых используются численные методы – моделирование астрономических событий (рождение и развитие Вселенной), моделирование процессов в микромире (распад и синтез частиц), моделирование установок и процессов термоядерного синтеза. Более «прикладные» задачи – моделирование физических процессов в твердотельных структурах (широко используется в проектировании и изготовлении интегральных схем), моделирование процессов в газах и плазме. Учитывая большую сложность и дороговизну современных экспериментальных методик, и, с другой стороны, постоянный рост производительности вычислительных систем, нетрудно определить тенденцию к увеличению в настоящее время доли модельных (вычислительных) экспериментов. Большое количество численных методов разработано для решения задач математической физики, к которым, например, относятся задачи тепло- и массопереноса, исследования турбулентного движения. К инженерным приложениям численных методов можно отнести расчеты магнитных и электростатических линз для заряженных частиц, различного рода радиотехнические расчеты, включая, например, проектирование СВЧ-волноводов. Любопытно, что как в теоретической физике, так и в инженерной практике решаются численными методами различные задачи теоретической механики, например, задачи столкновения (в том числе динамический хаос). Естественно, такое приложение вычислительной техники к физике, как управление экспериментом и сбор данных, в данном курсе не рассматривается.
План построения вычислительного эксперимента: 1) Создание модели, фиксирующей главные исследуемые факторы. Одновременно формулируются рамки применимости модели. 2) Предварительное исследование математической модели: поверка корректности постановки задачи, существования и единственности решения. 3) Разработка метода расчета сформулированной задачи, построение эффективных вычислительных алгоритмов. 4) Создание программы, осуществляющей моделирование физического объекта, включающей в себя реализации используемых численных методов, проверки корректности ввода исходных и вывода результирующих данных 5) Сравнение полученных результатов моделирования с тестовыми примерами и экспериментальными данными; решение вопроса о правильности практического моделирования (иначе повторяются пункты 3 и 4). 6) Решение вопроса о достоверности предложенной математической модели. Если модель не описывает экспериментальные данные, возврат на пункт 1. Таким образом, численный эксперимент – это не однократное вычисление по некоторому набору формул, а многостадийный процесс программирования, анализа результатов и их погрешностей. Задача (Класс может представлять собой координатное бесконечномерное пространство, множество непрерывных функций и др.) Численный алгоритм – однозначная последовательность действий, которые могут привести к одному решению. Отсутствие устойчивости обычно означает, что сравнительно небольшой погрешности δ x соответствует весьма большое δ y, а значит получаемое решение будет далеко от истинного. К такой задаче численные методы применять бессмысленно, ибо погрешности численного расчета будут катастрофически нарастать. Устойчивость задачи определяется (1) математической формулировкой, (2) используемым алгоритмом расчета. Пример неустойчивой задачи в первом случае:
Система Система Пример алгоритмической неустойчивости – вычисление производных численными методами: какой бы метод мы не использовали, приходится вычитать весьма мало различающиеся числа. В настоящее время развиты методы решения многих некорректных задач, которые основаны на решении вспомогательной корректной задачи, близкой к исходной. Если выполняется условие для норм (модулей)
Численное интегрирование. Задача численного интегрирования состоит в замене исходной подинтегральной функции f(x), для которой трудно или невозможно записать первообразную в аналитике, некоторой аппроксимирующей функцией φ(x). Такой функцией обычно является полином (кусочный полином)
где а r(x) – априорная погрешность метода на отдельном шаге интегрирования.
Обзор методов интегрирования. Методы вычисления однократных интегралов называются квадратурными (для кратных интегралов – кубатурными). 1) Методы Ньютона-Котеса. Здесь φ(x) – полином различных степеней. Сюда относятся метод прямоугольников, трапеций, Симпсона. 2) Методы статистических испытаний (методы Монте-Карло). Здесь узлы сетки для квадратурного или кубатурного интегрирования выбираются с помощью датчика случайных чисел, ответ носит вероятностный характер. В основном применяются для вычисления кратных интегралов. 3) Сплайновые методы. Здесь φ(x) – кусочный полином с условиями связи между отдельными полиномами посредством системы коэффициентов. 4) Методы наивысшей алгебраической точности. Обеспечивают оптимальную расстановку узлов сетки интегрирования и выбор весовых коэффициентов ρ(x) в задаче Метод прямоугольников. Различают метод левых, правых и средних прямоугольников. Суть метода ясна из рисунка. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени – отрезком, параллельным оси абсцисс.
Выведем формулу метода прямоугольников из анализа разложения функции f(x) в ряд Тейлора вблизи некоторой точки x = x i.
Рассмотрим диапазон интегрирования от x i до x i + h, где h – шаг интегрирования. Вычислим =
В случае равного шага h на всем диапазоне интегрирования общая формула имеет вид
Здесь n – число разбиений интервала интегрирования,
Метод средних прямоугольников. Здесь на каждом интервале значение функции считается в точке
Метод трапеций. Аппроксимация в этом методе осуществляется полиномом первой степени. Суть метода ясна из рисунка. На единичном интервале В случае равномерной сетки (h = const)
При этом
Методы Монте-Карло. 1)
2) двумерная случайная величина – оценка площадей. Рассматриваются две равномерно распределенных случайных величины x i и y i, которые можно рассматривать как координаты точки в двумерном пространстве. За приближенное значение интеграла принимается количества точек S, попавших под кривую y = f (x), к общему числу испытаний N, т.е. И первый, и второй случай легко обобщаются на кратные интегралы.
Вторая формула Рунге. Так как модуль и знак апостериорной погрешности из формулы (4) известны, можно уточнить искомое значение Алгоритм Эйткена. Способ оценки погрешности для случая, когда порядок метода p неизвестен. Более того, алгоритм позволяет опытным путем определить и порядок метода. Для этого в третий раз вычислим значение величины w с шагом k 2 h:
Приравняем правые части выражений (5) и (3):
Алгоритм метода Гаусса 1) Прямой ход. Идея метода состоит в последовательном исключении неизвестных из системы n линейных уравнений. На примере первого уравнения системы (2) рассмотрим выражение для x 1:
Подставим выражение для x 1 во второе и все остальные уравнения системы:
Для расширенной матрицы коэффициентов это означает, что каждый элемент первой строки следует поделить на диагональный элемент, а все остальные строки преобразовать, как показано выше. Таким образом, станут равны нулю все коэффициенты первого столбца, лежащие ниже главной диагонали. Затем аналогичная процедура проводится со второй строкой матрицы и нижележащими строками, при этом первая строка и первый столбец уже не изменяются. И так далее до тех пор, пока все коэффициенты, лежащие ниже главной диагонали, не будут равны нулю. Общие формулы прямого хода:
k = 1… n, j = 1… n +1. Звездочкой отмечены элементы k -й строки с измененными значениями, которые будут подставлены в следующую формулу. Для определенности будем считать первый индекс – по строкам, второй – по столбцам.
i = k +1… n, j = 1… n +1, k фиксировано в уравнении (3). Для уменьшения количества действий достаточно изменять значения элементов, находящихся выше главной диагонали.
2) Обратный ход. Второй этап решения СЛАУ методом Гаусса называется обратным ходом и состоит в последовательном определении x k, начиная с x n, так как для последнего решение фактически получено. Общая формула:
Таким образом, вычисление корней
3) Выбор главного элемента. Для уменьшения погрешности вычислений следует стремиться к тому, чтобы на главной диагонали матрицы стояли максимальные по модулю значения коэффициентов. Алгоритмически этого можно добиться, переставляя строки таким образом, чтобы на диагонали стоял наибольший по модулю элемент текущего столбца. Такая процедура называется выбором главного элемента и осуществляется всякий раз при переходе к новой строке в прямом цикле метода Гаусса.
4) Погрешность метода. Расчет невязок. Точность результатов будет определяться только точностью выполнения арифметических операций при преобразовании элементов матрицы, т.е. ошибкой округления. Контроль правильности полученного решения осуществляется подстановкой полученных значений x 1… x n в исходную систему уравнений и вычислением невязок, т.е. разностей между правыми и левыми частями уравнений:
Специально отметим, что подставлять найденные значения
5) Преимущества и недостатки метода. Преимущество метода в том, что он позволяет достичь результата за заранее известное и фиксированное число действий. Точность результатов будет определяться правильным выбором порядка коэффициентов в матрице
Блок-схема алгоритма метода Гаусса без выбора главного элемента.
Интерполяция функций. Многомерная интерполяция.
Метод дихотомии (бисекций).
Итерации продолжаются, пока длина отрезка не станет меньше 2ξ – заданной точности. Тогда середина последнего отрезка даст значение корня с требуемой точностью. В качестве иного критерия можно взять | f (x)| ≤ ξy. Скорость сходимости метода невелика, однако он прост и надежен. Метод неприменим к корням четной кратности. Если на отрезке несколько корней, то заранее неизвестно, к какому из них сойдется процесс. Если на заданном интервале предполагается несколько корней, то существует возможность последовательно исключать найденные корни из рассмотрения. Для этого воспользуемся вспомогательной функцией Метод хорд. Идея метода проиллюстрирована рисунком. Задается интервал [ x 0, x 1], на котором f (x 0) f (x 1) ≤ 0, между точками x 0 и x 1 строится хорда, стягивающая f (x). Очередное приближение берется в точке x 2, где хорда пересекает ось абсцисс. В качестве нового интервала для продолжения итерационного процесса выбирается тот, на концах которого функция имеет разные знаки. Условия выхода из итерационного цикла:
Для вывода итерационной формулы процесса найдем точку пересечения хорды (описываемой уравнением прямой) с осью абсцисс: ax 2 + b = 0, где Отсюда легко выразить Метод хорд в большинстве случаев работает быстрее, чем метод дихотомии. Недостатки метода те же, что и в предыдущем случае.
Метод секущих. В отличие от метода Ньютона, можно заменить производную первой разделенной разностью, найденной по двум последним итерациям, т.е. заменить касательную секущей. При этом первый шаг итерационного процесса запишется так:
Для начала итерационного процесса необходимо задать x 0и x 1, которые не обязательно ограничивают интервал, на котором функция должна менять знак; это могут быть любые две точки на кривой. Выход из итерационного процесса по условию
Метод простых итераций. Суть метода простых итераций в принципе совпадает с методом, изложенным для решения систем линейных алгебраических уравнений. Для нелинейного уравнения метод основан на переходе от уравнения f (x) = 0 (2) к эквивалентному уравнению x = φ (x). Этот переход можно осуществить разными способами, в зависимости от вида f (x). Например, можно положить φ (x) = x + bf (x), (3) где b = const, при этом корни исходного уравнения (2) не изменятся. Если известно начальное приближение к корню x 0, то новое приближение x 1 = φ (x 0), т.е. общая схема итерационного процесса: x k+1 = φ (x k). (4) Наиболее простой критерий окончания процесса Критерий сходимости метода простых итераций: если вблизи корня | φ /(x)| < 1, то итерации сходятся. Если указанное условие справедливо для любого x, то итерации сходятся при любом начальном приближении. Исследуем выбор константы b в функции (3) с точки зрения обеспечения максимальной скорости сходимости. В соответствии с критерием сходимости наибольшая скорость сходимости обеспечивается при | φ /(x)| = 0. При этом, исходя из (3), b = –1/ f /(x), и итерационная формула (4) переходит в
т.е. в формулу метода Ньютона (1). Таким образом, метод Ньютона является частным случаем метода простых итераций, обеспечивающим самую высокую скорость сходимости из всех возможных вариантов выбора функции φ (x).
Постановка задачи. Требуется решить систему нелинейных уравнений Убедиться в существовании решения и количестве корней, а также выбрать нулевое приближение в случае системы двух уравнений с двумя неизвестными можно, построив графики функций в удобных координатах. В случае сложных функций можно посмотреть поведение аппроксимирующих их полиномов. Для трех и более неизвестных, а также для комплексных корней, удовлетворительных способов подбора начального приближения нет. Метод Ньютона. Обозначим
Это можно интерпретировать как первые два члена разложения функции в ряд Тейлора вблизи
Мы получили систему линейных уравнений, неизвестными в которой выступают величины
где в данном случае
Критерием окончания итерационного процесса является условие Блок-схема метода Ньютона для решения систем нелинейных уравнений.
Так как метод Ньютона отличается высокой скоростью сходимости при выполнении условий сходимости, на практике критерием работоспособности метода является число итераций: если оно оказывается большим (для большинства задач >100), то начальное приближение выбрано плохо.
Частным случаем решения (4) методом Ньютона системы из двух нелинейных уравнений
являются следующие легко программируемые формулы итерационного процесса:
Метод простых итераций. Метод простых итераций для решения (1) аналогичен методу, рассмотренному при решении нелинейных уравнений с одним неизвестным. Прежде всего, выбирается начальное приближение
и по ней осуществляется итерационный цикл. Если итерации сходятся, то они сходятся к решению уравнения (1). Обозначим Например, для исходной системы уравнений
где множители
Метод спуска. Рассмотрим функцию Поиск минимума функций. Задачи поиска максимума эквивалентны задачам поиска минимума, так как требуется лишь поменять знак перед функцией. Для поиска минимума необходимо определить интервал, на котором функция могла бы иметь минимум. Для этого можно использовать (1) графическое представление функции, (2) аналитический анализ аппроксимирующей функции и (3) сведения о математической модели исследуемого процесса (т.е. законы поведения данной функции).
Определения. Функция f (x) имеет локальный минимум при некотором Точка, в которой функция достигает наименьшего на множестве X значения, называется абсолютным минимумом функции. Для нахождения абсолютного минимума требуется найти все локальные минимумы и выбрать наименьшее значение. Задачу называют детерминированной, если погрешностью вычисления (или экспериментального определения) функции f (x) можно пренебречь. В противном случае задачу называют стохастической. Все изложенные далее методы применимы только к детерминированным задачам. Метод дробления.
| x k+1 – x k| ≤ ξ. (1) Данный метод является одним из самых медленных для поиска минимума. Основное достоинство данного алгоритма – возможность использования в программах управления экспериментальными исследованиями, когда значения функции f(x) последовательно измеряются с шагом h ≥ h min. Метод золотого сечения. Пусть f (x) задана и кусочно-непрерывна на [ xL, xR ], и имеет на этом отрезке только один локальный минимум. Золотое сечение, о котором упоминал ещё Евклид, состоит в разбиении интервала [ xL, xR ] точкой x 1 на две части таким образом, что отношение длины всего отрезка к его большей части равно отношению большей части к меньшей:
Таким образом, возьмем на отрезке две точки x 1и x 2, симметрично относительно границ делящие исходный отрезок в отношении золотого сечения:
где коэффициент Если f (x 1) < f (x 2), мы должны сузить отрезок справа, т.е. новое значение x R = x 2, в противном случае x L = x 1. Оставшаяся внутри нового отрезка точка является первым приближением к минимуму и делит этот отрезок в отношении золотого сечения. Таким образом, на каждой итерации приближения к минимуму (см. рисунок) нам нужно ставить только одну точку (x 1 или x 2), в которой считать значение функции и сравнивать его с предыдущим. Условием выхода из итерационного процесса будет, подобно предыдущему случаю, условие | x 2 – x 1| ≤ ξ. Метод отличается высокой скоростью сходимости, обычно изысканной компактностью программной реализации и всегда находит точку, минимальную на заданном интервале. Метод парабол. Пусть f (x) имеет первую и вторую производную. Разложим f (x) в ряд Тейлора в некоторой точке x k, ограничиваясь при этом тремя членами разложения:
Обычно в практических реализациях данного метода не используют аналитический вид первой и второй производных f (x). Их заменяют конечно-разностными аппроксимациями. Наиболее часто берут симметричные разности с постоянным шагом h:
Это эквивалентно аппроксимации функции параболой, проходящей через три близкие точки x k+ h, x k, x k– h. Окончательное выражение, по которому можно строить итерационный процесс, таково:
Данный метод отличается от вышеизложенных высокой скоростью сходимости. Вблизи экстремума, вплоть до расстояний ~ h 2, сходимость практически не отличается от квадратичной. Однако алгоритм требует постоянного контроля сходимости. Например, итерационный процесс будет сходиться к минимуму, если 1) знаменатель формулы (4) должен быть >0. Если это не так, нужно сделать шаг в обратном направлении, причем достаточно большой. Обычно в итерационном процессе полагают 2)
Метод координатного спуска.
  | |||||||||
|
| Поделиться: |

 называется корректно поставленной, если для любых входных данных х из некоторого класса решение y существует, единственно и устойчиво по входным данным.
называется корректно поставленной, если для любых входных данных х из некоторого класса решение y существует, единственно и устойчиво по входным данным. имеет решение
имеет решение  , однако
, однако имеет решение
имеет решение  , то есть разница в коэффициенте менее 1% приводит к изменению решения в 300%.
, то есть разница в коэффициенте менее 1% приводит к изменению решения в 300%. , то задача устойчива. Однако если константа С очень велика, то фактически наблюдается слабая устойчивость. Такую задачу называют плохо обусловленной. Пример – дифференциальное уравнение
, то задача устойчива. Однако если константа С очень велика, то фактически наблюдается слабая устойчивость. Такую задачу называют плохо обусловленной. Пример – дифференциальное уравнение  с начальными условиями
с начальными условиями  . Общее решение дифференциального уравнения есть
. Общее решение дифференциального уравнения есть  . Начальные условия приводят к обнулению первого слагаемого, но если из-за погрешности начальных данных это будет не так, то при возрастании x влияние первого слагаемого будет катастрофически нарастать.
. Начальные условия приводят к обнулению первого слагаемого, но если из-за погрешности начальных данных это будет не так, то при возрастании x влияние первого слагаемого будет катастрофически нарастать. . То есть:
. То есть: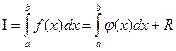 ,
, – априорная погрешность метода на интервале интегрирования,
– априорная погрешность метода на интервале интегрирования,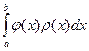 . Сюда относится метод Гаусса-Кристоффеля (вычисление несобственных интегралов) и метод Маркова.
. Сюда относится метод Гаусса-Кристоффеля (вычисление несобственных интегралов) и метод Маркова.
 …
… …=
…= =
=  . Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности.
. Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности.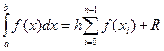 .
. . Для справедливости существования этой оценки необходимо существование непрерывной f’ (x).
. Для справедливости существования этой оценки необходимо существование непрерывной f’ (x). , то есть
, то есть 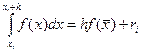 . Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше:
. Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше:
 .
. .
.
 , а
, а  . Погрешность метода трапеций в два раза выше, чем у метода средних прямоугольников! Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда. В силу разных знаков погрешности в формулах трапеций и средних прямоугольников истинное значение интеграла обычно лежит между двумя этими оценками.
. Погрешность метода трапеций в два раза выше, чем у метода средних прямоугольников! Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда. В силу разных знаков погрешности в формулах трапеций и средних прямоугольников истинное значение интеграла обычно лежит между двумя этими оценками. одномерная случайная величина – статистический вариант метода прямоугольников.
одномерная случайная величина – статистический вариант метода прямоугольников. В качестве текущего узла xi берется случайное число, равномерно распределенное на интервале интегрирования [ a, b ]. Проведя N вычислений, значение интеграла определим по следующей формуле:
В качестве текущего узла xi берется случайное число, равномерно распределенное на интервале интегрирования [ a, b ]. Проведя N вычислений, значение интеграла определим по следующей формуле:  . Для R можно утверждать хотя бы ~
. Для R можно утверждать хотя бы ~ 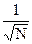 .
. .
. . Это вторая формула Рунге. Однако теперь погрешность w corr не определена, известно лишь, что она по модулю меньше R 0.
. Это вторая формула Рунге. Однако теперь погрешность w corr не определена, известно лишь, что она по модулю меньше R 0. . (5)
. (5) . Отсюда:
. Отсюда: . Подставим сюда значение R 0 из (4):
. Подставим сюда значение R 0 из (4):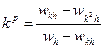 . Из этой формулы определяем знаменатель для (4). Кроме того, определяем порядок
. Из этой формулы определяем знаменатель для (4). Кроме того, определяем порядок  . Для правильно реализованных алгоритмов методов априорных и апостериорных порядки должны получиться совпадающими. Программная реализация формул Рунге позволяет вычислить определенные интегралы с заданной точностью, когда выбор необходимого числа разбиений интервала интегрирования осуществляется автоматически. Пример – уже рассмотренная ранее формула Ромберга.
. Для правильно реализованных алгоритмов методов априорных и апостериорных порядки должны получиться совпадающими. Программная реализация формул Рунге позволяет вычислить определенные интегралы с заданной точностью, когда выбор необходимого числа разбиений интервала интегрирования осуществляется автоматически. Пример – уже рассмотренная ранее формула Ромберга. .
. .
. , (3)
, (3) , (4)
, (4) . (5)
. (5) происходит за 2/3 n 3 арифметических действий.
происходит за 2/3 n 3 арифметических действий. , где k = 1… n. (6)
, где k = 1… n. (6) и ее размерностью. Недостатком метода является резкое увеличение времени и погрешности вычислений с ростом n.
и ее размерностью. Недостатком метода является резкое увеличение времени и погрешности вычислений с ростом n.
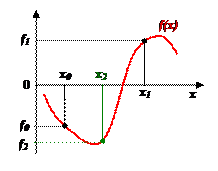 Иначе называется методом половинного деления. Пусть задан начальный интервал [ x 0, x 1], на котором f (x 0) f (x 1) ≤ 0 (т.е. внутри имеется не менее чем один корень). Найдем x 2 = ½ (x 0 + x 1) и вычислим f (x 2). Если f (x 0) f (x 2) ≤ 0, используем для дальнейшего деления отрезок [ x 0, x 2], если > 0 – используем для дальнейшего деления отрезок [ x 1, x 2], и продолжаем деление пополам.
Иначе называется методом половинного деления. Пусть задан начальный интервал [ x 0, x 1], на котором f (x 0) f (x 1) ≤ 0 (т.е. внутри имеется не менее чем один корень). Найдем x 2 = ½ (x 0 + x 1) и вычислим f (x 2). Если f (x 0) f (x 2) ≤ 0, используем для дальнейшего деления отрезок [ x 0, x 2], если > 0 – используем для дальнейшего деления отрезок [ x 1, x 2], и продолжаем деление пополам. , где
, где  – только что найденный корень. Для функций f (x) и g (x) совпадают все корни, за исключением
– только что найденный корень. Для функций f (x) и g (x) совпадают все корни, за исключением  или
или | f (x)| ≤ ξ y.
| f (x)| ≤ ξ y. ; b = f (x 0) – ax 0.
; b = f (x 0) – ax 0. .
. .
.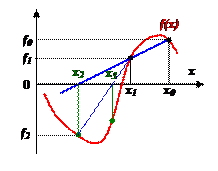 Сходимость может быть немонотонной даже вблизи корня. При этом вблизи корня может происходить потеря точности, т.н. «разболтка решения», особенно значительная в случае кратных корней. От разболтки страхуются приемом Гарвика: выбирают некоторое ξ x и ведут итерации до выполнения условия
Сходимость может быть немонотонной даже вблизи корня. При этом вблизи корня может происходить потеря точности, т.н. «разболтка решения», особенно значительная в случае кратных корней. От разболтки страхуются приемом Гарвика: выбирают некоторое ξ x и ведут итерации до выполнения условия  . Затем продолжают расчет, пока
. Затем продолжают расчет, пока  убывает. Первое же возрастание может свидетельствовать о начале разболтки, а значит, расчет следует прекратить, а последнюю итерацию не использовать.
убывает. Первое же возрастание может свидетельствовать о начале разболтки, а значит, расчет следует прекратить, а последнюю итерацию не использовать. .
. ,
, (1). В координатном виде эту задачу можно записать так:
(1). В координатном виде эту задачу можно записать так:  , где 1 ≤ k ≤ n.
, где 1 ≤ k ≤ n.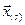 некоторое приближение к корню системы уравнений
некоторое приближение к корню системы уравнений  . Пусть малое
. Пусть малое  . Вблизи
. Вблизи  , 1 ≤ k ≤ n. (2)
, 1 ≤ k ≤ n. (2) . В соответствии с (1), приравнивая (2) к нулю, получим:
. В соответствии с (1), приравнивая (2) к нулю, получим: , 1 ≤ k ≤ n. (3)
, 1 ≤ k ≤ n. (3) . Решив ее, например, методом Гаусса, мы получим некое новое приближение к
. Решив ее, например, методом Гаусса, мы получим некое новое приближение к  . Выражение (3) можно представить как обобщение на систему уравнений итерационного метода Ньютона, рассмотренного в предыдущей главе:
. Выражение (3) можно представить как обобщение на систему уравнений итерационного метода Ньютона, рассмотренного в предыдущей главе: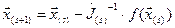 , (4)
, (4)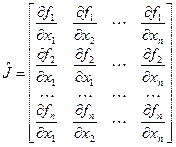 – матрица Якоби, которая считается для каждого (s) приближения.
– матрица Якоби, которая считается для каждого (s) приближения. (Можем принять под
(Можем принять под  как норму
как норму  , так и
, так и  ). Достоинством метода является высокая скорость сходимости. Сходимость метода зависит от выбора начального приближения: если
). Достоинством метода является высокая скорость сходимости. Сходимость метода зависит от выбора начального приближения: если  , то итерации сходятся к корню. Недостатком метода является вычислительная сложность: на каждой итерации требуется находить матрицу частных производных и решать систему линейных уравнений. Кроме того, если аналитический вид частных производных неизвестен, их надо считать численными методами.
, то итерации сходятся к корню. Недостатком метода является вычислительная сложность: на каждой итерации требуется находить матрицу частных производных и решать систему линейных уравнений. Кроме того, если аналитический вид частных производных неизвестен, их надо считать численными методами.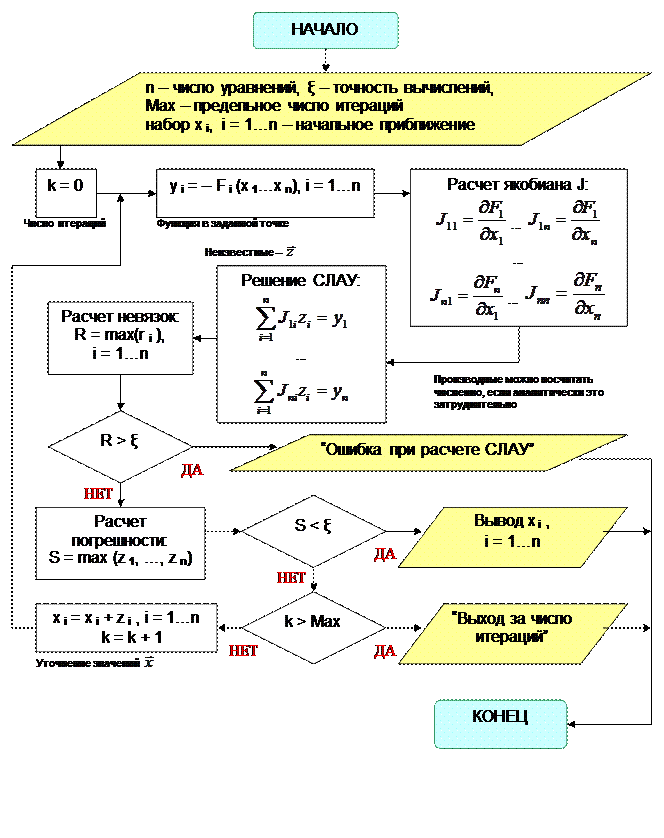

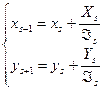 , где
, где  ,
, ,
, 
 , а исходная система уравнений преобразуется к эквивалентной системе вида
, а исходная система уравнений преобразуется к эквивалентной системе вида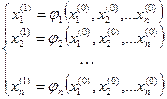 , (5)
, (5) . Достаточным условием сходимости является
. Достаточным условием сходимости является 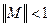 . Скорость сходимости метода сильно зависит от вида конкретно подбираемых функций
. Скорость сходимости метода сильно зависит от вида конкретно подбираемых функций  , которые должны одновременно удовлетворять условиям эквивалентности (5) и (1), и обеспечивать сходимость итерационного процесса.
, которые должны одновременно удовлетворять условиям эквивалентности (5) и (1), и обеспечивать сходимость итерационного процесса. эквивалентная итерационная система (5) может быть представлена в следующем виде:
эквивалентная итерационная система (5) может быть представлена в следующем виде: ,
, = –0.15и
= –0.15и  = –0.1 подбираются из анализа условий сходимости.
= –0.1 подбираются из анализа условий сходимости. . Она неотрицательна и обращается в нуль в том и только в том случае, если
. Она неотрицательна и обращается в нуль в том и только в том случае, если  , то полученные значения
, то полученные значения  ,
,  . Требуется, чтобы на множестве X функция f (x) была по крайней мере кусочно-непрерывной.
. Требуется, чтобы на множестве X функция f (x) была по крайней мере кусочно-непрерывной. Наиболее простой метод поиска минимума. Пусть дана начальная точка x 0, а также величина и знак шага h, определяющие движение из этой точки в сторону предполагаемого минимума f (x). Метод заключается в последовательном дроблении исходного шага h с изменением его знака при выполнении условия f (x k+1) > f (x k), где k – порядковый номер вычисляемой точки. Например, как только очередное значение функции стало больше предыдущего, выполняется h = – h /3 и процесс продолжается до тех пор, пока
Наиболее простой метод поиска минимума. Пусть дана начальная точка x 0, а также величина и знак шага h, определяющие движение из этой точки в сторону предполагаемого минимума f (x). Метод заключается в последовательном дроблении исходного шага h с изменением его знака при выполнении условия f (x k+1) > f (x k), где k – порядковый номер вычисляемой точки. Например, как только очередное значение функции стало больше предыдущего, выполняется h = – h /3 и процесс продолжается до тех пор, пока . (2)
. (2)
 ,
, ,
,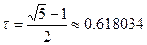 .
. . (3)
. (3) Иными словами, аппроксимируем нашу функцию в точке x k параболой. Для этой параболы можно аналитически вычислить положение экстремума как корень уравнения первой производной от (3):
Иными словами, аппроксимируем нашу функцию в точке x k параболой. Для этой параболы можно аналитически вычислить положение экстремума как корень уравнения первой производной от (3): 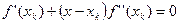 . Пусть минимум аппроксимирующей параболы находится в точке x k+1. Тогда вычислив значение функции f (x k+1), мы получаем новую точку приближения к минимуму.
. Пусть минимум аппроксимирующей параболы находится в точке x k+1. Тогда вычислив значение функции f (x k+1), мы получаем новую точку приближения к минимуму. ;
;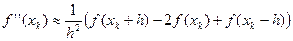 .
. . (4)
. (4) . Иногда ради упрощения расчетов полагают
. Иногда ради упрощения расчетов полагают  , однако это существенно уменьшает скорость сходимости.
, однако это существенно уменьшает скорость сходимости.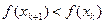 . Если это не так, то от x k следует сделать шаг
. Если это не так, то от x k следует сделать шаг  с τ = ½. Если и при этом условие убывания не выполнено, уменьшают τ и вновь делают шаг.
с τ = ½. Если и при этом условие убывания не выполнено, уменьшают τ и вновь делают шаг.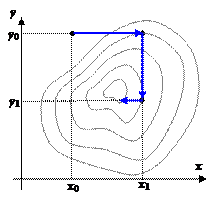 Пусть требуется найти минимум f (x, y). Выберем нулевое приближение (x 0, y 0). Рассмотрим функцию одной переменной f (x, y 0) и найдем ее минимум, используя любой из рассмотренных выше способов. Пусть этот минимум оказался в точке (x 1, y 0). Теперь точно так же будем искать минимум функции одной переменной f (x 1, y). Этот минимум окажется в точке (x 1, y 1). Одна итерация спусков завершена. Будем повторять циклы, постепенно приближаясь ко дну котловины, пока не выполнится условие
Пусть требуется найти минимум f (x, y). Выберем нулевое приближение (x 0, y 0). Рассмотрим функцию одной переменной f (x, y 0) и найдем ее минимум, используя любой из рассмотренных выше способов. Пусть этот минимум оказался в точке (x 1, y 0). Теперь точно так же будем искать минимум функции одной переменной f (x 1, y). Этот минимум окажется в точке (x 1, y 1). Одна итерация спусков завершена. Будем повторять циклы, постепенно приближаясь ко дну котловины, пока не выполнится условие  .
.