
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аппроксимация ортогональными классическими полиномами.Содержание книги
Поиск на нашем сайте
Представленные ниже полиномы, относящиеся ко многочленам Якоби, обладают свойством ортогональности в изложенном выше смысле. То есть, для достижения высокой точности вычислений рекомендуется выбирать базисные функции для аппроксимации в виде этих полиномов. 1) Полиномы Чебышева. Определены и ортогональны на [–1, 1] с весом Строятся следующим образом (рекуррентная формула): T 0(x) = 1; T 1(x) = x; T k+1(x) = 2 xT k(x) – T k–1(x).
2) Полиномы Лежандра. Определены и ортогональны на [–1, 1] с весом Строятся следующим образом (рекуррентная формула): L 0(x) = 1; L 1(x) = x;
Сглаживание и линейная регрессия. Рассмотрим несколько наиболее простых с точки зрения программной реализации случаев аппроксимации (сглаживания). 1) Линейная регрессия. В случае линейного варианта МНК (линейная регрессия) φ (x) = a + bx можно сразу получить значения коэффициентов a и b по следующим формулам:
где 2) Линейное сглаживание по трём точкам.
3) Линейное сглаживание по пяти точкам.
Решение нелинейных уравнений с одним неизвестным. Общие сведения о численном решении уравнений с одним неизвестным. Пусть задана непрерывная функция f (x). Требуется найти корни уравнения f (x) = 0 численными методами – это и является постановкой задачи. Численное решение уравнения распадается на несколько подзадач: 1) Анализ количества, характера и расположения корней (обычно путем построения графика функции или исходя из физического смысла исследуемой модели). Здесь возможны следующие варианты:
2) Локализация корней (разбиение на интервалы) и выбор начального приближения к каждому корню. В простейшем случае можно протабулировать функцию с заданным шагом. Если в двух соседних узлах функция будет иметь разные знаки, то между этими узлами лежит нечетное число корней уравнения (по меньшей мере один). 3) Вычисление каждого (или интересующего нас) корня уравнения с требуемой точностью. Уточнение происходит с помощью методов, изложенных ниже.
Метод дихотомии (бисекций).
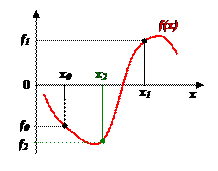
Итерации продолжаются, пока длина отрезка не станет меньше 2ξ – заданной точности. Тогда середина последнего отрезка даст значение корня с требуемой точностью. В качестве иного критерия можно взять | f (x)| ≤ ξy. Скорость сходимости метода невелика, однако он прост и надежен. Метод неприменим к корням четной кратности. Если на отрезке несколько корней, то заранее неизвестно, к какому из них сойдется процесс. Если на заданном интервале предполагается несколько корней, то существует возможность последовательно исключать найденные корни из рассмотрения. Для этого воспользуемся вспомогательной функцией Метод хорд. Идея метода проиллюстрирована рисунком. Задается интервал [ x 0, x 1], на котором f (x 0) f (x 1) ≤ 0, между точками x 0 и x 1 строится хорда, стягивающая f (x). Очередное приближение берется в точке x 2, где хорда пересекает ось абсцисс. В качестве нового интервала для продолжения итерационного процесса выбирается тот, на концах которого функция имеет разные знаки. Условия выхода из итерационного цикла:
Для вывода итерационной формулы процесса найдем точку пересечения хорды (описываемой уравнением прямой) с осью абсцисс: ax 2 + b = 0, где Отсюда легко выразить Метод хорд в большинстве случаев работает быстрее, чем метод дихотомии. Недостатки метода те же, что и в предыдущем случае.
|
|||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.113.14 (0.008 с.) |

 . В интервал ортогональности всегда можно вписать область определения исходной функции с помощью линейных преобразований.
. В интервал ортогональности всегда можно вписать область определения исходной функции с помощью линейных преобразований.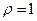 .
. .
. ,
, ,
, ,
,  .
. Иначе называется методом половинного деления. Пусть задан начальный интервал [ x 0, x 1], на котором f (x 0) f (x 1) ≤ 0 (т.е. внутри имеется не менее чем один корень). Найдем x 2 = ½ (x 0 + x 1) и вычислим f (x 2). Если f (x 0) f (x 2) ≤ 0, используем для дальнейшего деления отрезок [ x 0, x 2], если > 0 – используем для дальнейшего деления отрезок [ x 1, x 2], и продолжаем деление пополам.
Иначе называется методом половинного деления. Пусть задан начальный интервал [ x 0, x 1], на котором f (x 0) f (x 1) ≤ 0 (т.е. внутри имеется не менее чем один корень). Найдем x 2 = ½ (x 0 + x 1) и вычислим f (x 2). Если f (x 0) f (x 2) ≤ 0, используем для дальнейшего деления отрезок [ x 0, x 2], если > 0 – используем для дальнейшего деления отрезок [ x 1, x 2], и продолжаем деление пополам. , где
, где  – только что найденный корень. Для функций f (x) и g (x) совпадают все корни, за исключением
– только что найденный корень. Для функций f (x) и g (x) совпадают все корни, за исключением  или
или | f (x)| ≤ ξ y.
| f (x)| ≤ ξ y. ; b = f (x 0) – ax 0.
; b = f (x 0) – ax 0. .
.


