Численные методы поиска минимума функции нескольких переменных.

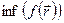Будем рассматривать методы поиска минимума в многомерных задачах на примере функции двух переменных f (x, y), так как эти методы легко аппроксимировать на случай трех и более измерений. Все эффективные методы поиска минимума сводятся к построению траекторий, вдоль которых функция убывает. Разные методы отличаются способами построения таких траекторий, так как метод, приспособленный к одному типу рельефа, может оказаться плохим для рельефа другого типа. Различают следующие типы рельефа:

1) Котловинный (гладкая функция)

2) Истинный овраг

3) Разрешимый овраг

4) Неупорядоченный

 

Метод координатного спуска.

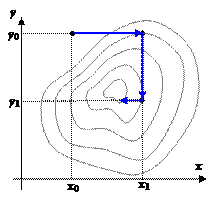Пусть требуется найти минимум f (x, y). Выберем нулевое приближение (x ₀, y ₀). Рассмотрим функцию одной переменной f (x, y ₀) и найдем ее минимум, используя любой из рассмотренных выше способов. Пусть этот минимум оказался в точке (x ₁, y ₀). Теперь точно так же будем искать минимум функции одной переменной f (x ₁, y). Этот минимум окажется в точке (x ₁, y ₁). Одна итерация спусков завершена. Будем повторять циклы, постепенно приближаясь ко дну котловины, пока не выполнится условие .

x

?

y

Сходимость метода зависит от вида функции и выбора нулевого приближения. Вблизи невырожденного минимума гладкой функции спуск по координатам линейно сходится к минимуму. Если линии уровня образуют истинный овраг, возможен случай, когда спуск по одной координате приводит на дно оврага, а любое движение по следующей координате ведет на подъем. Процесс координатного спуска в данном случае не сходится к минимуму.

При попадании траектории спуска в разрешимый овраг сходимость становится чрезвычайно медленной. В физических задачах овражный рельеф указывает на то, что не учтена какая-то закономерность, определяющая связь между переменными. Явный учет этой закономерности облегчает использование численных методов.

Метод градиентного (наискорейшего) спуска.

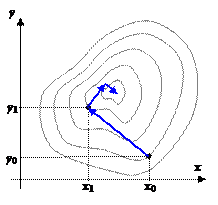В этом методе функция минимизируется по направлению, в котором она быстрее всего убывает, т.е. в направлении, обратном . Вдоль этого направления функция зависит от одной параметрической переменной t, для нахождения минимума которой можно воспользоваться любым известным методом поиска минимума функции одной переменной. Спуск из точки начального приближения против градиента до минимума t определяет новую точку 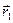, в которой вновь определяется градиент и делается следующий спуск. Условием окончания процесса, как и в случае координатного спуска, будет .

С помощью метода градиентного спуска минимум гладких функций в общем случае находится быстрее, чем при использовании координатного спуска, однако нахождение градиента численными методами может свести на нет полученный выигрыш. Сходимость плохая для функций с овражным рельефом, т.е. с точки зрения сходимости градиентный спуск не лучше спуска по координатам.

Каждый спуск заканчивается в точке, где линия градиента касательна к линии (поверхности) уровня. Это означает, что каждый следующий спуск должен быть перпендикулярен предыдущему. Таким образом, вместо поиска градиента в каждой новой точке можно сосчитать градиент в начальной точке, и развернуть оси координат так, чтобы одна их осей была параллельна градиенту, а затем осуществлять спуск координатным методом.

Метод оврагов.

Ставится задача найти минимум 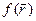для овражной функции. Для этого выбираются две близкие точк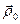и и 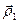, и осуществляется спуск из этих точек (любым методом), причем высокой точности сходимости не требуется. Конечные точки спуска 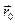и будут лежать вблизи дна оврага. Затем осуществляется движение вдоль прямой, соединяющей и в сторону уменьшения (как бы вблизи дна оврага). Движение может быть осуществлено только на один шаг ~ h, направление выбирается из сравнения значения функции в точках и . Таким образом, находится новая точка . Так как возможно, что точка уже лежит на склоне оврага, а не на дне, то из нее снова осуществляется спуск в новую точку . Затем намечается новый путь по дну оврага вдоль прямой, соединяющей и . 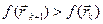Если – процесс прекращается, а в качестве минимума в данном овраге используется значение .

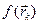Метод оврагов рассчитан на то, чтобы пройти вдоль оврага и выйти в котловину около минимума. В этой котловине значения минимума лучше уточнять другими методами.