Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцирование сложной функции.Содержание книги Поиск на нашем сайте
Дифференцирование сложной функции. Рассмотрим функцию y = sin x2. Пусть y = f (g (x)) - сложная функция, причем функция u = g (x) дифференцируема в точке x, а функция y = f (u) дифференцируема в соответствующей точке u. причем y
2.Таблица основных производных
3. Нахождение промежутков возрастания, убывания, точки экстремума Определение возрастающей функции. Функция y=f(x) возрастает на интервале X, если для любых Определение убывающей функции. Функция y=f(x) убывает на интервале X, если для любых
Точку
Точку Под окрестностью точки Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.
Вот формулировки признаков возрастания и убывания функции на интервале: · если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X; · если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X. Коллинеарные вектора Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 2).
Сонаправленные вектора Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b Противоположно направленные вектора Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b (рис. 4).
Компланарные вектора Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).
Всегда возможно найти плоскости параллельную двум произвольным векторам, по-этому любые два вектора всегда компланарные.
Равные вектора Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины: a = b, если a↑↑b и |a| = |b|.
Единичный вектор Определение. Единичным вектором или ортом - называется вектор, длина которого равна единице.
8. Нахождение суммы, разности, произведение векторов Умножение вектора на число Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».
Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены. Обозначения: коллинеарность векторов записывают привычным значком параллельности: Произведением ненулевого вектора Правило умножения вектора на число легче понять с помощью рисунка:
9.Коллинеарные и компланарные векторы Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.\ Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны.Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Все выше упомянутые случаи легко рассмотреть, если разместить векторы на рёбрах параллелепипеда. 1. Любые два вектора находятся в одной плоскости, но в одной плоскости можно разместить и векторы AA1−→−, CC1−→− и AD−→−, то есть эти векторы компланарны. Также компланарны векторы AA1−→−, AB−→− и CC1−→−, так как два из этих векторов параллельны. Легко представить, что если привести их к общему началу, то вектор CC1−→− совпадет с вектором AA1−→−. 2. Например, векторы AB−→−, AD−→− и AA1−→− не компланарны, так как их нельзя разместить в одной и той же плоскости. Признак компланарности трёх векторов: Пусть векторы a⃗ и b⃗ не коллинеарны. Если для вектора c⃗ существует единственная пара реальных чисел x и y, такая, чтоc⃗ =x⋅a⃗ +y⋅b⃗, то векторы a⃗, b⃗ и c⃗ компланарны. Справедливо и обратное утверждение: Если три вектора a⃗, b⃗ и c⃗ компланарны и векторы a⃗ и b⃗ не коллинеарны, то вектор c⃗ можно разложить по векторам a⃗ и b⃗ одним единственным образом. 10. Координаты точки, координаты вектора Если даны две точки плоскости Если даны две точки пространства То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора. Обязательно нужно понимать различие между координатами точек и координатами векторов: Координаты точек – это обычные координаты в прямоугольной системе координат. Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя. Координаты же вектора – это его разложение по базису Записи координат точек и координат векторов вроде бы схожи:
11.Координаты суммы и разности векторов, произведение на число Сложение векторов (сумма векторов) a + b есть операция вычисления вектора c, все элементы которого равны попарной сумме соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен: сi = ai + bi Вычитание векторов (разность векторов) a - b есть операция вычисления вектора c, все элементы которого равны попарной разности соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен: сi = ai - bi В случае пространственной задачи сумму и разность векторов a = {ax; ay; az} и b = {bx; by; bz} можно найти воспользовавшись следующими формулами: a + b = {ax + bx; ay + by; az + bz} a - b = {ax - bx; ay - by; az - bz} Пример 3. Найти сумму векторов a = {1; 2; 5} и b = {4; 8; 1}. Решение: a + b = {1 + 4; 2 + 8; 5 + 1} = {5; 10; 6} Пример 4. Найти разность векторов a = {1; 2; 5} и b = {4; 8; 1}. Решение: a - b = {1 - 4; 2 - 8; 5 - 1} = {-3; -6; 4} Определение. Середина отрезка - это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек.
В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии,... Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка. Формула вычисления координат середины отрезка с концами A(xa, ya, za) и B(xb, yb, zb) в пространстве:
13.Вычисление длины вектора по его координатам Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB. Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Длина вектора |a| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координа Угол между векторами Угол между двумя векторами
Если угол между двумя векторами острый, то их скалярное произведение положительно; если угол между векторами тупой, то скалярное произведение этих векторов отрицательно. Скалярное произведение двух ненулевых векторов равно нулю, тогда и только тогда, когда эти векторы ортогональны. Задание. Найти угол между векторами Решение. Косинус искомого угла
16. Вычисление угла между прямыми, прямой и плоскостью
Угол между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, - это угол между прямой и ее проекцией на эту плоскость.
Определение угла между прямой и плоскостью позволяет заключить, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми: самой прямой и ее проекцией на плоскость. Следовательно, угол между прямой и плоскостью есть острый угол.
Угол между перпендикулярными прямой и плоскостью считают равным § 69. Вычисление угла между прямыми. Задача вычисления угла между двумя прямыми в пространстве решается так же, как и на плоскости (§ 32). Обозначим через φ величину угла между прямыми l 1и l 2, а через ψ — величину угла между направляющими векторами а и b этих прямых.
Тогда, если ψ <90° (рис. 206, а), то φ = ψ; если же ψ > 90° (рис. 206,6), то φ = 180° — ψ. Очевидно, что в обоих случаях верно равенство cos φ = |cos ψ|. По формуле (1) § 20 имеем
следовательно, Пусть прямые заданы своими каноническими уравнениями
Тогда угол φ между прямыми определяется с помощью формулы
Если одна из прямых (или обе) задана не каноничecкими уравнениями, то для вычисления угла нужно найти координаты направляющих векторов этих прямых, а затем воспользоваться формулой (1). 17. Параллельные прямые, Теоремы о параллельных прямых
Определение. Две прямые на плоскости называются параллельными, если они не имеют общих точек.
Две прямые в трехмерном пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.
Замечания.
Выводы. Случаи взаимного расположения прямой и плоскости: а) прямая лежит в плоскости;
19.Скрещивающиеся прямые. Теоремы о скрещивающихся прямых
Признак скрещивающихся прямых. Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).
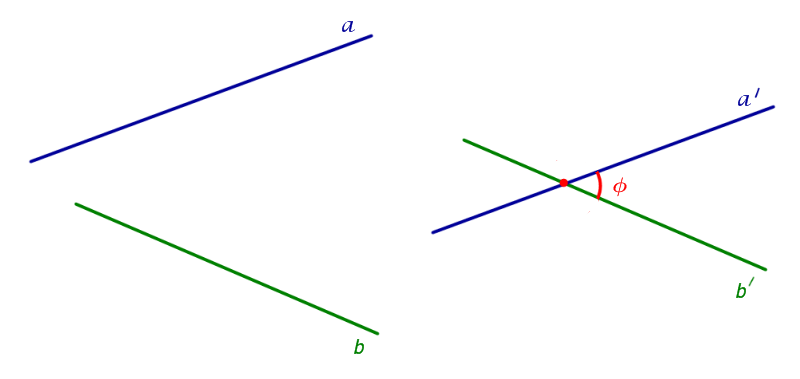
Углом между скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым (рис. 2).
Рис.2 На рисунке 2 изображены скрещивающиеся прямые a и b. Прямая a' параллельна прямой a, прямая b' параллельна прямой b. Прямые a' и b' пересекаются. Угол φ и является углом между скрещивающимися прямыми a и b.
20. Параллельность плоскостей Две плоскости параллельны, если они не имеют общих точек. Это определение. Однако в практических целях чаще используется признак параллельности плоскостей: Плоскости параллельны друг другу, если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.
Свойства параллельных плоскостей: 1. Если две плоскости параллельны третьей, то они параллельны друг другу. 2. Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны. 3. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
21.Перпендикулярные прямые Две прямые называются перпендикулярными, если они пересекаются под прямым углом. Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Пусть b – данная прямая, а точка A принадлежит этой прямой. Возьмем некоторый луч b1 на прямой b с начальной точкой в A. Отложим от луча b1 угол (a1b1), равный 90°. По определению прямая содержащая луч a1 будет перпендикулярная прямой b. 22. Перпендикулярность прямой и плоскости Признак перпендикулярности прямой и плоскости
23.Расстояние от точки до прямой. Теорема о трёх перпендикулярах АН – расстояние от точки до плоскости. 24. Угол между прямой и плоскостью
25. Двугранный угол
26. Перпендикулярность плоскостей
27. Многогранники. Определение, грани, вершины,ребра. Выпуклые многогранники
28. Прямоугольный параллелепипед:.опр. свойства, площадь поверхности, объём
Параллелепипед является четырехугольной призмой.
29. Призма. Прямая призма, правильная призма, площадь поверхности и объём
30.Пирамида. Правильная пирамида, площадь поверхности и объём
31. Правильные многогранники. Типы правильных многогранников.
32. Цилиндр. Площадь поверхности и объём.
33.Конус. Усеченный конус. Площадь поверхности и объём.
34. Сфера и шар. Уравнение сферы
35.Взаимное расположение сферы и плоскости
36. Площадь поверхности сферы и объём шара.
37. Шаровой сегмент, шаровой слой, шаровой сектор
Дифференцирование сложной функции. Рассмотрим функцию y = sin x2. Пусть y = f (g (x)) - сложная функция, причем функция u = g (x) дифференцируема в точке x, а функция y = f (u) дифференцируема в соответствующей точке u. причем y
2.Таблица основных производных
|

 = f
= f  g
g  = n
= n  xn −1
xn −1
 x
x
 x
x
 a
a  0
0  =1
=1
 lna
lna
 и
и  выполняется неравенство
выполняется неравенство  . Другими словами – большему значению аргумента соответствует большее значение функции.
. Другими словами – большему значению аргумента соответствует большее значение функции. . Другими словами – большему значению аргумента соответствует меньшее значение функции.
. Другими словами – большему значению аргумента соответствует меньшее значение функции.

 называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство
называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство  . Значение функции в точке максимума называют максимумом функции и обозначают
. Значение функции в точке максимума называют максимумом функции и обозначают  .
. . Значение функции в точке минимума называют минимумом функции и обозначают
. Значение функции в точке минимума называют минимумом функции и обозначают  .
. , где
, где  - достаточно малое положительное число.
- достаточно малое положительное число.

 рис. 4
рис. 4


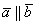 , при этом возможна детализация:
, при этом возможна детализация: 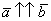 (векторы сонаправлены) или
(векторы сонаправлены) или  (векторы направлены противоположно).
(векторы направлены противоположно). на число
на число  является такой вектор
является такой вектор  , длина которого равна
, длина которого равна  , причём векторы
, причём векторы  и противоположно направлены при
и противоположно направлены при  .
.

 и
и  , то вектор
, то вектор  имеет следующие координаты:
имеет следующие координаты:
 и
и  , то вектор
, то вектор 
 , в данном случае
, в данном случае  . Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости
. Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости  , а смысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства
, а смысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства
 ,
,  :
:
 и
и 



 , а угол между параллельными прямой и плоскостью либо не определяют вовсе, либо считают равным
, а угол между параллельными прямой и плоскостью либо не определяют вовсе, либо считают равным  .
.



 (1)
(1)

 рис. 22
рис. 22