Признаки параллельности двух прямых. Свойства параллельных прямых

Признаки параллельности двух прямых

Теорема 1.Если при пересечении двух прямых секущей:

1. накрест лежащие углы равны, или

2. соответственные углы равны, или

3. сумма односторонних углов равна 180°, то прямые параллельны (рис.1).

 

18.Параллельность прямой и плоскости

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек (а || )

Признак параллельности прямой и плоскости.

Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.

рис. 21

Замечания.

рис. 22

1. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. 2. Если одна из двух параллельных прямых параллельна данной плоскости, а другая прямая имеет с плоскостью общую точку, то эта прямая лежит в данной плоскости.

Выводы.

Случаи взаимного расположения прямой и плоскости:

а) прямая лежит в плоскости;
б) прямая и плоскость имеют только одну общую точку;
в) прямая и плоскость не имеют ни одной общей точки.

 

 

19.Скрещивающиеся прямые. Теоремы о скрещивающихся прямых

скрещивающиеся прямые

Две прямые называют скрещивающимися прямыми, если не существует плоскости, содержащей обе прямые.

Признак скрещивающихся прямых. Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).

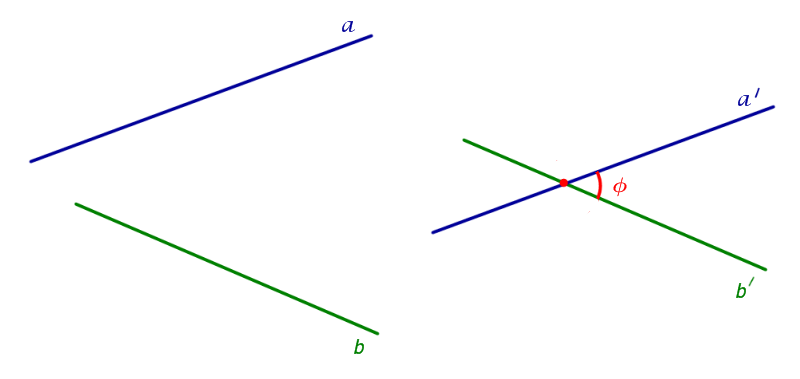
Углом между скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым (рис. 2).

Рис.2

На рисунке 2 изображены скрещивающиеся прямые a и b. Прямая a' параллельна прямой a, прямая b' параллельна прямой b. Прямые a' и b' пересекаются. Угол φ и является углом между скрещивающимися прямыми a и b.

 

 

20. Параллельность плоскостей

Две плоскости параллельны, если они не имеют общих точек.

Это определение. Однако в практических целях чаще используется признак параллельности плоскостей:

Плоскости параллельны друг другу, если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.

Свойства параллельных плоскостей:

1. Если две плоскости параллельны третьей, то они параллельны друг другу.

2. Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.

3. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

 

21.Перпендикулярные прямые

Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Прямая a пересекается с прямой b под прямым углом в точке A. Можно зависать используя значок перпендикулярности: a ⊥ b. Это читается так: прямая а перпендикулярна прямой b.
Следует заметить, что смежный угол и вертикальный угол с прямым углом тоже прямые.

Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну.

Доказательство.

Пусть b – данная прямая, а точка A принадлежит этой прямой. Возьмем некоторый луч b1 на прямой b с начальной точкой в A. Отложим от луча b1 угол (a1b1), равный 90°. По определению прямая содержащая луч a1 будет перпендикулярная прямой b.
Допустим, существует другая прямая перпендикулярная прямой b и проходящая через точку A. Возьмем на этой прямой луч с1, исходящий из точки A и лежащий в той же полуплоскости, что и луч a1. Тогда ∠ (a1b1) = ∠ (c1b1) = 90 º. Но согласно аксиоме 8, в данную полуплоскость можно отложить только один угол, равный 90 º. Следовательно, нельзя провести другую прямую перпендикулярную прямой b через точку A в заданную полуплоскость. Теорема доказана.

Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, имеющий одним из концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра. AB – перпендикуляр к прямой a. Точка A – основание перпендикуляра.

22. Перпендикулярность прямой и плоскости

Признак перпендикулярности прямой и плоскости

 

23.Расстояние от точки до прямой. Теорема о трёх перпендикулярах

АН – расстояние от точки до плоскости.

24. Угол между прямой и плоскостью

 

 

25. Двугранный угол

 

 

26. Перпендикулярность плоскостей

 

27. Многогранники. Определение, грани, вершины,ребра. Выпуклые многогранники

 

 

28. Прямоугольный параллелепипед:.опр. свойства, площадь поверхности, объём

 

Параллелепипед является четырехугольной призмой.

 

29. Призма. Прямая призма, правильная призма, площадь поверхности и объём

 

30.Пирамида. Правильная пирамида, площадь поверхности и объём

 

31. Правильные многогранники. Типы правильных многогранников.

 

32. Цилиндр. Площадь поверхности и объём.

 

 

33.Конус. Усеченный конус. Площадь поверхности и объём.

 

 

 

34. Сфера и шар. Уравнение сферы

 

35.Взаимное расположение сферы и плоскости

 

36. Площадь поверхности сферы и объём шара.

 

37. Шаровой сегмент, шаровой слой, шаровой сектор