
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая интерпретация.Содержание книги Поиск на нашем сайте
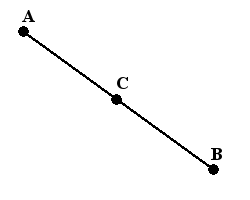
Произведение ненулевого вектора на число - это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа. Алгебраическая интерпретация. Произведение ненулевого вектора на число - это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число. В случае пространственной задачи произведение вектора a = {ax; ay; az} и числа k можно найти воспользовавшись следующей формулой: k · a = {k · ax; k · ay; k · az} 12 Координаты середины отрезка Координаты середины отрезка равны полусуммам координат его концов: если концы отрезка – A (x 1; y 1) и B (x 2; y 2), то координаты его середины – Определение. Середина отрезка - это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек.
В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии,... Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка. Формула вычисления координат середины отрезка с концами A(xa, ya, za) и B(xb, yb, zb) в пространстве:
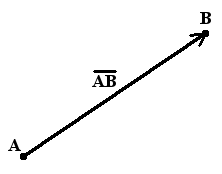
13.Вычисление длины вектора по его координатам Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB. Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Длина вектора |a| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координа Формула длины вектора для плоских задач В случае плоской задачи модуль вектора a = {ax; ay} можно найти воспользовавшись следующей формулой: |a| = √ax2 + ay2
Формула длины вектора для пространственных задач В случае пространственной задачи модуль вектора a = {ax; ay; az} можно найти воспользовавшись следующей формулой: |a| = √ax2 + ay2 + az2 14.Скалярное произведение векторов
Скалярным произведением двух ненулевых векторов
Задание. Вычислить скалярное произведение векторов Решение. Так как из условия Если хотя бы один из векторов
Свойства скалярного произведения: 1° 2° 3° Если 4° Если 5° 6°
Если векторы
15.Вычисление угла между векторами
Угол между векторами Угол между двумя векторами
Если угол между двумя векторами острый, то их скалярное произведение положительно; если угол между векторами тупой, то скалярное произведение этих векторов отрицательно. Скалярное произведение двух ненулевых векторов равно нулю, тогда и только тогда, когда эти векторы ортогональны. Задание. Найти угол между векторами Решение. Косинус искомого угла
16. Вычисление угла между прямыми, прямой и плоскостью
Угол между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, - это угол между прямой и ее проекцией на эту плоскость. Определение угла между прямой и плоскостью позволяет заключить, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми: самой прямой и ее проекцией на плоскость. Следовательно, угол между прямой и плоскостью есть острый угол.
Угол между перпендикулярными прямой и плоскостью считают равным § 69. Вычисление угла между прямыми. Задача вычисления угла между двумя прямыми в пространстве решается так же, как и на плоскости (§ 32). Обозначим через φ величину угла между прямыми l 1и l 2, а через ψ — величину угла между направляющими векторами а и b этих прямых.
Тогда, если ψ <90° (рис. 206, а), то φ = ψ; если же ψ > 90° (рис. 206,6), то φ = 180° — ψ. Очевидно, что в обоих случаях верно равенство cos φ = |cos ψ|. По формуле (1) § 20 имеем
следовательно, Пусть прямые заданы своими каноническими уравнениями
Тогда угол φ между прямыми определяется с помощью формулы
Если одна из прямых (или обе) задана не каноничecкими уравнениями, то для вычисления угла нужно найти координаты направляющих векторов этих прямых, а затем воспользоваться формулой (1). 17. Параллельные прямые, Теоремы о параллельных прямых
Определение. Две прямые на плоскости называются параллельными, если они не имеют общих точек.
Две прямые в трехмерном пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 817; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.148.65 (0.009 с.) |


 и
и  называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними: 
 ,
,  , а
, а  , то
, то 
 .
. - симметричность.
- симметричность. . Обозначается
. Обозначается  и называется скалярный квадрат.
и называется скалярный квадрат. , то
, то 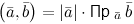
 и
и  . Верно и обратное утверждение.
. Верно и обратное утверждение.

 ,
,  , то их скалярное произведение вычисляется по формуле:
, то их скалярное произведение вычисляется по формуле:

 и
и 



 , а угол между параллельными прямой и плоскостью либо не определяют вовсе, либо считают равным
, а угол между параллельными прямой и плоскостью либо не определяют вовсе, либо считают равным  .
.



 (1)
(1)




