
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило сложения векторов по правилу треугольниковСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим два произвольных ненулевых вектора Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор Суммой векторов Кстати, если вектор Умножение вектора на число Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные». Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены. Обозначения: коллинеарность векторов записывают привычным значком параллельности: Произведением ненулевого вектора Правило умножения вектора на число легче понять с помощью рисунка:
9.Коллинеарные и компланарные векторы Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.\ Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны.Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Все выше упомянутые случаи легко рассмотреть, если разместить векторы на рёбрах параллелепипеда. 1. Любые два вектора находятся в одной плоскости, но в одной плоскости можно разместить и векторы AA1−→−, CC1−→− и AD−→−, то есть эти векторы компланарны. Также компланарны векторы AA1−→−, AB−→− и CC1−→−, так как два из этих векторов параллельны. Легко представить, что если привести их к общему началу, то вектор CC1−→− совпадет с вектором AA1−→−. 2. Например, векторы AB−→−, AD−→− и AA1−→− не компланарны, так как их нельзя разместить в одной и той же плоскости. Признак компланарности трёх векторов: Пусть векторы a⃗ и b⃗ не коллинеарны. Если для вектора c⃗ существует единственная пара реальных чисел x и y, такая, чтоc⃗ =x⋅a⃗ +y⋅b⃗, то векторы a⃗, b⃗ и c⃗ компланарны. Справедливо и обратное утверждение: Если три вектора a⃗, b⃗ и c⃗ компланарны и векторы a⃗ и b⃗ не коллинеарны, то вектор c⃗ можно разложить по векторам a⃗ и b⃗ одним единственным образом. 10. Координаты точки, координаты вектора Если даны две точки плоскости Если даны две точки пространства То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора. Обязательно нужно понимать различие между координатами точек и координатами векторов: Координаты точек – это обычные координаты в прямоугольной системе координат. Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя. Координаты же вектора – это его разложение по базису Записи координат точек и координат векторов вроде бы схожи:
11.Координаты суммы и разности векторов, произведение на число Сложение векторов (сумма векторов) a + b есть операция вычисления вектора c, все элементы которого равны попарной сумме соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен: сi = ai + bi Вычитание векторов (разность векторов) a - b есть операция вычисления вектора c, все элементы которого равны попарной разности соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен: сi = ai - bi В случае пространственной задачи сумму и разность векторов a = {ax; ay; az} и b = {bx; by; bz} можно найти воспользовавшись следующими формулами: a + b = {ax + bx; ay + by; az + bz} a - b = {ax - bx; ay - by; az - bz} Пример 3. Найти сумму векторов a = {1; 2; 5} и b = {4; 8; 1}. Решение: a + b = {1 + 4; 2 + 8; 5 + 1} = {5; 10; 6} Пример 4. Найти разность векторов a = {1; 2; 5} и b = {4; 8; 1}. Решение: a - b = {1 - 4; 2 - 8; 5 - 1} = {-3; -6; 4}
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 801; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.108.24 (0.008 с.) |

 и
и  :
:

 . Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору
. Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору  представляет собой вектор результирующего пути
представляет собой вектор результирующего пути  с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы.
с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы.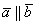 , при этом возможна детализация:
, при этом возможна детализация: 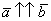 (векторы сонаправлены) или
(векторы сонаправлены) или  (векторы направлены противоположно).
(векторы направлены противоположно). является такой вектор
является такой вектор  , причём векторы
, причём векторы  и противоположно направлены при
и противоположно направлены при  .
.

 и
и  , то вектор
, то вектор  имеет следующие координаты:
имеет следующие координаты:
 и
и  , то вектор
, то вектор 
 , в данном случае
, в данном случае  . Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости
. Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости  , а смысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства
, а смысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства


