
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства векторного произведения векторов.Содержание книги Поиск на нашем сайте
1) Антикоммутативность (антиперестановочность) множителей
2) Ассоциативность (сочетательность) относительно скалярного множителя
3) Дистрибутивность (распределительность) относительно сложения (вычитания)
4) Если 5) Векторные произведения координатных ортов
Формулы (3.1) можно представить в виде следующей схемы (рис.3.2).
Рисунок 3.2
По схеме (3.2), векторное произведение двух соседних ортов в положительном направлении равно следующему орту в этом направлении, взятому со знаком плюс, а векторное произведение двух соседних ортов в отрицательном направлении равно следующему орту в этом направлении, взятому со знаком минус. Теорема. Если ненулевые векторы Кратко: if Доказательство. Если NB. Векторное произведение радиус-вектора
Выражение векторного произведения векторов через их координаты.
Теорема. Векторное произведение двух векторов, заданных своими координатами,
Доказательство. С учетом формул (3.1) получим
Следствие. Площадь параллелограмма, построенного на векторах Sпарал. = | Пример 1. Дано: А(1; 1; 1), В(2; 2; 2), С(4; 3; 5). Найти площадь треугольника SDABC и длину его высоты hB = | Решение. Пусть В Е
hB
D
Рисунок 3.3 Тогда С другой стороны, SD = Ответ: SD = Пример 2. Дано: Решение. Так как Ответ:
Смешанное произведение трех векторов.
Основные понятия.
Опр. Смешанное произведение трех векторов Теорема (геометрический смысл смешанного произведения). Смешанное произведение Доказательство. Построим параллелепипед, ребрами которого являются векторы
p - a
-
Рисунок 4.1.
Тогда для правой тройки векторов { Следствие 1. Ненулевые векторы Доказательство. 1) Необходимость. Если векторы 2) Достаточность. Если смешанное произведение Следствие 2. Смешанное произведение трех векторов, два из которых коллинеарны, равно нулю, так как такие векторы компланарны. Доказательство. Так как векторы свободные, то коллинеарные векторы параллельным переносом совмещаются с прямой. Оставшийся третий вектор переносится параллельно себе до пересечения с этой прямой и через них проводится плоскость. Следовательно, такие векторы компланарны. Fin.
|
||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 272; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.183.161 (0.007 с.) |

 ´
´  = -
= -  ×(
×(
 ) =
) =  или
или  ,
,  ,
,  соответственно равны:
соответственно равны: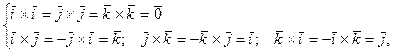 (3.1)
(3.1) (+)
(+) ;
;  (-)
(-)
 и силы
и силы  есть вектор момента силы
есть вектор момента силы 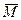 =
=  (3.2)
(3.2) -
-  +
+  =
=  (3.3)
(3.3) |.
|. = (1; 1; 1),
= (1; 1; 1),  = (3; 2; 4). Площадь треугольника SDABC равна половине площади параллелограмма, построенного на векторах
= (3; 2; 4). Площадь треугольника SDABC равна половине площади параллелограмма, построенного на векторах  SABЕC (рис.3.3).
SABЕC (рис.3.3).
 А С
А С =
=  ×
×  -
-  ×
×  +
+  ×
×  = 2
= 2  ´
´ 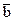 | =
| =  =
= 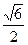
 =
= 
 ед.
ед.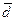 =
=  =
=  -
-  +
+  ) =
) =  = ±
= ±  = ± 13
= ± 13  = (-6; -24; 8),
= (-6; -24; 8),  = (6; 24; -8).
= (6; 24; -8). есть число, равное скалярному произведению вектора
есть число, равное скалярному произведению вектора  на вектор
на вектор  = (
= (


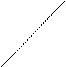




 h a
h a  Sосн.
Sосн.
 O
O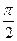 ]. Если {
]. Если { 


