
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Декартовы координаты вектора.Содержание книги Поиск на нашем сайте
Опр. Три ортогональные (взаимно перпендикулярные) координатные оси Ox, Oy, Oz, имеющие общее начало О и единую единицу масштаба, образуют декартову систему координат в пространстве (рис.1.9).
x
Рисунок1.9
Ось Ox - это ось абсцисс, ось Oy - это ось ординат, ось Оz - это ось аппликат. Орты Базисные тройки ортогональных ортов { Опр. Базисная тройка { Ориентация базисной тройки не меняется при циклической (круговой) перестановке ортов: { В научной литературе принято пользоваться правой базисной тройкой ортов {
Радиус-вектор точки и ее координаты.
Пусть М – произвольная точка пространства. Опр. Радиус-вектор точки М - это вектор
z
C
M
O
A
x Рисунок 1.10
Опустим из точки М перпендикуляры на координатные плоскости (Oxy), (Oxz) и (Oyz). Из рисунка 1.10 видно, что Опр. Декартовыми координатами радиус-вектора x = прx Таким образом, числа x, y, z называются декартовыми координатами (компонентами) радиус-вектора NB. Поскольку точка М имеет те же координаты, что и радиус-вектор
Радиус-вектор
Формула (1.6) называется разложением радиус-вектора Из теоремы Пифагора следует формула, выражающая длину радиус-вектора через его координаты | Так как радиус-вектор
Возводя в квадрат каждое из равенств (1.9) и почленно складывая их, получим сos2 NB. Из формул (1.8) следует, что координаты единичного вектора Пример. Радиус-вектор Решение. Найдем угол сos Координаты радиус-вектора x = | Ответ:
Декартовы координаты произвольного вектора на плоскости.
Найдем декартовые координаты произвольного вектора
yB B
yA A
x O xA
Рисунок 1.11
Проекции вектора прх Тогда Опр. Числа По теореме Пифагора имеем | Тогда по свойству проекции вектора на ось получим:
|
|||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 1296; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.8.172 (0.008 с.) |

 z
z





 y
y O
O =
=  с началом в начале декартовой системы координат – точке О, и концом – в точке М (рис.1.10).
с началом в начале декартовой системы координат – точке О, и концом – в точке М (рис.1.10).


 B y
B y
 = x×
= x×  = y×
= y×  = z×
= z×  1.7)
1.7) (1.8)
(1.8)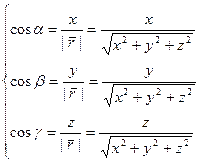 (1.9)
(1.9) равны его направляющим косинусам:
равны его направляющим косинусам:  ,
, 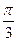 . Найти координаты радиус-вектора
. Найти координаты радиус-вектора  = ±
= ±  = ±0,5 Þ
= ±0,5 Þ 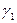 =
=  =
= 
 =
=  ; y = |
; y = | 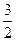 ; z1 = |
; z1 = |  = (
= ( = (
= ( =
=  на плоскости Oxy, если А(xA; yA), B(xB; yB) (рис.1.11).
на плоскости Oxy, если А(xA; yA), B(xB; yB) (рис.1.11). y
y






 =
=  на координатные оси Ох и Оу соответственно равны:
на координатные оси Ох и Оу соответственно равны: = хВ - хА; пру
= хВ - хА; пру  = уВ - уА
= уВ - уА +
+  = (хВ - хА)×
= (хВ - хА)×  = хВ - хА и
= хВ - хА и  = уВ - уА называются декартовыми координатами вектора
= уВ - уА называются декартовыми координатами вектора 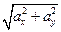 =
=  .
. Þ
Þ 



