
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Декартовы координаты произвольного вектора в пространстве.Содержание книги
Поиск на нашем сайте
Найдем декартовые координаты произвольного вектора
A
y
x Рисунок 1.12
Из определения разности векторов и формулы (1.6) получим
Следовательно, проекции вектора прх Опр. Числа NB. Каждая декартовая координата вектора численно равна его проекции на соответствующую ось. По свойству проекции вектора на ось имеем:
где (по теореме Пифагора) | | Пример 1. Найти координаты вектора Решение. Найдем ax = xB - xA = 5 -1 = 4; ay = yB - yA = 5; az = zB - zA = -3 Þ
Пример 2. Найти на оси Ох координаты точки М, которая равноудалена от точек А(2; -4; 6) и В(-3; 2; 5). Решение. По условию | | Так как |
Действия над векторами, заданными своими координатами.
Пусть
Линейные операции над векторами.
1) 2)
Условие равенства двух векторов.
Если
Условие коллинеарности двух векторов.
Если Следовательно, у коллинеарных векторов все проекции пропорциональны.
Пример. При каких значениях a и b векторы Решение. В данном случае равенство (1.15) примет вид: Деление отрезка в данном отношении.
Пусть в пространстве даны две различные точки М1(х1; y1; z1) и М2(x2; y2; z2) (рис.1.13). Найдем координаты точки М(x; y; z), которая делит отрезок [M1M2] в отношении
M1
О
x
Рисунок 1.13
Тогда: 1) если МÎ[M1M2], то говорят, что точка М делит отрезок [M1M2] внутренним образом. В этом случае 2) если МÏ[M1M2], то говорят, что точка М делит отрезок [M1M2] внешним образом. В этом случае 3) 4) если 5) если | Из равенства Þ где (x; y; z) – координаты точки М и радиус-вектора
Пример 1. Дано: М1(-3; 2; 4), М2(6; 0; 1). Определить координаты точки М(x; y; z), делящей отрезок [M1M2] в отношении Решение. Так как координаты точки М равны координатам ее радиус-вектора Ответ: М(3; Пример 2. Вычислить координаты точки М, делящей пополам вектор Решение. Так как точка М делит отрезок [M1M2] пополам, то Ответ: М(3; 1; 3). Пример 3. Даны две вершины треугольника АВС: А(5; 3), В(2; -1) и точка М(2; 2) пересечения его медиан. Определить координаты вершины С треугольника АВС (рис.1.14).
В
D М
А С
Рисунок 1.14
Решение. По условию точка D делит отрезок [AB] пополам. Тогда по формулам деления отрезка пополам найдем координаты точки D: хD = Согласно свойству пересечения медиан треугольника точка М делит отрезок [СD] в отношении Пример 4. Определить координаты концов отрезка [AB], если точки С(2; 0; 2) и D(5; -2; 0) делят его на три равные части (рис.1.15): А С D В
Рисунок 1.15 Решение. Точка С является серединой отрезка [АD], следовательно, хС = Аналогично, точка D является серединой отрезка [СВ], следовательно, хD = Ответ: А(-1; 2; 4); В(8; -4; -2). Скалярное произведение двух векторов.
Основные понятия.
Опр. Скалярное произведение двух векторов Таким образом, Так как |
Рисунок 2.1
NB. Механический смысл скалярного произведения. Если тело под действием постоянной силы
|
|||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 373; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |

 =
=  в пространстве, если А(хА; yA; zA), B(xB; yB; zB) (рис.1.12).
в пространстве, если А(хА; yA; zA), B(xB; yB; zB) (рис.1.12).




 z
z

 B
B
 O
O
 =
=  =
=  -
-  = (xB×
= (xB×  = хВ - хА, пру
= хВ - хА, пру  = уВ - уА, прz
= уВ - уА, прz  = zВ - zА.
= zВ - zА. (1.12) Þ
(1.12) Þ  , (1.13)
, (1.13) (1.14)
(1.14) + 5
+ 5  - 3
- 3  ; |
; |  =
= 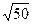 = 5
= 5  ;
; .
. | = |
| = |  |. Так как точка МÎОх Þ М(х; 0; 0). Поэтому
|. Так как точка МÎОх Þ М(х; 0; 0). Поэтому =
=  ; |
; |  | =
| =  =
=  .
. ×
×  ×
×  ×
×  =
=  ×
× 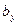 ×
×  ×
× 

 Þ
Þ  (1.15).
(1.15). Þ a = 1; b = -2.
Þ a = 1; b = -2. . Но так как деление векторов не определено, то воспользуемся эквивалентным соотношением
. Но так как деление векторов не определено, то воспользуемся эквивалентным соотношением 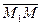 =
=  .
. z
z M
M



 М2
М2


 y
y Þ
Þ  Þ М1 = М2. А это противоречит условию, что точки М1 и М2 различны;
Þ М1 = М2. А это противоречит условию, что точки М1 и М2 различны; Þ
Þ  Þ
Þ  , (
, ( (1.17)
(1.17)
 ; 2)
; 2) , если М1(2; 8; 6), М2(4; -6; 0).
, если М1(2; 8; 6), М2(4; -6; 0). , Þ
, Þ  Þ М(3; 1; 3).
Þ М(3; 1; 3).
 ; уD =
; уD =  Þ D(
Þ D( ; 1)
; 1) . Следовательно, хМ =
. Следовательно, хМ =  Þ хС = хМ(1+
Þ хС = хМ(1+  Þ уС = уМ(1+
Þ уС = уМ(1+ 


 ; уС =
; уС =  ; zC =
; zC =  Þ
Þ  Þ А(-1; 2; 4).
Þ А(-1; 2; 4). ; уD =
; уD =  ; zD =
; zD =  Þ
Þ  Þ В(8; -4; -2)
Þ В(8; -4; -2) . (2.1)
. (2.1) и |
и |  (рис.2.1), то равенство (2.1) можно записать в следующем виде
(рис.2.1), то равенство (2.1) можно записать в следующем виде


 В С1
В С1
 А j B1 С
А j B1 С перемещается на расстояние
перемещается на расстояние  , то это значит, что над телом совершена механическая работа А, численно равная скалярному произведению силы
, то это значит, что над телом совершена механическая работа А, численно равная скалярному произведению силы 


