
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выражение смешанного произведения векторов через их координаты.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема. Смешанное произведение трех векторов, заданных своими координатами, равно определителю третьего порядка, составленному из координат перемножаемых векторов:
Доказательство.
+ cz ×
Следствие 1. Три вектора компланарны, если их смешанное произведение равно нулю.
Следствие 2. Объем параллелепипеда, построенного на трех векторах V = |
Следствие 3. Объем треугольной пирамиды, построенной на трех векторах Vпир. = Доказательство. Так как объем треугольной пирамиды равен
h
О
Рисунок 4.2
Пример 1. Найти объем треугольной пирамиды, если известны координаты ее вершин: А(1; 1; 1), В(4; 4; 4), С(3; 5; 5), D(2; 4; 7). Решение. Найдем координаты трех векторов, приведенных к общему началу, которые образуют ребра треугольной пирамиды АBСD. Например,
Пример 2. Даны координаты вершин треугольной пирамиды А(2; -4; 5), В(-1; -3; 4), С(5; 5; -1), D(1; -2; 2). Найти длину ее высоты hA, проведенной из вершины А. Решение. Найдем векторы
Рисунок 4.3 Обозначим С другой стороны Vпир.=
Приложение 1. Тема: «Векторная алгебра».
Точки А, В, С, D заданы координатами (см. таблицу).
Индивидуальная домашняя работа.
1) Найти координаты векторов 2) Найти координаты вектора 3) Найти координаты вектора 4) Найти координаты вектора 5) Проверить на линейную зависимость векторы 6) Вычислить скалярные произведения векторов 7) Найти проекции 8) В треугольнике АВС найти: а) площадь треугольника; б) длины всех сторон; в) длины всех высот; г) длины всех медиан; д) координаты точки пересечения медиан; е) все внутренние углы; ж) острый угол между медианой CМ и стороной АВ.
9) Вычислить векторные произведения векторов 10) Дано: 11) В треугольной пирамиде АBCD найти: а) ориентацию тройки векторов а) объем пирамиды; б) длины всех ребер; в) длины всех высот; г) площадь каждой грани пирамиды; д) углы между ребрами АВ и АС, АВ и АD, AC и AD. 12) Вычислить ( 13) Найти координаты вектора а) б) в) ТАБЛИЦА
0) А(-3; 1; -2); В(2; -2; 3); С(3; 2; -1); D(1; -3; -1). 1) A(-1; 2; 3); B(-3; -1; -2); C(2; 3; 1); D(-3; 2; 1). 2) A(1; 3; 2); B(2; -2; 3); C(-1; 2; -1); D(3; 2; 3). 3) A(2; -1; 1); B(-2; -3; 3); C(1; 3; 2); D(-1; -2; -3). 4) A(-1; 3; -1); B(2; -2; -1); C(1; -1; 2); D(-2; -2; -2). 5) A(-1; 1; 1); B(3; -3; 2); C(2; 3; 3); D(-3; -2; -1). 6) A(-3; 2; -1); B(2; -1; 2); C(3; 3; -1) D(1; 2; 3). 7) A(1; 2; 3); B(-1; -2; 3); C(3; 1; 2); D(1; -3; -2). 8) A(3; -1; 2); B(-2; -2; -2); C(1; 3; -2); D(-3; 3; -1). 9) A(-1; 3; 2); B(1; 2; -3); C(2; 1; 1); D(3; -1; 2). 10) A(1; -1; 1); B(-1; 2; 3); C(2; 1; -1); D(-2; -2; -3). 11) A(1; -2; 3); B(-2; 1; 3); C(3; -2; -1); D(1; 2; -2). 12) A(-1; 3; 2); B(1; -2; -1); C(2; 2; 1); D(-2; 1; -3). 13) A(-3; 1; 2); B(2; -2; -1); C(1; 2; 3); D(-2; -3; -3). 14) A(2; 3; 2); B(1; -2; 3); C(-1; -1; -2); D(-3; 2; 1). 15) A(-2; 2; 3); B(1; -1; -2); C(2; 3; 1); D(-3; -2; -1). 16) A(-2; 3; 1); B(1; -3; 2); C(3; -2; -1); D(2; 1; -3). 17) A(-3; -1; 2); B(2; 1; 3); C(3; 2; -3); D(-2; -2; -2). 18) A(2; -1; 3); B(-1; 3; 2); C(1; 2; -1); D(3; -2; -2). 19) A(1; 1; -3); B(2; -1; 2); C(-3; 2; 3); D(-2; -3; -2). 20) A(1; -3; 2); B(2; 3; 1); C(3; 2; -1); D(-2; -1; -2). 21) A(1; -2; 1); B(-2; 2; 1); C(2; 1; -1); D(-1; -3; -3). 22) A(1; 1; -2); B(2; 3; 1); C(-1; -2; -3); D(-2; 2; -1). 23) A(-2; 2; 2); B(3; -1; -2); C(1; 2; 3); D(-3; -2; 1). 24) A(-2; 1; -3); B(2; 3; 1); C(1; -2; 3); D(-3; -3; 2). 25) A(2; -2; 3); B(3; 3; 2); C(-2; -3; 1); D(-3; 2; 2). 26) A(2; -1; 2); B(3; 2; 3); C(-1; -2; -3); D(-3; -1; 1). 27) A(-2; -2; 3); B(1; -1; -1); C(2; 3; 1); D(3; -3; -2). 28) A(-2; -3; -1); B(1; -2; 1); C(2; 1; 2); D(-3; 3; -2). 29) A(-3; 2; -1); B(2; -1; 3); C(1; 1; -3); D(3; 3; 2). 30) A(2; 2; 3); B(-3; 1;-2); C(3; 1; 2); D(-2; -3; -1).
Требования к оформлению студентами индивидуальных домашних работ (ИДР).
1. Вариант ИДР должен соответствовать порядковому номеру фамилии студента в журнале его группы. 2. Каждая ИДР выполняется в отдельной ученической тетради чернилами любого цвета, кроме красного. В тетради должны быть поля для замечаний проверяющего, а в конце тетради должно быть несколько чистых листов для работы над ошибками в соответствии с замечаниями проверяющего. 3. Оформление обложки тетради должно соответствовать образцу: Индивидуальная домашняя работа по высшей математике на тему: Векторная алгебра студента (ки) гр. …….. Ф.И.О. ………………... вариант № …………… 4. Работа, выполненная по чужому варианту, не засчитывается. 5. Задачи и их решения располагаются в порядке возрастания их номеров в соответствии с нумерацией ИДР. 6. Условие задачи полностью переписывается с заменой общих данных на конкретные из своего варианта. 7. Решение задачи записывается аккуратно и подробно с необходимыми выкладками, чтобы было понятно, откуда что получено. 8. Незачтенная ИДР возвращается студенту для исправления ошибок. Студент должен в конце ИДР в работе над ошибками исправить их и вновь cдать ИДР на проверку. Студент, не выполнивший хотя бы одну ИДР, к экзамену не допускается.
Список рекомендуемой литературы
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. -М.: Наука, 1984. -320с. 2. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. -М.: Наука, 1971. – 232 с. 3. Бахвалов С.В. и др. Аналитическая геометрия. -М.: Просвещение, 1970. – 376 с. 4. Гурский Е.И. Основы линейной алгебры и аналитической геометрии. -Минск: Вышейш. шк., 1982. - 272с. 5. Гусак А.А. Высшая математика. Т.1. - Минск: ТетраСистемс, 2001. - 544с. 6. Письменный Д.Т. Конспект лекций по высшей математике. 1 часть. -М.: Рольф, 2000. - 288с. 7. Добротин Д.А. Основы линейной алгебры и аналитической геометрии. -Л.: Изд-во Ленингр. ун-та, 1977. - 120 с. 8. Лунгу К.Н. и др. Сборник задач по высшей математике. 1 курс. -М.: Айрис-пресс, 2003. -576с.
Оглавление
Стр.
1. Векторы………………………………………………………………………………………..1 1.1. Основные понятия…………………………………………………………………………..1 1.2. Линейные операции над векторами………………………………………………………..2 1.3. Линейная зависимость векторов…………………………………………………………...3 1.4. Линейно-векторное пространство. Базис. Разложение вектора по базису……………...5 1.5. Проекция вектора на ось……………………………………………………………………9 1.6. Декартовы координаты вектора………………..………………………………………….11 1.6.1. Радиус-вектор точки и ее координаты………………………………………………….11 1.6.2. Декартовы координаты произвольного вектора на плоскости.………………………13 1.6.3. Декартовы координаты произвольного вектора в пространстве.…………………….14 1.7. Действия над векторами, которые заданы своими координатами.…………………….15 1.8. Деление отрезка в данном отношении…………………………………………………...15 2. Скалярное произведение двух векторов……………………………………………………18 2.1. Основные понятия…………………………………………………………………………18 2.2. Свойства скалярного произведения векторов……………………………………………18 2.3. Выражение скалярного произведения векторов через их координаты………………...19 3. Векторное произведение двух векторов……………………………………………………20 3.1. Основные понятия…………………………………………………………………………20 3.2. Свойства векторного произведения векторов…………………………………………....21 3.3. Выражение векторного произведения векторов через их координаты ……………….22 4. Смешанное произведение трех векторов…………………………………………………...23 4.1. Основные понятия………………………………………………………………………….23 4.2. Свойства смешанного произведения векторов…………………………………………...24 4.3. Выражение смешанного произведения векторов через их координаты………………..25 Приложение 1. Индивидуальная домашняя работа по теме: «Векторная алгебра»…...…...28 Таблица…………………………………………………………..………………………………29 Требования к оформлению студентами индивидуальных домашних работ (ИДР)………...30 Список рекомендуемой литературы…………………………………………………………...31
|
||||||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 490; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.63.107 (0.009 с.) |

 =
=  (4.1)
(4.1) ´
´  )×
)×  =
=  ×
×  ×
×  -
-  ×
×  +
+  ×
×  )×(cx×
)×(cx×  модуля их смешанного произведения.
модуля их смешанного произведения.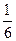 |
|  произведения площади ее основания на высоту, то Vпир. =
произведения площади ее основания на высоту, то Vпир. =  SОАDВ × h =
SОАDВ × h = 



 С
С
 = (3; 3; 3),
= (3; 3; 3),  = (2; 4; 4),
= (2; 4; 4),  = (1; 3; 6). Тогда
= (1; 3; 6). Тогда








 Vпир. =
Vпир. =  =
=  -1 = 6×
-1 = 6×  = =6×
= =6×  = = 6×1×1×3 = 18} =
= = 6×1×1×3 = 18} =  = 3 (ед3.). Ответ: Vпир. = 3 (ед3.)
= 3 (ед3.). Ответ: Vпир. = 3 (ед3.) ,
, 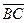 ,
,  и по формуле (4.4) определим объем V пирамиды (рис.4.3).
и по формуле (4.4) определим объем V пирамиды (рис.4.3).


 А
А
 D
D В С
В С =
=






 =
=  =
=  . Найдем
. Найдем  -3 =
-3 = 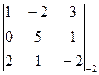 =
=  =
=  = -45
= -45
 =
=  -
-  +
+  = -11
= -11  =
=  = 15. Тогда hA =
= 15. Тогда hA =  = 3. Ответ: hA = 3 ед.
= 3. Ответ: hA = 3 ед.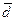 =
=  =
=  . Посчитать их длины |
. Посчитать их длины |  ,
,  ,
,  ,
,  ,
,  .
. ||
||  =
=  , если известно, что
, если известно, что  ,
,  ,
,  ,
, 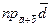 ,
,  .
. =
=  =
=  =
=  = |
= | 


