
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение векторов и умножение вектора на числоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приложения Аналитическая геометрия. Геометрические векторы (Примерное содержание одной из глав будущего учебного пособия)
Основные понятия Геометрическим вектором называется направленный отрезок, который можно перемещать параллельно ему самому. Направленный отрезок с началом в точке A и концом в точке B обозначается Таким образом, два направленных отрезка Всегда выражение «вектор AB » означает вектор, изображаемый направленным отрезком AB. Длиной (или модулем) вектора Вектор Вектор, длина которого равна 1, называется единичным. Единичный вектор, направление которого совпадает с направлением вектора AB, называется ортом вектора AB и обозначается Углом между векторами Векторы, лежащие на параллельных или совпадающих прямых, называются коллинеарными. Векторы, лежащие в параллельных или совпадающих плоскостях, называются компланарными. Если угол между векторами равен Сложение векторов и умножение вектора на число
Суммой векторов Произведением вектора Операции сложения векторов и умножения вектора на число называются линейными операциями. Свойства линейных операций с векторами Для любых векторов
Условие коллинеарности векторов: два ненулевых вектора Нулевой вектор считается коллинеарным любому вектору.
Скалярное произведение векторов
Скалярным произведением векторов Свойства векторного произведения векторов Для любых векторов
1. 2.
Условие коллинеарности векторов: два вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т.е.
(нулевой вектор можно считать коллинеарным любому вектору). Смешаное произведение векторов
Смешанным произведением векторов
т.е. векторное произведение двух векторов По определению скалярного и векторного произведений имеем ( причем знак (+) берется в том случае, когда угол θ острый, т.е. тройка векторов Геометрический смысл смешанного произведения: смешанное произведение векторов Контрольная работа Класс «Аналитическая геометрия». Угол прямой с плоскостью. (Из примерного содержания методического пособия для учителя)
1. В основании прямого параллелепипеда АВСДА1 В1 С1 Д1 лежит параллелограмм с углом при вершине А равным 600. Отношение ребер АВ: АД: АА = 1: 2: 3. Найдем угол между прямой В1 Д и плоскостью грани АА1 Д Д1. 2. В основании пирамиды SABC лежит равнобедренный треугольник с прямым углом С. Каждое боковое ребро образует с плоскостью основания угол, равный 450. На ребре SB взята точка М – середина этого ребра. Найдем угол между прямой АМ и плоскостью грани SBC. 3. В правильной призме АВСА1 В1 С1 угол между прямыми АВ и АС равен 2а. Найдем угол между прямой ВС и плоскостью грани АСС1 А. 4. В основании прямой призмы АВСА1 В1 С1 лежит равнобедренный треугольник с прямым углом при вершине С. Высота призмы равна катету основания. На ребрах АВ, СС, АС взяты соответственно точки Р, Q, R – середины этих ребер. Построим сечение призмы плоскостью, проходящей через вершину С, параллельно прямой РQ и В R и найдем угол, который образует с секущей плоскостью прямая СВ. 5. На ребрах А В и ДД куба АВСД А1 В1 С1 Д1 взяты соответственно точки P и Q – середины этих ребер. Найдем угол, который образует прямая В1 Д с секущей плоскостью а, проходящей через вершину С, перпендикулярно прямой PQ. Построим сечение куба плоскостью а и найдем точку пересечения прямой PQ с плоскостью а.
Контрольная работа Контрольная работа Класс I вариант.
1. На ребрах A1B1 и BC куба ABCDA1B1C1D1 взяты соответственно точки P и Q – середины этих ребер. Считая ребро куба равным a, найдите расстояния до прямой PQ от следующих точек: C1; б) D1; в) D. 2. На ребре C1D1 куба ABCDA1B1C1D1 взята точка P – середина этого ребра. Считая ребро куба равным a, найдите расстояния до плоскости BDP от следующих точек: A1; б) A; в) C1. 3. На ребрах AB, CC1 и С1D1 куба ABCDA1B1C1D1 взяты соответственно точки P, Q и R – середины этих ребер. Считая ребро куба равным а, найдите расстояния между прямой B1D1 и следующими прямыми: DP; б) DQ; в) DR. 4. В правильной призме ABCDA1B1C1D1 угол между прямыми BD1 и B1D равен 90о. Найдите углы, которые образует прямая B1D со следующими прямыми: AA1; б) A1C; в) CD1. 5. На ребре СС1 правильной призмы ABCDA1B1C1D1, боковое ребро которой в два раза больше стороны основания, взяты точки Е1, Е2 и Е3 – такие, что СЕ1=Е1Е2=Е2Е3=Е3С1, а на ребре CD взята точка К – середина этого ребра. Найдите углы, которые образуют с плоскостью АА1К следующие прямые: DE1; б) DE2; в) DE3. 6. Основанием пирамиды MABCD является прямоугольник, а ее боковое ребро MB перпендикулярно плоскости основания и АВ: AD: МВ=1:2:1. На ребрах АD и АВ взяты соответственно точки K и L – середины этих ребер. Найдите следующие двугранные углы: а) MCLB; б) MACB; в)MCKB.
Список литературы для учащихся
1. Александров А.Д. и др. Геометрия 10-11 класс. - М.: «Просвещение», 1992. 2. Атанасян Л.С. и др. Геометрия 10-11 класс. - М.: «Просвещение», 1993. 3. Бевз Г.П. и др. Геометрия 10-11 класс. - М.: «Просвещение», 1994. 4. Жафяров А.Ж. Аналитическая геометрия. - Новосибирск, 1993. 5. Звавич Л.И. и др. Геометрия. 8-11 классы. Пособие для школ и классов с углубленным изучением математики. – М.: «Дрофа», 2000 6. Земляков А.Н. Геометрия в 9 классе. - М.: «Просвещение», 1988. 7. Зив Б.Г. «Дидактические материалы по геометрии 10 класс». - М.: «Просвещение», 2000. 8. Зив Б.Г. «Дидактические материалы по геометрии 11 класс». - М.: «Просвещение», 2000. 9. Зив Б.Г. «Задачи по геометрии 7-11 класс». - М.: «Просвещение», 2000. 10. Клетеник Д.В. Сборник задач по Аналитической геометрии. - М.: «Наука», 1986. 11. Марков Л.Н. и др. Основы Аналитической геометрии. - Минск: «Амалфея», 1999. 12. Погорелов. Геометрия 10 -11 класс. - М.: «Просвещение», 1992. 13. Погорелов А.В., Основания А.В. Геометрии. - М.: «Наука», 1977. 14. Энциклопедия для детей «Аванта+». Том 11. Математика. - М.: «Аванта», 1998.
Список литературы для учителя
1. Александров А.Д. и др. Геометрия 10-11 класс. - М.: «Просвещение», 1992. 2. Атанасян Л.С. и др. Геометрия 10-11 класс. - М.: «Просвещение», 1993. 3. Бевз Г.П. и др. Геометрия 10-11 класс. - М.: «Просвещение», 1994. 4. Жафяров А.Ж. Аналитическая геометрия. - Новосибирск, 1993. 5. Звавич Л.И. и др. Геометрия. 8-11 классы. Пособие для школ и классов с углубленным изучением математики. - М.: «Дрофа», 2000. 6. Земляков А.Н. Геометрия в 9 классе. - М.: «Просвещение», 1988. 7. Зив Б.Г. «Дидактические материалы по геометрии 10 класс». - М.: «Просвещение», 2000. 8. Зив Б.Г. «Дидактические материалы по геометрии 11 класс». - М.: «Просвещение», 2000. 9. Зив Б.Г. «Задачи по геометрии 7-11 класс». - М.: «Просвещение», 2000. 10. Клетеник Д.В. Сборник задач по Аналитической геометрии. - М.: «Наука», 1986. 11. Марков Л.Н. и др. Основы Аналитической геометрии. – Минск: «Амалфея», 1999. 12. Погорелов А.В. Геометрия 10-11 класс. - М.: «Просвещение», 1992. 13. Погорелов А.В. Основания геометрии. - М.: «Наука», 1977. 14. Поповский и др. «Улубленное изучение геометрии в 10-11 классе. - М.: «Просвещение», 2002. 15. Энциклопедия для детей «Аванта+». Том 11. Математика. М. «Аванта». 1998 16. Вебер Н.П. Информационная компетенция. – «Гимназия № 1 г. Нерюнгри», 2004. 17. Вебер Н.П. Учебно-воспитательная компетенция. - «Гимназия № 1 г. Нерюнгри», 2004. 18. Сизонова В.Г., Фатькина Н.Н. Коммуникативная компетенция. – «Гимназия № 1 г. Нерюнгри», 2004. Приложения Аналитическая геометрия. Геометрические векторы (Примерное содержание одной из глав будущего учебного пособия)
Основные понятия Геометрическим вектором называется направленный отрезок, который можно перемещать параллельно ему самому. Направленный отрезок с началом в точке A и концом в точке B обозначается Таким образом, два направленных отрезка Всегда выражение «вектор AB » означает вектор, изображаемый направленным отрезком AB. Длиной (или модулем) вектора Вектор Вектор, длина которого равна 1, называется единичным. Единичный вектор, направление которого совпадает с направлением вектора AB, называется ортом вектора AB и обозначается Углом между векторами Векторы, лежащие на параллельных или совпадающих прямых, называются коллинеарными. Векторы, лежащие в параллельных или совпадающих плоскостях, называются компланарными. Если угол между векторами равен Сложение векторов и умножение вектора на число
Суммой векторов Произведением вектора Операции сложения векторов и умножения вектора на число называются линейными операциями.
|
||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 497; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.148.222 (0.01 с.) |

 . Векторы обозначаются строчными латинскими буквами со стрелками:
. Векторы обозначаются строчными латинскими буквами со стрелками: 
 , имеющие одинаковые длины и направления, изображают один и тот же вектор
, имеющие одинаковые длины и направления, изображают один и тот же вектор  , и именно в этом смысле мы будем писать равенства между векторами и направленными отрезками:
, и именно в этом смысле мы будем писать равенства между векторами и направленными отрезками: 
 называется расстояние между точками A и B. Будем считать, что единица измерения длин выбрана и, говоря о длинах отрезков, не будем указывать, какой единицей они измеряются. Модуль вектора AB обозначается символом
называется расстояние между точками A и B. Будем считать, что единица измерения длин выбрана и, говоря о длинах отрезков, не будем указывать, какой единицей они измеряются. Модуль вектора AB обозначается символом  ,
, , равный по длине вектору
, равный по длине вектору  .
. называется угол
называется угол  (0 ≤
(0 ≤  , то векторы называются ортогональными.
, то векторы называются ортогональными. называется вектор
называется вектор  с началом в точке A и концом в точке C (правило треугольника).
с началом в точке A и концом в точке C (правило треугольника). называется вектор
называется вектор 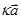 , модуль, которого равен
, модуль, которого равен 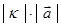 , направление совпадает с направлением вектора
, направление совпадает с направлением вектора  и противоположно направлению вектора
и противоположно направлению вектора  (рис.2). При
(рис.2). При  произведение
произведение 
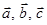 и любых чисел α, β:
и любых чисел α, β:
 коллинеарны тогда и только тогда, когда они пропорциональны, т.е. существует число (
коллинеарны тогда и только тогда, когда они пропорциональны, т.е. существует число (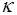 ) такое, что
) такое, что  .
. и равное произведению их модулей и косинуса угла
и равное произведению их модулей и косинуса угла  между ними, т.е.
между ними, т.е. 
 и любых чисел α, β:
и любых чисел α, β: , т.е. векторное произведение антикоммутативно;
, т.е. векторное произведение антикоммутативно; , т.е. векторное произведение дистрибутивно относительно сложения;
, т.е. векторное произведение дистрибутивно относительно сложения; , т.е. векторное произведение ассоциативно относительно вещественного множителя.
, т.е. векторное произведение ассоциативно относительно вещественного множителя.
 ) и определяемое равенством
) и определяемое равенством ,
,
 умножается скалярно на третий вектор
умножается скалярно на третий вектор  .
. ) = (
) = ( = =
= =  ,
, — угол между векторами
— угол между векторами  , а
, а  — угол между векторами (
— угол между векторами ( ) и
) и 


