
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторы и линейные операции над векторами. Разложение векторовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тема 3. Векторная алгебра Действия над векторами, заданными своими координатами Определение 3.4 Проекцией вектора Точки
Основные свойства проекции: 1) 2) 3) 4) Рассмотрим в пространстве прямоугольную систему координат
Единичные векторы Произвольный вектор
а значит, существуют числа
Следовательно, вектор
Формула (3.5) называется разложением вектора Векторное равенство (3.5) записывают в виде
Имеет место аналогичное разложение вектора
Длина вектора
Для плоского вектора
Направление вектора
Справедливо равенство
При выполнении линейных операций над векторами тем же операциям подвергнутся и их проекции на координатные оси. Пусть даны два вектора При сложении векторов их одноименные координаты складываются, при вычитании – вычитаются, при умножении на число – умножаются на это число:
Векторы
Векторы
Радиус-вектором точки Координаты точки – это координаты её радиус-вектора Для вектора
Здесь Деление отрезка в данном отношении Определим радиус-вектор Вектор откуда Из равенства векторов (3.16) следуют три координатных формулы
Для
Скалярное произведение векторов Определение 3.5 Скалярным произведением двух ненулевых векторов Таким образом
где
Из рисунка видно:
С учетом (3.20) можно записать равенства
Свойства скалярного произведения: 1) 2) 3) 4) 5) Условие перпендикулярности векторов. Если векторы В частности
Приложения скалярного произведения С помощью скалярного произведения определяют косинус угла между векторами по формуле:
или переходя к координатам векторов
Находят проекцию одного вектора на направление другого по формуле:
Определяют длину вектора
Приложение векторного произведения Площадь параллелограмма, построенного на векторах
а площадь треугольника, построенного на векторах
Тема 3. Векторная алгебра Векторы и линейные операции над векторами. Разложение векторов Определение 3.1 Вектором (геометрическим вектором) называется направленный отрезок, то есть отрезок, имеющий определенную длину и направление. Векторы рассматриваются на плоскости (двумерные) и в пространстве (трехмерные). И в том, и в другом случае вектор определяется упорядоченной парой точек, первая из которых – начало вектора, другая – конец вектора. Для обозначения векторов используются символы
Длиной или модулем Нулевым вектором называется вектор, начало и конец которого совпадают. Нуль-вектор обозначается символом Единичным вектором называет вектор, длина которого равна единице. Единичный вектор, направление которого совпадает с направлением вектора Два ненулевых вектора называются равными, если один из них путем параллельного переноса можно совместить с другим так, что совпадут их начала и концы (рис 1.2). Обозначают
С точки зрения векторной алгебры вектор не меняется при его параллельном переносе с сохранением его длины и его направления, то есть точку приложения вектора можно помещать в любую точку пространства. Такие векторы называются свободными. Линейными операциями над векторами называются операции сложение, вычитание и умножение вектора на число. Сложение двух векторов
Для построения суммарного вектора Суммой двух векторов
При этом ясно, что результат сложения не зависит от того, в какой точке пространства начало первого слагаемого: при её изменении весь треугольник параллельно переносится. Это правило сложения векторов называется правилом треугольника. Сложение многих векторов Непосредственно видно, что получается следующее правило для сложения векторов. Правило многоугольника. Суммой нескольких векторов является вектор, соединяющий начало первого слагаемого вектора с концом последнего при условии, что начало каждого последующего вектора совмещено с концом предыдущего (рис. 3.6).
Законы сложения векторов: 1. 2. 3. Разностью двух векторов
Заметим, что если на векторах Произведением ненулевого вектора
Законы умножения вектора на число: 1. 2. 3. 4. Из определения произведения вектора на число следует, что всякий вектор
Если над векторами
представляющий собой линейную комбинацию исходных векторов. Векторы
где скалярные коэффициенты Если все коэффициенты равны нулю, то соотношение (3.2) будет выполняться, но оно не будет устанавливать зависимости между векторами. Про векторы Понятие линейной независимости между векторами используется для алгебраической характеристики взаимного расположения векторов в пространстве. Определение 3.2 Два ненулевых вектора Коллинеарные векторы могут быть одинаково направленными (как векторы
Теорема 3.1 Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Следствие. Если между двумя неколлинеарными векторами выполняется равенство
то оба коэффициента должны равняться нулю Определение 3.3 Ненулевые векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Любые два вектора всегда компланарны, а три вектора могут и не быть компланарными. Теорема 3.2 Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Представление вектора Рассмотрим произвольный вектор Теорема 3.3 Каждый вектор
Из (3.4) следует, что любые четыре вектора в пространстве линейно зависимы. Упорядоченная тройка некомпланарных (линейно независимых) векторов Аналогично: упорядоченная пара
3 .2 Прямоугольные координаты вектора.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 729; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.107 (0.01 с.) |

 на ось
на ось  называется число, равное длине вектора
называется число, равное длине вектора  (рис. 3.9), взятое со знаком «плюс», если направление вектора
(рис. 3.9), взятое со знаком «плюс», если направление вектора  - это точки пересечения оси
- это точки пересечения оси 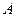 и
и  , перпендикулярно оси
, перпендикулярно оси  .
.
 , где
, где 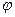 - угол между вектором
- угол между вектором  и осью
и осью  ;
;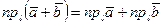 ;
; .
.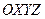 . Построим на координатных осях
. Построим на координатных осях  и
и  единичные векторы, обозначаемые
единичные векторы, обозначаемые  соответственно (рис. 3.10).
соответственно (рис. 3.10).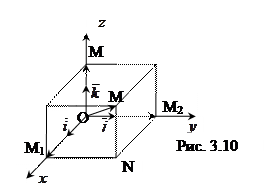
 вектора
вектора  ,
, 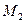 и
и  точки пересечения этих плоскостей с осями
точки пересечения этих плоскостей с осями 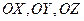 соответственно. Тогда
соответственно. Тогда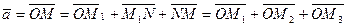 ,
, ,
,  ,
,  .
. , такие что
, такие что ,
, 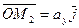 ,
,  и
и ,
,  ,
, 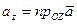 .
.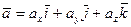 . (3.5)
. (3.5) . Коэффициенты
. Коэффициенты 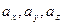 линейной комбинации (3.5) называют прямоугольными координатами вектора
линейной комбинации (3.5) называют прямоугольными координатами вектора  (3.6)
(3.6) на плоскости (рис. 3.11).
на плоскости (рис. 3.11).
 . (3.7)
. (3.7) определяется по формуле
определяется по формуле . (3.8)
. (3.8)
 . (3.9)
. (3.9) - углы, которые составляет вектор
- углы, которые составляет вектор  ,
, 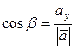 ,
, 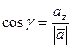 . (3.10)
. (3.10)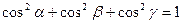 . (3.11)
. (3.11) и
и 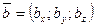 .
. , (3.12)
, (3.12) .
. равны тогда и только тогда, когда равны их соответствующие координаты:
равны тогда и только тогда, когда равны их соответствующие координаты: ,
, 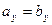 ,
,  . (3.13)
. (3.13) . (3.14)
. (3.14)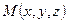 называется вектор
называется вектор  (рис. 3.12), начало которого совпадает с началом координат, а конец с точкой
(рис. 3.12), начало которого совпадает с началом координат, а конец с точкой 

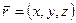 .
. , заданного координатами точки
, заданного координатами точки  и
и  , его координаты определяются из векторного равенства
, его координаты определяются из векторного равенства (3.15)
(3.15) и
и  - радиус-векторы точек
- радиус-векторы точек 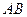 равны разностям одноименных координат конечной
равны разностям одноименных координат конечной  точки
точки  .
.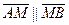 и одинаково направлен с
и одинаково направлен с  , поэтому
, поэтому  . Учитывая векторные равенства
. Учитывая векторные равенства  ,
,  получим
получим  ,
, (3.16)
(3.16) ,
,  ,
,  . (3.17)
. (3.17) (
( ,
, 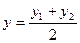 ,
,  . (3.18)
. (3.18) , равное произведению длин этих векторов на косинус угла
, равное произведению длин этих векторов на косинус угла 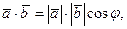 (3.19)
(3.19)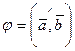 .
.
 ,
, 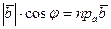 . (3.20)
. (3.20) . (3.21)
. (3.21) (коммутативный закон);
(коммутативный закон); (дистрибутивный закон);
(дистрибутивный закон); (ассоциативный по отношению к скалярному множителю);
(ассоциативный по отношению к скалярному множителю); , скалярный квадрат вектора
, скалярный квадрат вектора  .
.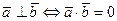 (3.22)
(3.22)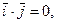

 .
. , (3.24)
, (3.24)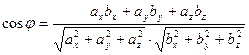 . (3.25)
. (3.25) ,
,  . (3.26)
. (3.26) . (3.27)
. (3.27) (3.32)
(3.32) (3.33)
(3.33) ,
,  . Если
. Если  с началом в точке
с началом в точке 
 вектора
вектора  . Модуль нулевого вектора равен нулю.
. Модуль нулевого вектора равен нулю. .
. .
.
 и построить на них как на сторонах параллелограмм, то вектор
и построить на них как на сторонах параллелограмм, то вектор  , идущий из общего начала
, идущий из общего начала  (рис. 3.3).
(рис. 3.3).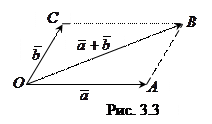
 , достаточно построить треугольник
, достаточно построить треугольник  . Сформулированное правило определения суммы можно заменить более удобным.
. Сформулированное правило определения суммы можно заменить более удобным.
 ,
,  ,
,  прибавляется вектор
прибавляется вектор 

 ,
, ,
, .
.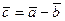 , который при сложении с вектором
, который при сложении с вектором 
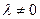 называется вектор
называется вектор 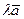 (или
(или  ), длина которого равна
), длина которого равна  , а направление совпадает с направлением вектора
, а направление совпадает с направлением вектора  и противоположно ему при
и противоположно ему при  .
. Например, если дан вектор
Например, если дан вектор  , то векторы
, то векторы  и
и  имеют вид
имеют вид 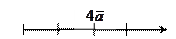 и
и 
 .
. ,
, ,
, ,
, .
. (3.1)
(3.1) ,
,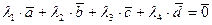 , (3.2)
, (3.2) не все равны нулю.
не все равны нулю.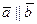 ), если они лежат на одной прямой или на параллельных прямых.
), если они лежат на одной прямой или на параллельных прямых.

 ,
, .
. - коллинеарны
- коллинеарны 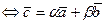 (3.3)
(3.3)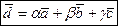 (3.4)
(3.4)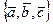 называется базисом во множестве геометрических векторов пространства. Скалярные коэффициенты
называется базисом во множестве геометрических векторов пространства. Скалярные коэффициенты 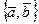 неколлинеарных (линейно независимых) векторов образует базис геометрических векторов на плоскости. Коэффициенты
неколлинеарных (линейно независимых) векторов образует базис геометрических векторов на плоскости. Коэффициенты  в разложении (3.4) есть координаты вектора
в разложении (3.4) есть координаты вектора 


