
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Базис и размерность линейного векторного пространстваСодержание книги
Поиск на нашем сайте
Множество векторов Понятие линейной независимости распространяется на бесконечные системы векторов. Такая система называется линейно независимой, если линейно независима любая ее конечная часть. Базис линейного векторного пространства
относительно базисных векторов В конечномерном векторном пространстве a) каждое множество из b) никакое множество из c) каждое множество из Упорядоченная совокупность чисел Из каждой линейно независимой системы векторов можно построить путем линейных комбинаций (процессом ортогонализации) систему попарно ортогональных единичных векторов
Такую систему векторов называют ортонормированной (ортогональной нормированной) системой. В конечномерном унитарном векторном пространстве размерности Конечномерные действительные унитарные векторные пространства называются евклидовыми векторными пространствами (обозначение
Пример. Рассмотрим множество матриц – столбцов
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.131.51 (0.006 с.) |

 ,
,  , …,
, …,  называется линейно независимым, если равенство
называется линейно независимым, если равенство  выполняется лишь при
выполняется лишь при  . В противном случае векторы
. В противном случае векторы  не равный нулю) может быть выражен в виде линейной комбинации
не равный нулю) может быть выражен в виде линейной комбинации  остальных векторов
остальных векторов 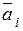 этого множества.
этого множества. есть такое множество линейно независимых векторов
есть такое множество линейно независимых векторов  ,
, 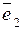 , …,
, …,  пространства
пространства 

 (1.2.16)
(1.2.16) (
( =1, 2, …,
=1, 2, …,  ). Любая система линейно независимых векторов образует базис линейного векторного пространства, состоящего из всевозможных линейных комбинаций этих векторов. Число
). Любая система линейно независимых векторов образует базис линейного векторного пространства, состоящего из всевозможных линейных комбинаций этих векторов. Число  , порожденном
, порожденном  векторов не является базисом;
векторов не является базисом; векторов необходимо линейно зависимо.
векторов необходимо линейно зависимо. в представлении (1.2.16) вектора
в представлении (1.2.16) вектора 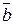 имеет координаты
имеет координаты  , а вектор
, а вектор  –
– 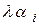 (
( (1.2.17)
(1.2.17) ,
,  , …,
, …,  .
. , где
, где  ). Система базисных единичных векторов
). Система базисных единичных векторов 
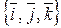 образует ортонормированный базис этого пространства. Множество векторов на обычной плоскости представляют евклидово пространство
образует ортонормированный базис этого пространства. Множество векторов на обычной плоскости представляют евклидово пространство  .
. размера
размера  . Сравнение определенных ранее линейных операций сложения матриц и умножения матриц на число (скаляр) с определяющими свойствами линейного векторного пространства позволяет сделать вывод, что множество матриц – столбцов образует векторное пространство, в котором в качестве векторов выступают эти матрицы. Это векторное пространство становится унитарным, если в нем определить скалярное произведение двух матриц – столбцов (векторов)
. Сравнение определенных ранее линейных операций сложения матриц и умножения матриц на число (скаляр) с определяющими свойствами линейного векторного пространства позволяет сделать вывод, что множество матриц – столбцов образует векторное пространство, в котором в качестве векторов выступают эти матрицы. Это векторное пространство становится унитарным, если в нем определить скалярное произведение двух матриц – столбцов (векторов)  (
( ) и
) и  (
( ) как
) как 
 , где символом
, где символом 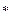 обозначена операция транспонирования матрицы, а произведение находится по правилу умножения матриц. Это пространство является и нормированным, т. к. позволяет ввести норму матрицы – столбца
обозначена операция транспонирования матрицы, а произведение находится по правилу умножения матриц. Это пространство является и нормированным, т. к. позволяет ввести норму матрицы – столбца 
 .
. ,
,  ,
, ,
,  ,
, ,
,  ,
,
 (
(


