Лекция 3.1.2 «Основные теоремы дифференциального начисления. Правило Лопиталя»
Учебные вопросы:
1. Основные теоремы дифференциального начисления
2. Раскрытие неопределенностей. Правило Лопиталя
Основные теоремы дифференциального начисления
Теорема Ролля
Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале (а, b) существует точка e, a < e < b, в которой производная функция f(x) равная нулю, f¢(e) = 0.
Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка e такая, что в соответствующей точке кривой y = f (x) касательная параллельна оси О х. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.
Теорема Ролля имеет несколько следствий:
1) Если функция f (x) на отрезке [ a, b ] удовлетворяет теореме Ролля, причем f (a) = f (b) = 0, то существует по крайней мере одна точка e, a < e < b, такая, что f ¢(e) = 0, т. е. между двумя нулями функции найдется хотя бы одна точка, в которой производная функции равна нулю.
2) Если на рассматриваемом интервале (а, b) функция f (x) имеет производную (n -1)- го порядка и n раз обращается в нуль, то существует по крайней мере одна точка интервала, в котором производная (n – 1)- го порядка равна нулю.
Теорема Лагранжа.
Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b), то на этом интервале найдется по крайней мере одна точка e
a < e < b, такая, что 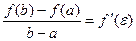 . .
Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.
Рассмотренная выше теорема Ролля является частным случаем теоремы Лагранжа.
Отношение 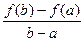 равно угловому коэффициенту секущей АВ. равно угловому коэффициенту секущей АВ.
 у у
В
А
0 а e b x
Если функция f (x) удовлетворяет условиям теоремы, то на интервале (а, b) существует точка e такая, что в соответствующей точке кривой y = f (x) касательная параллельна секущей, соединяющей точки А и В (см. рис.). Таких точек может быть и несколько, но одна существует точно.
Определение. Выражение
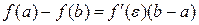
называется формулой Лагранжа или формулой конечных приращений.
Иногда формулу Лагранжа записывают в несколько другом виде:
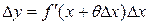 , ,
где 0 < q < 1, D x = b – a, Dy = f (b) – f (a).
Теорема Коши
Если функции f(x) и g(x) непрерывны на отрезке [a, b] и дифференцируемы на интервале (a, b) и g¢(x) ¹ 0 на интервале (a, b), то существует по крайней мере одна точка e, a < e < b, такая, что
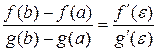 , ,
т. е. отношение приращений функций на данном отрезке равно отношению производных в точке e.
Следует отметить, что рассмотренная выше теорема Лагранжа является частным случаем (при g (x) = x) теоремы Коши.
Теорема Ферма. Если дифференцируемая на промежутке X функция  достигает наибольшего или наименьшего значения во внутренней точке достигает наибольшего или наименьшего значения во внутренней точке 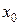 этого промежутка, то производная функции в этой точке равна нулю, т.е. этого промежутка, то производная функции в этой точке равна нулю, т.е. 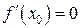 . .
|