Приведение исходной системы к виду, удобному для применения сходящегося итерационного процесса
Похожие статьи вашей тематики
Теорема сходимости итерационного процесса накладывает жесткие условия на коэффициенты системы (4.3). Однако, если  , то с помощью элементарных преобразований системы (4.3) ее можно заменить эквивалентной системой , то с помощью элементарных преобразований системы (4.3) ее можно заменить эквивалентной системой  , такой, что условия теоремы сходимости будут выполнены. , такой, что условия теоремы сходимости будут выполнены.
Умножим левую и правую часть соотношения (4.3) слева на матрицу  , где , где  - матрица с малыми по модулю элементами. - матрица с малыми по модулю элементами.
Проведем преобразования:

Если обозначить  , ,  , то получим , то получим  . .
Если элементы матрицы 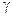 достаточно малы по модулю, т.е. ú достаточно малы по модулю, т.е. ú  , то элементы матрицы , то элементы матрицы  будут удовлетворять достаточному условию сходимости итерационного процесса. будут удовлетворять достаточному условию сходимости итерационного процесса.
Итерационный процесс заканчивается, если для двух приближений  и и  выполнено условие выполнено условие  , где , где  - заданная точность. - заданная точность.
2. Метод Зейделя
 Метод Зейделя представляет собой некоторую модификацию метода простых итераций. Основная его идея состоит в том, что при вычислении Метод Зейделя представляет собой некоторую модификацию метода простых итераций. Основная его идея состоит в том, что при вычислении  -го приближения неизвестной -го приближения неизвестной  учитываются уже вычисленные ранее учитываются уже вычисленные ранее  -е приближения неизвестных -е приближения неизвестных  . Т.е. найденное . Т.е. найденное  -е приближение сразу же используется для получения -е приближение сразу же используется для получения  -го приближения последующих координат (Рис.4.1). -го приближения последующих координат (Рис.4.1).
Предполагая, что  -е приближения -е приближения  корней системы (4.4) известны, корней системы (4.4) известны,  -е приближения корней будут находиться по следующим итерационным формулам метода Зейделя: -е приближения корней будут находиться по следующим итерационным формулам метода Зейделя:
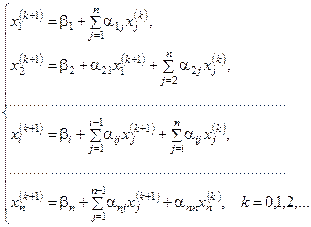 . (4.8) . (4.8)
Теорема 4.3 (достаточное условие сходимости метода Зейделя).
Если для приведенной системы  выполнено хотя бы одно из условий: выполнено хотя бы одно из условий:
1)  , где , где 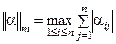 ; ;
2)  , где , где  ; ;
3)  , где , где  , ,
то процесс Зейделя сходится к единственному решению системы при любом выборе начального вектора.
Запишем систему (4.8) в сокращенном виде:
 (4.9) (4.9)
Введем обозначения:
 , ,
где
 , ,  . .
Тогда формулу (4.9) можем переписать в матричном виде:
 , (4.10) , (4.10)
где
 , ,  , ,  . .
Теорема 4.4 ( необходимые и достаточные условия сходимости метода Зейделя).
Для сходимости процесса Зейделя, заданного формулой (4.9), для приведенной системы линейных уравнений (4.4) при любом выборе свободного члена  и начального вектора и начального вектора  необходимо и достаточно, чтобы все корни необходимо и достаточно, чтобы все корни  уравнения уравнения  были по модулю меньше единицы. были по модулю меньше единицы.
3. Метод релаксации
Рассмотрим систему линейных алгебраических уравнений (4.1), в которой  . .
Сделаем преобразования: для этого свободные члены перенесем в левую часть и каждое  -тое уравнение поделим на -тое уравнение поделим на 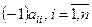 . Таким образом, получим систему, удобную для релаксации: . Таким образом, получим систему, удобную для релаксации:
 (4.12) (4.12)
где  . .
Введем понятие невязки для приближенного решения  . .
Пусть дана система  , тогда точное решение , тогда точное решение 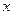 можно записать в виде можно записать в виде  , где , где  -правка корня -правка корня  . Подставим . Подставим  в систему, получим в систему, получим
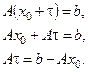
Введем обозначение  . Тогда . Тогда  . Выражение . Выражение  называется невязкой для приближенного решения называется невязкой для приближенного решения  . .
Пусть задано начальное приближение системы (4.12):
 . .
Подставим данное приближение в систему (4.12) и получим невязки 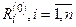 : :
 (4.13) (4.13)
Если одной из неизвестных  дать приращение дать приращение  , то соответствующая невязка , то соответствующая невязка  уменьшится на величину уменьшится на величину  , а все остальные невязки , а все остальные невязки  изменятся на величину изменятся на величину  . Чтобы обратить очередную невязку . Чтобы обратить очередную невязку  в нуль, нужно величине в нуль, нужно величине  дать приращение дать приращение  , следовательно, , следовательно,  , а остальные невязки будут равны , а остальные невязки будут равны
 . .
Метод релаксации (метод ослабления) заключается в том, что на каждом шаге обращают в нуль максимальную по модулю невязку путем изменения значения соответствующей компоненты приближения. Процесс заканчивается, когда все невязки последней преобразованной системы будут равны нулю с заданной точностью.
|