
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные типы уравнений с частными производными второго порядка. Начальные и краевые условия. Задача КошиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнение, связывающее неизвестную функцию нескольких переменных, ее частные производные и независимые переменные, называется уравнением в частных производных. Как и в случае обыкновенных дифференциальных уравнений, порядок уравнения определяется порядком старшей частной производной. Уравнение линейное, если оно первой степени относительно искомой функции и ее частных производных, и квазилинейное, если оно первой степени относительно старших производных. Чтобы составить себе представление о характере общего решения уравнения в частных производных, рассмотрим примеры. Пример. Найти общее решение уравнения ◄ Это уравнение 1-го порядка не содержит частной производной Пример. Найти общее решение уравнения ◄ Перепишем уравнение в виде:
Общее решение (общий интеграл) дифференциального уравнения с частными производными содержит, как правило, произвольные функции. Выделение частных решений (частных интегралов) производится путем задания соответствующих дополнительных условий, т. е. условий, налагаемых на искомую функцию нескольких переменных и/или ее частные производные. Многие математические модели реальных физических, механических, технологических процессов включают дифференциальные уравнения с частными производными второго порядка, называемых уравнениями математической физики. Их вывод основывается на механических или физических законах. Квазилинейное уравнение второго порядка относительно функции
Методы решения таких уравнений и характер описываемых этими уравнениями процессов зависят от того, к какому типу они относятся. Уравнение (5.25) является в точке · эллиптическим, если · гиперболическим,если · параболическим, если в точке
Пример. Определить тип уравнения ◄ В данном уравнении
Основными уравнениями математической физики являются следующие дифференциальные уравнения с частными производными второго порядка (для случая функций двух независимых переменных): 1. Волновое уравнение (одномерное):
К такому уравнению приводит рассмотрение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводе, колебаний газа, крутильных колебаний вала и т. д. в отсутствии внешних сил. Это уравнение является простейшим уравнением гиперболического типа. 2. Уравнение теплопроводности (одномерное):
К такому уравнению приводит рассмотрение процессов распространения тепла в теле без источников тепла, фильтрации нефти и газа в пористой среде, диффузии частиц в среде и т. д. Это уравнение является простейшим уравнением параболического типа. 3. Уравнение Лапласа (двумерное):
К такому уравнению приводит рассмотрение некоторых стационарных процессов в задачах электромагнетизма, о тепловом состоянии, диффузии, гидродинамики и т. д. Это уравнение является простейшим уравнением эллиптического типа. В трехмерном случае уравнение Лапласа принимает вид:
где Как видно из приведенных выше примеров, решение уравнения в частных производных зависит, вообще говоря, от произвольных функций. При этом одно и то же уравнение может описывать совершенно различные процессы или состояния. Для однозначного описания определенного процесса или состояния каждая задача математической физики ставится как задача решения некоторого уравнения при определенных дополнительных условиях, которые в большинстве случаев диктуются ее физической постановкой. Так, например, для однозначного описания колебаний струны или стержня необходимо дополнительно задать смещение
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1017; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.15.34 (0.007 с.) |

 .
.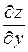 искомой функции двух переменных
искомой функции двух переменных  . Поэтому можно, фиксируя
. Поэтому можно, фиксируя  , рассматривать его как обыкновенное дифференциальное уравнение:
, рассматривать его как обыкновенное дифференциальное уравнение:  , где
, где 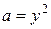 – постоянная величина. Последнее уравнение является уравнением с разделяющимися переменными
– постоянная величина. Последнее уравнение является уравнением с разделяющимися переменными  и
и  . Решаем его:
. Решаем его: 
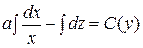 (вместо произвольной постоянной
(вместо произвольной постоянной  появляется произвольная функция
появляется произвольная функция  , частная производная которой по аргументу
, частная производная которой по аргументу 

 – общее решение заданного уравнения. ►
– общее решение заданного уравнения. ► .
. . Учитывая, что частная производная по
. Учитывая, что частная производная по  , где
, где  , где
, где 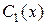 и
и  – произвольные функции переменных
– произвольные функции переменных 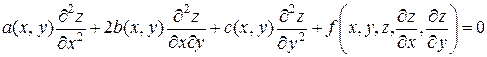 . (5.25)
. (5.25) (в некоторой области
(в некоторой области  ):
): ,
, ,
,
 (соответственно во все точках области
(соответственно во все точках области  .
. ,
, 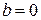 ,
, 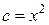 . Так как
. Так как  во всех точках, не лежащих на прямых
во всех точках, не лежащих на прямых  и
и  , то в любом открытом квадранте заданное уравнение имеет эллиптический тип. ►
, то в любом открытом квадранте заданное уравнение имеет эллиптический тип. ► (
( – время). (5.26)
– время). (5.26) . (5.27)
. (5.27)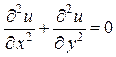 . (5.28)
. (5.28)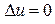 , (5.29)
, (5.29)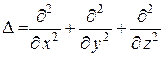 – оператор Лапласа.
– оператор Лапласа. и скорость
и скорость  в каждой точке струны в начальный момент времени
в каждой точке струны в начальный момент времени 


