
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции, отображения, отношенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные понятия Пусть даны два множества Например, соответствие между элементами множеств Пусть задано соответствие R и Y = R (Х). Ему соответствует точка M с координатами (х; у). Тогда множество точек плоскости, выделяемое отображением R, будет графиком. Задание отображений Для описания соответствий между множествами используют понятие отображения (функции) одного множества на другое. Для задания отображения необходимо указать: множество, которое отображается (область определения данного отображения, часто обозначается множество, в (на) которое отображается данная область определения (множество значений этого отображения, часто обозначается закон или соответствие между этими множествами, по которому для элементов первого множества (прообразов, аргументов) выбраны элементы (образы) из второго множества. Приняты записи Везде при записи Отображения задаются аналитически, таблично, графически. Способ задания отображения в виде формул называется аналитическим. Для задания отображения множеств табличным способом принято строить таблицу, в которой первую строку составляют элементы области определения (прообразы вида a), а вторую строку – их образы f (a). Графическое представление отображения связано со стрелочными схемами (диаграммами или графами), которые подробно рассматриваются в главе 2. Понятие «функция» является одним из основных в математике. В данном случае подразумевается прежде всего функция, отображающая одно конечное множество объектов в другое конечное множество. Поэтому по смыслу термин «отображение» и «функция» почти идентичны.
Виды отображений Различают два основных вида однозначных отображений (функций). По мощности они делятся на сюръективные и инъективные. Сюръекция – соответствие, при котором каждому элементу множества А указан единственный элемент множества В, а каждому элементу множества В можно указать хотя бы один элемент множества А, называется отображением множества А на множество В. Инъекция – соответствие, при котором каждому элементу множества А соответствует единственный элемент множества В, а каждому элементу В соответствует не более одного прообраза из А, называется отображением множества А во множество В. Биекцией называется отображение множества А на множество В, при котором каждому элементу множества В соответствует единственный элемент множества А, является взаимно-однозначным соответствием между двумя множествами. На рис. 1.10 изображены отображения Пусть множество А отображается взаимно-однозначнона множество В, т.е
Отношения Пусть А и В – два множества. Бинарным отношением R из множества А в множество В называется подмножество прямого (декартова) произведения А и В:
Если А = В, то R есть отношение на множестве А. Отношения являются частным случаем отображения, когда область определения и множество значений совпадают, поэтому всё сказанное в п. 1.4 справедливо и для отношений. Назовём n – местным отношением R на непустом множестве М, это подмножество Если отношение n – местное, то в общем случае можно записать
Множества Аi не обязательно различны, а отношение R – это множество упорядоченных кортежей Обратное отношение: Дополнение отношение Тождественное отношение: Композицией отношений R 1 и R 2 называется отношение, если
Свойства отношений Приведем характерные свойства бинарных отношений, причём заметим, что каждое конкретное отношение может обладать или не обладать некоторыми из указанных свойств. 1. Рефлексивность: 2. Антирефлексивность. Имеет место, когда отношение не обладает свойством 1 для любых а, например «быть больше», «быть младше» и др. 3. Симметричность любых двух элементов. Отношение R на множестве М называется симметричным, если для любых a, 4. Антисимметричность. Если для несовпадающих элементов а ≠ b верно отношение 5. Транзитивность. Если aRb и 6. Антитранзитивность. Имеет место, когда отношение не обладает свойством 5. Например, «быть перпендикулярным» на множестве прямых плоскости ( 7. Асимметричность. Ни для одной пары а и b не выполняется одновременно 8. Связность. Для любых а и b, если а ≠ b, то 9. Отношения эквивалентности Различные отношения могут обладать (или не обладать) теми или иными свойствами, приведенными выше. Некоторые устойчивые комбинации этих свойств встречаются настолько часто, что их следует выделить отдельно. Классы отношений, обладающие определённым набором свойств можно изучить отдельно. К таким классам отношений относятся: отношения эквивалентности, толерантности, порядка. Таблица Свойства бинарных отношений
Рассмотрим основные виды бинарных отношений. Отношение эквивалентности. Бинарное отношение R называется отношением эквивалентности, если оно одновременно обладает тремя свойствами: рефлексивностью, симметричностью и транзитивностью, т.е. если для любых x, y, z выполняется: xRx (рефлексивность); если xRy, то yRx (симметричность); если xRy, а yRz, то xRz (транзитивность). Обозначение эквивалентных отношений: а Q b или Непересекающиеся подмножества, на которые разбивается множество М отношением эквивалентности, называются классами эквивалентности. Множество классов эквивалентности множества А относительно Q называется фактор-множеством и обозначается Например, множество всех рациональных чисел Q можно разбить на классы эквивалентности, для которых а / b – рациональная дробь, где Рефлексивность. Для любой дроби а / b выполняется равенство ab=ba, значит а / b Q а / b. Симметричность. Если а / b Q c/d, то ad=bc, но bc = ad, значит c/d Q а / b. Симметричность равенства произведений влечёт за собой симметричность отношений между дробями. Транзитивность. Известно, что а / b Q c/d, c/d Q m/n. Докажем, что а / b Q m/n, т.е an=bm. Действительно, так как а / b Q c/d, то ad=bc, аналогично c/d Q m/n, то cn=md. Умножим первое равенство на n, а второе на b, тогда имеем adn=bcn и bcn=mdb. По свойству транзитивности
Отношения толерантности Отношение A на множестве M называется отношением толерантности, если оно рефлексивно и симметрично. Очевидно, что отношение эквивалентности есть частный случай толерантности, когда к двум перечисленным свойствам добавляется транзитивность. Например, отношение «быть другом» рефлексивно, симметрично, но не транзитивно. Таким образом, толерантность является более слабой мерой сходства, чем эквивалентность, но тем не менее помогает выявлять различия в схожих вещах. Пусть A и B имеют некоторые сходные признаки. Тогда A рефлексивно В (признаки не только схожи, но и совпадают). Очевидно, что выполняется и симметричность, т.е. порядок рассмотрения сходных объектов не важен. Однако накопление несущественных различий у некогда сходных объектов может впоследствии привести к их полному различию. Сложно разбить на классы множество, состоящее из сходных элементов, так как размыты границы признаков, по которым они объединяются в подмножества. Как известно, каждый элемент множества несёт определённую информацию обо всех его элементах. В случае отношения эквивалентности такая информация об одном элементе достаточно полно характеризует свойства всего множества, а отношение сходства малоинформативно. Тогда предельным случаем сходства является неразличимость (но не одинаковость). При изучении отношения сходства сначала определяется мера сходства – критерии, а затем исследуется взаимное расположение сходных объектов. Отношение толерантности даёт интуитивное представление о сходстве объектов. Понятно, что для толерантности свойство транзитивности излишне: сходство между парами a 1 и a 2, a 3 и a 4, …, an –1 и an не означает, что сходны между собой a 1 и an, так как размыты критерии сходства, и для каждой пары они могут быть разными. Например, вспомните эффект детской игры в «испорченный телефон». Пусть
Отношения порядка Отношение R называется отношением порядка на множестве M, если оно обладает свойствами антисимметричности и транзитивности. Для произвольного отношения порядка принято обозначение Множество M, которое обладает отношением порядка, называется упорядоченным. Такое определение не противоречит определению конечного упорядоченного множества, a является его обобщением на бесконечные множества. И наоборот, старое определение является частным случаем этого, так как сравнение на множестве происходит за счёт естественного упорядочения натуральных чисел, заложенного в определении N. Упорядочено множество цифр в моем телефонном номере и множество букв в вашем имени. Отношение порядка может быть рефлексивным и тогда оно называется отношением нестрогого порядка и обозначается знаком Отношение нестрогого порядка должно удовлетворять трём условиям: рефлексивности, т.е. xRx; антисимметричности, т.е. если xRy и yRx, то x=y; транзитивности, т.е. если xRy, а yRz, то xRz. Отношение нестрогого порядка является объединением отношения строгого порядка и отношения тождественности. Каждому отношению порядка R на множестве M можно поставить в соответствие обратное отношение порядка Отношение порядка даёт возможность сравнивать между собой различные элементы множества M. Пусть M – упорядоченное множество с отношением строгого порядка
На множестве N натуральных чисел выполняются лишь свойства антисимметричности и транзитивности. Поэтому на нём установлено отношение полного порядка: для любой пары натуральных чисел единица является предшествующим числом, т.е. минимальным. Можно доказать, что конечное вполне упорядоченное множество содержит единственный минимальный элемент. Например, на множествах чисел Всякий частичный порядок на конечном множестве может быть доведён до полного. То есть существует такое отношение полного порядка, для которого заданное отношение частичного порядка является подмножеством.
Тема 18 Графы
Лекция 18.1 «Графы» Учебные вопросы: 1. Основные характеристики графов 2. Матричные способы задания графов 3. Изоморфизм графов
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 2975; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.241.235 (0.009 с.) |

 и
и  . Тогда пары (ai, bi) задают соответствие между множествами А и В, если указано правило R, по которому для элемента ai множества А выбирается элемент bi из множества В.
. Тогда пары (ai, bi) задают соответствие между множествами А и В, если указано правило R, по которому для элемента ai множества А выбирается элемент bi из множества В. и
и  задаёт точечное множество (хi; уi) координат точек на плоскости.
задаёт точечное множество (хi; уi) координат точек на плоскости.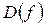 );
); );
); или
или  .
. . Далее будем иметь дело в основном с однозначными отображениями, где каждому аргументу поставлено в соответствие не более одного образа.
. Далее будем иметь дело в основном с однозначными отображениями, где каждому аргументу поставлено в соответствие не более одного образа. .
. . Так как одному образу при биекции соответствует в точности один прообраз, обратное отображение будет определено всюду на В и однозначно.
. Так как одному образу при биекции соответствует в точности один прообраз, обратное отображение будет определено всюду на В и однозначно.
 . Для бинарных отношений используется следующая форма записи:
. Для бинарных отношений используется следующая форма записи: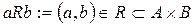 .
. . При
. При  отношение R называется бинарным. То есть бинарным отношением между элементами множеств А и В называют любое подмножество R множества А×В.
отношение R называется бинарным. То есть бинарным отношением между элементами множеств А и В называют любое подмножество R множества А×В. .
. .
. .
. .
. .
. ,
,  ,
,  .
. , например, «быть не больше» на R.
, например, «быть не больше» на R. одновременно справедливо
одновременно справедливо  и
и  (т.е.
(т.е.  ). Симметрична параллельность прямых, так как если а || b, то b || а. Симметрично отношение «быть равным» на любом множестве или «быть взаимно простым» на N.
). Симметрична параллельность прямых, так как если а || b, то b || а. Симметрично отношение «быть равным» на любом множестве или «быть взаимно простым» на N. , то ложно
, то ложно  . Антисимметричными являются отношения «быть больше», «не меньше» на R, «быть делителем» на N и др.
. Антисимметричными являются отношения «быть больше», «не меньше» на R, «быть делителем» на N и др. , то aRc для любых
, то aRc для любых  . Транзитивны отношения «быть больше», «быть параллельным», «быть равным» и др.
. Транзитивны отношения «быть больше», «быть параллельным», «быть равным» и др. , но неверно
, но неверно  ).
).


 , что означает «а эквивалентно b в отношении Q», например, «быть равным на множестве чисел», «быть подобным на множестве геометрических фигур».
, что означает «а эквивалентно b в отношении Q», например, «быть равным на множестве чисел», «быть подобным на множестве геометрических фигур». .
.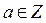 ;
;  . Любая дробь c / b будет отнесена к тому же классу тогда и только тогда, когда ad=bc, т.е а / b и Q эквивалентны, если ad=bc (например, –2/4 ~ –3/6). Проверим выполнимость свойств для такого решения.
. Любая дробь c / b будет отнесена к тому же классу тогда и только тогда, когда ad=bc, т.е а / b и Q эквивалентны, если ad=bc (например, –2/4 ~ –3/6). Проверим выполнимость свойств для такого решения. или
или  . Известно, что такие дроби классифицируется по элементу, порождающему класс эквивалентности, которым в этом примере является несократимая дробь (например, для 2/4~3/6~4/8 таковой будет 1/2).
. Известно, что такие дроби классифицируется по элементу, порождающему класс эквивалентности, которым в этом примере является несократимая дробь (например, для 2/4~3/6~4/8 таковой будет 1/2). . Обозначим через
. Обозначим через  совокупность всех непустых подмножеств множества
совокупность всех непустых подмножеств множества  . Два таких подмножества будут толерантными, если у них есть хотя бы один общий элемент.
. Два таких подмножества будут толерантными, если у них есть хотя бы один общий элемент. , означающее предшествование.
, означающее предшествование. . Если отношение порядка антирефлексивно, то оно называется отношением строгого порядка и обозначается
. Если отношение порядка антирефлексивно, то оно называется отношением строгого порядка и обозначается  . Отношение полного порядка, если сравнимы все элементы множества.
. Отношение полного порядка, если сравнимы все элементы множества. . Например, отношения «больше» и «меньше» на множестве действительных чисел. Для связного отношения порядка R на множестве M существует ему противоположное
. Например, отношения «больше» и «меньше» на множестве действительных чисел. Для связного отношения порядка R на множестве M существует ему противоположное  , причём, если R – отношение нестрогого порядка, то
, причём, если R – отношение нестрогого порядка, то  .
. говорят, что элемент x предшествует элементу y. Пусть M – вполне упорядоченное множество. Тогда, если для элемента x не нашлось предшествующего, то он называется минимальным, т.е. не существует элементов y, «меньших», чем x. Символически это записывается так:
говорят, что элемент x предшествует элементу y. Пусть M – вполне упорядоченное множество. Тогда, если для элемента x не нашлось предшествующего, то он называется минимальным, т.е. не существует элементов y, «меньших», чем x. Символически это записывается так:

 и
и  .
.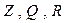 отношения
отношения  и
и  есть отношения нестрогого полного порядка, а отношения < и > есть отношения строгого полного порядка. Отношение Ì есть отношение нестрогого частичного порядка на множестве
есть отношения нестрогого полного порядка, а отношения < и > есть отношения строгого полного порядка. Отношение Ì есть отношение нестрогого частичного порядка на множестве 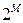 (булеан).
(булеан).


