
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 24 Приближенное решение дифференциальных уравнений и системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Лекция 24.1 «Приближенное решение дифференциальных уравнений и систем» Учебные вопросы: 1. Метод Эйлера 2. Метод Рунге-Кутта 3. Метод Адамса
Дифференциальные уравнения являются основным математическим инструментом моделирования и анализа разнообразных явлений и процессов в науке и технике. Методы их решения подразделяются на два класса: 1) аналитические методы, в которых решение получается в виде аналитических функций; 2) численные (приближенные) методы, где искомые интегральные кривые получают в виде таблиц их численных значений. Применение аналитических методов позволяет исследовать полученные решения методами математического анализа и сделать соответствующие выводы о свойствах моделируемого явления или процесса. К сожалению, с помощью таких методов можно решать достаточно ограниченный круг реальных задач. Численные методы позволяют получить с определенной точностью приближенное решение практически любой задачи. Решить дифференциальное уравнение
численным методом означает, что для заданной последовательности аргументов
Рассмотрим три наиболее распространенных при решении практических задач численных метода интегрирования Эйлера, Рунге-Кутта и Адамса. Метод Эйлера. Этот метод является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других численных методов. Пусть дано дифференциальное уравнение с начальными условиями (задача Коши)
и выполняются условия существования и единственности решения. Теорема Пиккара (теорема о существовании и единственности решения задачи Коши). Если в уравнении (7.1) функция
где Требуется найти решение Выбрав шаг
Искомую интегральную кривую  , проходящую через точку , проходящую через точку  , приближенно заменим ломаной Эйлера с вершинами , приближенно заменим ломаной Эйлера с вершинами 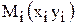 (Рис.7.1). (Рис.7.1).Звено ломаной
Сделав преобразование, получим формулу Эйлера:
Вычисление значений
Далее определяя значение аргумента
Поступая аналогичным образом при Таким образом, соединяя на координатной плоскости точки Метод Эйлера может быть применен к решению систем дифференциальных уравнений. Пусть задана система двух уравнений первого порядка
с начальными условиями
Необходимо найти решение этой задачи Коши. Проводя аналогичные рассуждения, получаем расчетные формулы вида:
где При расчетах полагается, что Запишем разложение
Учитывая формулы (7.3) и (7.8), получим
Соотношение (7.9) может быть использовано для выбора шага Достоинством метода Эйлера является его простота и высокая скорость поиска решения. Недостатком метода Эйлера является малая точность.
Метод Рунге-Кутта Данный метод является одним из наиболее распространенных численных методов интегрирования обыкновенных дифференциальных уравнений. По сравнению с описанным выше методом Эйлера метод Рунге-Кутта имеет более высокую точность, но невысокую скорость поиска решения, так как метод относится к классу многошаговых методов. Пусть на отрезке Выражение (7.2) можно переписать в виде:
где Придадим аргументу
Перенося первое слагаемое в этой сумме в левую часть получим, что
Здесь производные Вместо непосредственных вычислений по формуле (7.3) в методе Рунге-Кутта для каждого значения
Если числа
Формула Рунге-Кутта имеет погрешность Таким образом, рабочая формула Рунге-Кутта:
В отличие от расчетной схемы метода Эйлера, в которой каждое следующее значение Метод Рунге-Кутта может быть использован и при решении систем дифференциальных уравнений. Рассмотрим задачу Коши для системы второго порядка (7.6). В этом случае приращения
где
Приближенное интегрирование системы уравнений (7.6) осуществляется по формулам вида:
Метод Адамса Пусть для задачи Коши найдены каким-либо способом (например, методом Эйлера или Рунге-Кутта) три последовательных значения искомой функции
Вычислим величины Метод Адамса позволяет найти решение задачи – функцию
Затем уточнение проводится по интерполяционной формуле Адамса:
Метод Адамса легко распространяется на системы дифференциальных уравнений. Погрешность метода Адамса имеет тот же порядок, что и метод Рунге-Кутта. Тема 25 Основные понятия теории вероятностей
Лекция 25.1 «Основные понятия теории вероятностей. Формулы комбинаторики» Учебные вопросы: 1. Случайные события. Алгебра случайных событий 2. Вероятность. Дискретное и непрерывное вероятностные пространства 3. Комбинаторный метод вычисления вероятностей в классической схеме
|
|||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 559; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.13.119 (0.007 с.) |

 (7.1)
(7.1) и числа
и числа  , не определяя аналитического вида функции
, не определяя аналитического вида функции 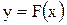 , найти значения
, найти значения  , удовлетворяющие условиям:
, удовлетворяющие условиям: .
. (7.2)
(7.2) непрерывна в прямоугольнике
непрерывна в прямоугольнике  и удовлетворяет в
и удовлетворяет в  условию Липшица
условию Липшица ,
, - константа Липшица, то существует единственное решение
- константа Липшица, то существует единственное решение 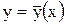 ,
,  , уравнения (7.1), удовлетворяющее условию
, уравнения (7.1), удовлетворяющее условию  , где
, где 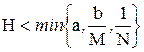 ,
,  в
в  задачи Коши (7.2) на отрезке
задачи Коши (7.2) на отрезке  .
. - достаточно малый, равный
- достаточно малый, равный  , строим систему равноотстоящих точек
, строим систему равноотстоящих точек 

 , заключенное между
, заключенное между  и
и  , наклонено к оси
, наклонено к оси  под углом
под углом  . Тангенс этого угла вычисляется по формуле:
. Тангенс этого угла вычисляется по формуле: .
. . (7.3)
. (7.3) осуществляется с использованием формулы (7.3) следующим образом. По заданным начальным условиям
осуществляется с использованием формулы (7.3) следующим образом. По заданным начальным условиям  и
и  полагая
полагая  в выражении (7.3) вычисляется значение
в выражении (7.3) вычисляется значение (7.4)
(7.4) по формуле
по формуле  , используя найденное значение
, используя найденное значение 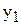 и полагая в формуле (7.3)
и полагая в формуле (7.3)  вычисляем следующее приближенное значение интегральной кривой
вычисляем следующее приближенное значение интегральной кривой  , как
, как (7.5)
(7.5) определяем все остальные значения
определяем все остальные значения 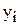 , в том числе последнее значение
, в том числе последнее значение  , которое соответствует значению аргумента
, которое соответствует значению аргумента  .
.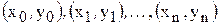 отрезками прямых в качестве приближенного представления искомой интегральной кривой
отрезками прямых в качестве приближенного представления искомой интегральной кривой  .
.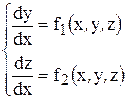 (7.6)
(7.6) .
. (7.7)
(7.7)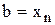 . В результате применения расчетной схемы (7.7) получается приближенное представление интегральных кривых
. В результате применения расчетной схемы (7.7) получается приближенное представление интегральных кривых  и
и  в форме двух ломаных Эйлера, построенных по полученным таблицам
в форме двух ломаных Эйлера, построенных по полученным таблицам  .
. в ряд Тейлора:
в ряд Тейлора: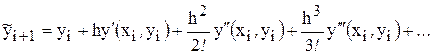 (7.8)
(7.8) (7.9)
(7.9)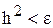 , где
, где  - заданная точность.
- заданная точность. требуется найти численное решение задачи Коши (7.1), где
требуется найти численное решение задачи Коши (7.1), где  равных частей и построим последовательность значений
равных частей и построим последовательность значений  аргумента
аргумента  (7.10)
(7.10) - приращение искомой функции
- приращение искомой функции  -ом шаге интегрирования.
-ом шаге интегрирования. в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 
 (7.11)
(7.11) определяются последовательным дифференцированием уравнения (7.1).
определяются последовательным дифференцированием уравнения (7.1). определяются четыре числа:
определяются четыре числа: (7.12)
(7.12)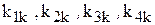 последовательно умножить на
последовательно умножить на  и сложить между собой, то получим:
и сложить между собой, то получим: . (7.13)
. (7.13) .
. .
. вычисляется непосредственно по единой формуле (7.3), в методе Рунге-Кутта необходимо проведение промежуточных вычислений по формулам (7.10) и (7.12).
вычисляется непосредственно по единой формуле (7.3), в методе Рунге-Кутта необходимо проведение промежуточных вычислений по формулам (7.10) и (7.12). вычисляются по формулам:
вычисляются по формулам: (7.14)
(7.14)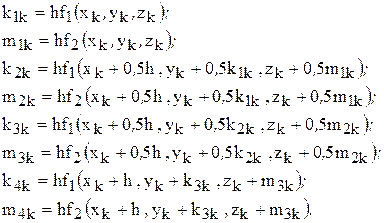 (7.15)
(7.15) .
.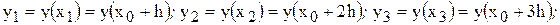
 ,
,  ,
,  ,
,  .
.
 .
.


