Ряд Тейлора. Разложение функций в степенные ряды
Похожие статьи вашей тематики
Для функции  , имеющей все производные до , имеющей все производные до  -го порядка включительно, в окрестности точки -го порядка включительно, в окрестности точки  (т. е на некотором интервале, содержащем точку (т. е на некотором интервале, содержащем точку  ) справедлива формула Тейлора: ) справедлива формула Тейлора:

 , (3.18) , (3.18)
где  – так называемый остаточный член. – так называемый остаточный член.
Если функция  имеет производные всех порядков в окрестности точки имеет производные всех порядков в окрестности точки  и и  в этой окрестности, то справа в формуле получается степенной ряд, который называется рядом Тейлора: в этой окрестности, то справа в формуле получается степенной ряд, который называется рядом Тейлора:

 (3.19) (3.19)
Последнее равенство справедливо лишь в том случае, если 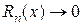 при при 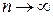 . В этом случае степенной ряд справа сходится и его сумма равна данной функции . В этом случае степенной ряд справа сходится и его сумма равна данной функции  (говорят, что функция (говорят, что функция  разложена в ряд по степеням разложена в ряд по степеням 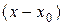 ). Если же ). Если же  , то ряд не представляет данной функции, хотя может и сходиться (к другой функции). , то ряд не представляет данной функции, хотя может и сходиться (к другой функции).
Частный случай ряда Тейлора при  иногда называют рядом Маклорена. Он имеет вид иногда называют рядом Маклорена. Он имеет вид
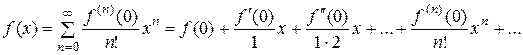 (3.20) (3.20)
Для каждой из элементарных функций существует такое 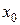 и и  , что в интервале , что в интервале  она разлагается в ряд Тейлора или (если она разлагается в ряд Тейлора или (если  ) в ряд Маклорена. ) в ряд Маклорена.
Разложение некоторых элементарных функций в ряд Маклорена:
·  , ,  ; (3.21) ; (3.21)
·  , ,  ; (3.22) ; (3.22)
·  , ,  ; (3.23) ; (3.23)
·  , ,  ; (3.24) ; (3.24)
· Биномиальный ряд
 , (3.25) , (3.25)
где  – произвольное постоянное число, – произвольное постоянное число,  . .
Пример. Разложить  в ряд Тейлора по степеням в ряд Тейлора по степеням  . .
◄ Имеем:  ; ;
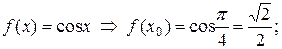




…
Таким образом,

 . ► . ►
Ряды Фурье
Функциональный ряд вида
 , (3.26) , (3.26)
называется тригонометрическим рядом. Постоянные числа  и и  ( ( =1, 2, …) называются коэффициентами тригонометрического ряда. =1, 2, …) называются коэффициентами тригонометрического ряда.
Если ряд (3,26) сходится, то его сумма есть периодическая функция  с периодом с периодом  , т. е. , т. е. 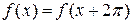 , так как , так как  и и  являются периодическими функциями с периодом являются периодическими функциями с периодом  . .
Рядом Фурье интегрируемой и периодической с периодом  интегрируемой функции интегрируемой функции  называется тригонометрический ряд (3.26) с коэффициентами называется тригонометрический ряд (3.26) с коэффициентами  и и  ( ( =1, 2, …), определяемыми формулами: =1, 2, …), определяемыми формулами:
 (свободный член), (3.27) (свободный член), (3.27)
 , ( , ( =1, 2, …), (3.28) =1, 2, …), (3.28)
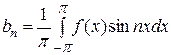 , ( , ( =1, 2, …). (3.29) =1, 2, …). (3.29)
Определенные по формулам (3.27) ― (3.29) коэффициенты называются коэффициентами Фурье функции  . Теория разложения функций в ряды Фурье называется гармоническим анализом. . Теория разложения функций в ряды Фурье называется гармоническим анализом.
Ряд Фурье функции  может либо расходиться, либо сходиться, причем как к функции может либо расходиться, либо сходиться, причем как к функции  , так и к функции, отличной от нее. Условия сходимости ряда Фурье даются теоремой Дирихле. , так и к функции, отличной от нее. Условия сходимости ряда Фурье даются теоремой Дирихле.
Теорема Дирихле. Если функция  непрерывна или имеет конечное число точек разрыва на отрезке непрерывна или имеет конечное число точек разрыва на отрезке  и при этом монотонна или имеет конечное число экстремумов на и при этом монотонна или имеет конечное число экстремумов на  , то ряд Фурье функции , то ряд Фурье функции  сходится для любых сходится для любых  из из  и его сумма равна: и его сумма равна:
1)  для всех точек непрерывности для всех точек непрерывности  из интервала из интервала  ; ;
2)  для всех точек разрыва для всех точек разрыва 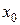 , где , где 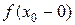 и и  – левосторонний и правосторонний предел функции в этих точках, соответственно; – левосторонний и правосторонний предел функции в этих точках, соответственно;
3) 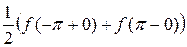 при при  и и  . .
Пример. Разложить в ряд Фурье периодическую функцию  с периодом с периодом  , определенную следующим образом: , определенную следующим образом:  . .

Рис. 1
◄ Эта функция кусочно монотонная и ограниченная. Следовательно, она допускает разложение в ряд Фурье. Вычисляем коэффициенты Фурье:


= 

= 
Окончательно получаем
 . .
В точках разрыва функции  сумма ряда равна среднему арифметическому ее пределов справа и слева, т. е. в данном случае сумма ряда равна среднему арифметическому ее пределов справа и слева, т. е. в данном случае 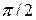 . ► . ►
Если  является четной функцией является четной функцией  , то , то  =0 ( =0 ( =1, 2, …) и, следовательно, разложение четной функции в ряд Фурье будет содержать только косинусы: =1, 2, …) и, следовательно, разложение четной функции в ряд Фурье будет содержать только косинусы:
 , ,
где
 , , 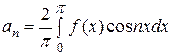 , ( , ( =1, 2, …). (3.30) =1, 2, …). (3.30)
Для нечетной функции   коэффициенты коэффициенты 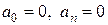 ( ( =1, 2, …) и, следовательно, ряд Фурье для нечетной функции будет содержать только синусы: =1, 2, …) и, следовательно, ряд Фурье для нечетной функции будет содержать только синусы:
 , ,
где
 , ( , ( =1, 2, …). (3.31) =1, 2, …). (3.31)
Эти формулы позволяют упрощать вычисления при нахождении коэффициентов Фурье в тех случаях, когда заданная функция является четной или нечетной. Но следует отметить, что не всякая периодическая функция является четной или нечетной.
Пример. Разложить в ряд Фурье периодическую функцию  с периодом с периодом  , определенную следующим образом: , определенную следующим образом:  (рис. 2). (рис. 2).
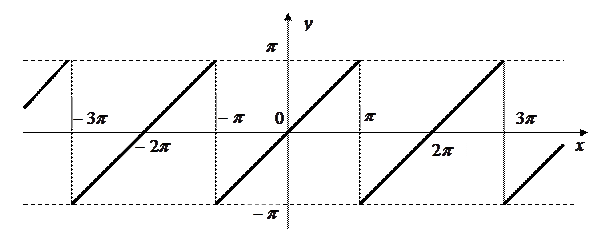
Рис. 2
◄ Заданная функция является нечетной. Следовательно, в ее разложении будут только синусы. По формуле (3.31) вычисляем коэффициенты 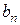 : :
 . .
Таким образом, получаем ряд
 . .
Это равенство имеет место во всех точках, кроме точек разрыва. В каждой точке разрыва сумма ряда равна среднему арифметическому ее пределов справа и слева, т. е. нулю. ►
|