Комплексные числа. Алгебра комплексных чисел
Комплексные числа не являются числами в элементарном смысле слова, применяемыми при подсчетах и измерениях. Они составляют новый класс абстрактных математических объектов, определяемый описанными ниже свойствами.
Каждому комплексному числу  можно поставить в соответствие единственную пару можно поставить в соответствие единственную пару  действительных чисел действительных чисел  и и  и обратно ( и обратно (  ). Действительные числа ). Действительные числа  содержатся в классе комплексных чисел в качестве пар содержатся в классе комплексных чисел в качестве пар  . Пары . Пары  называются чисто мнимыми комплексными числами. Комплексное число называются чисто мнимыми комплексными числами. Комплексное число  называется мнимой единицей. называется мнимой единицей.
Сумма и произведение двух комплексных чисел  и и  определяются соответственно следующим образом: определяются соответственно следующим образом:
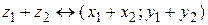 , (1.4.1) , (1.4.1)
 . (1.4.2) . (1.4.2)
Два комплексных числа  и и  равны ( равны (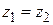 ) тогда и только тогда, когда ) тогда и только тогда, когда  и и  . .
Если  и и  действительны (т. е. действительны (т. е.  ), то определение (1.4.2) совпадает с обычным. При ), то определение (1.4.2) совпадает с обычным. При  = =  = =  из определения произведения следует: из определения произведения следует:
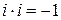 . (1.4.3) . (1.4.3)
Справедливы следующие законы сложения и умножения комплексных чисел:
a)  , ,  (переместительный); (переместительный);
b)  , ,  (сочетательный); (сочетательный);
c) 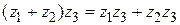 (распределительный (относительно сложения)). (распределительный (относительно сложения)).
Каждое комплексное число может быть записано в виде суммы  (алгебраическая форма комплексного числа) действительного числа (алгебраическая форма комплексного числа) действительного числа  и чисто мнимого числа и чисто мнимого числа 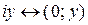 . Действительные числа . Действительные числа  и и  соответственно называются действительной и мнимой частью комплексного числа соответственно называются действительной и мнимой частью комплексного числа  . Два комплексных числа . Два комплексных числа  и и 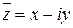 , имеющие одинаковые действительные и противоположные мнимые части, называются сопряженными комплексными числами. , имеющие одинаковые действительные и противоположные мнимые части, называются сопряженными комплексными числами.
При сложении комплексных чисел согласно (1.4.1) необходимо отдельно сложить их действительные и мнимые части. Сложение допускает обратную операцию: для любых двух комплексных чисел  и и 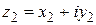 можно найти такое число можно найти такое число  , что , что  . Это число называется разностью чисел . Это число называется разностью чисел  и и  и обозначается символом и обозначается символом  . Очевидно, . Очевидно,
 . (1.4.4) . (1.4.4)
Перемножение двух комплексных чисел, записанных в алгебраической форме, будет согласовано с определением (1.4.2), если его производить по обычным правилам алгебры с заменой произведения  на на  . .
Пример. Даны три комплексных числа:  , ,  , ,  . Вычислить . Вычислить  . .
◄ 
 . ► . ►
Произведение комплексного числа  на сопряженное ему число на сопряженное ему число 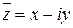 всегда неотрицательное действительное число. В самом деле, всегда неотрицательное действительное число. В самом деле,
 . (1.4.4) . (1.4.4)
Число  называется частным двух чисел называется частным двух чисел  и и  и обозначается символом и обозначается символом  , если , если 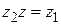 ( ( ). Деление комплексных чисел ). Деление комплексных чисел  проводится при использовании формулы проводится при использовании формулы
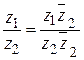 . (1.4.5) . (1.4.5)
Пример: 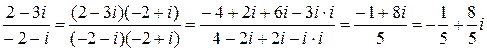 . .
Произведение  равных комплексных чисел равных комплексных чисел  называется называется  -й степенью числа -й степенью числа  и обозначается символом и обозначается символом  : :
 . .
Обратная операция – извлечение корня – определяется следующим образом: число  называется корнем называется корнем  -й степени из числа -й степени из числа  , если , если  (обозначается символом (обозначается символом  , причем для , причем для  пишут просто пишут просто  ). ).
Равенство (1.4.3) можно записать в виде  , и для мнимой единицы , и для мнимой единицы  имеем: имеем:
 . (1.4.6) . (1.4.6)
|