Итерационные методы решения систем нелинейных уравнений
Похожие статьи вашей тематики
Системами нелинейных уравнений (СНУ) называются системы вида:
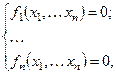 (3.1) (3.1)
если хотя бы одна из функций  нелинейна. Здесь нелинейна. Здесь 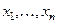 - неизвестные переменные. - неизвестные переменные.
Решение систем нелинейных уравнений – одна из трудных задач вычислительной математики. Трудность состоит в том, чтобы определить: имеет ли система решение, и, если – да, то сколько. Уточнение решений в заданной области – более простая задача.
Пусть функции  определены в областях определены в областях 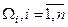 . Тогда область . Тогда область 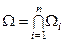 и будет той областью, где можно найти решение. и будет той областью, где можно найти решение.
Наиболее распространенными методами уточнения решения являются метод простых итераций, метод Ньютона и его модификация.
Метод простых итераций
Из исходной системы (3.1) путем эквивалентных преобразований переходим к системе вида:
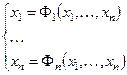 (3.2) (3.2)
Итерационный процесс, определяемый формулами
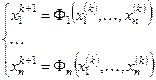 , , 
можно начать, задав начальное приближение  . Достаточными условиями сходимости итерационного процесса являются одно из двух следующих условий: . Достаточными условиями сходимости итерационного процесса являются одно из двух следующих условий:
 или или 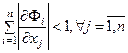 . .
Распишем первое условие:
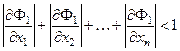 при при 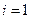 , ,
……………………………..
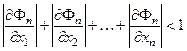 при при 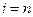 . .
Распишем второе условие:
 при при 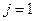 , ,
………………………………
 при при 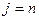 . .
Рассмотрим один из способов приведения системы (3.1) к виду (3.2), допускающему сходящиеся итерации.
Пусть задана система второго порядка вида:
 . .
Требуется привести ее к виду:
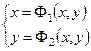 . .
Умножим первое уравнение системы на неизвестную постоянную  , второе - на , второе - на  , затем сложим их и добавим в обе части уравнения , затем сложим их и добавим в обе части уравнения 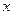 . Получим первое уравнение преобразованной системы . Получим первое уравнение преобразованной системы
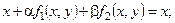
где 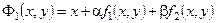 . .
Далее, умножим первое уравнение системы на неизвестную постоянную 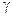 , второе - на , второе - на 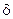 , затем сложим их и добавим в обе части уравнения , затем сложим их и добавим в обе части уравнения 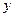 . Тогда второе уравнение преобразованной системы будет иметь вид . Тогда второе уравнение преобразованной системы будет иметь вид
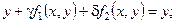
где  . .
Неизвестные постоянные 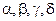 определим из достаточных условий сходимости определим из достаточных условий сходимости
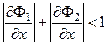 и и 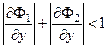 . (3.3) . (3.3)
Запишем эти условия более подробно:
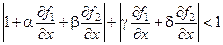
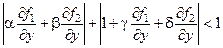
Полагая равными нулю выражения под знаком модуля, получим систему линейных алгебраических уравнений 4 порядка с четырьмя неизвестными для определения постоянных 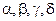 : :
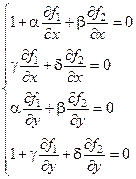 . (3.4) . (3.4)
При таком выборе параметров условия сходимости будут соблюдены, если частные производные функций 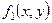 и и 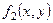 будут изменяться не очень быстро в окрестности точки будут изменяться не очень быстро в окрестности точки 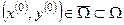 . Тогда, для того, чтобы решить систему (3.1), нужно задать начальное приближение . Тогда, для того, чтобы решить систему (3.1), нужно задать начальное приближение 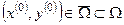 и вычислить значения производных и вычислить значения производных 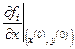 и и 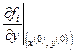 , , 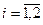 в этой точке. В противном случае, вычисление в этой точке. В противном случае, вычисление 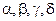 осуществляется на каждом осуществляется на каждом  шаге итераций, при этом шаге итераций, при этом 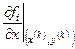 , , 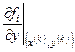 , , 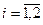 . .
Метод простых итераций является самоисправляющимся, универсальным и простым для реализации на ЭВМ. Если система имеет большой порядок, то применение данного метода, имеющего медленную скорость сходимости, не рекомендуется. В этом случае, используют метод Ньютона, который имеет более быструю сходимость.
|