Декартово произведение множеств

Пусть A – конечное множество, состоящее из n элементов. Кортежем длины n элементов множества A называется упорядоченная последовательность (а ₁, а ₂, …, а_n) элементов этого множества.

Кортежи (а ₁, а ₂, …, а_k) и (b ₁, b ₂, …, b_n) называются равными, если они имеют одинаковую длину и их элементы с одинаковыми номерами совпадают, т.е. (а ₁, а ₂, …, а_k) = (b ₁, b ₂, …, b_n), если (k=n) и для " i a_i = b_i.

Например, равны кортежи (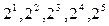) = , так как оба кортежа длины 5 и равны все пары соответствующих элементов данных множеств: , , , , .

Из двух данных кортежей (а ₁, а ₂, …, a_i, …, а_k), где , длины k и (b ₁, b ₂, …, b_j, …, b_m), где , длины m можно составить новый кортеж длиной , элементы которого (а ₁, а ₂, …, а_k, b ₁, b ₂, …, b_m) принадлежат множеству . Эта операция называется соединением кортежей. Кортеж можно образовать двумя способами, поэтому важно, какой кортеж назван первым. Так, соединив кортежи четных и нечетных однозначных чисел и , получим кортеж всех однозначных чисел .

Пусть A – конечное множество, элементами которого являются некоторые символы, например цифры, буквы, знаки препинания. Такие множества принято называть алфавитом над заданным множеством символов. Алфавит есть кортеж попарно различимых символов, называемых буквами алфавита. Элементы множества Aⁿ принято называть словами длины n в алфавите A. Слово над алфавитом есть просто некоторая конечная последовательность символов. Так, шестизначный телефонный номер является словом длины 6 над алфавитом цифр .

Рассмотрим множество B, состоящее из двух элементов: 0 и 1. Кортежи длины m из этих элементов обозначим B^m. Тогда . Такие кортежи называют упорядоченными наборами или векторами. Они имеют широкое применение в дискретной математике.

Вектор из нулей и единиц можно рассматривать как двоичное представление натурального числа.

Вектор, состоящий из единиц и нулей, описывает состояние памяти вычислительных машин, причём память может содержать числа, тексты, команды и т.д.

Пусть заданы множества . Декартовым произведением этих множеств называется множество , состоящее из всех кортежей длины n, в которых , где . Поскольку для задания кортежа важен порядок, то порядок множителей важен и в декартовом произведении.

Например, декартовым произведением множеств и будет являться множество пар . Скобки для указания пар опускают там, где это не может привести к затруднениям: . Если множества А:= и В:= конечны, то их декартово произведение может быть представлено в общем виде таблицей из m столбцов и k строк:

 

(a 1, b 1)	(a 1, b 2)	…	(a 1, bm)
(a 2, b 1)	(a 2, b 2)	…	(a 2, bm)
…	…	…	…
(ak, b 1)	(ak, b 2)	…	(ak, bm)

 

 

Если известны мощности множеств | А | и | В |, то | А × В |=| А | | В |.

Если А ₁ = А ₂=…= А_n = А, то пишут Аⁿ = А×A×…×A и называют n-й декартовой степенью множества A. Тогда можно записать | А | ⁿ =| Аⁿ |.

Например, плоскость является декартовым квадратом двух прямых и обозначается соответственно R ². В физике пространственно-временной континуум есть декартово произведение R ³ ×T, где R ³ – трехмерное пространство, а T – числовая ось времени.

Декартово произведение не обладает переместительным законом, т.е. вообще говоря, пары (a;b) и (b;a) различны: Х×Y≠ Y×Х. Так, различны точки плоскости с координатами (5;3) и (3;5). Но для произвольного и пустого множеств справедливо .

Свое название декартово произведение получило в честь выдающегося французского математика и философа Рене Декарта (1596–1650), являющегося автором знаменитого метода координат. На плоскости двумерные кортежи – это пара вида (х; у), а в пространстве – трехмерные кортежи в виде тройки чисел (х; у; z).