
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расширенное декартово произведениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кроме трех перечисленных операций в рамках реляционной алгебры определена еще одна теоретико-множественная операция — расширенное декартово произведение. Эта операция не накладывает никаких дополнительных условий на схемы исходных отношений, поэтому операция расширенного декартова произведения, обозначаемая Сцеплением, или конкатенацией, кортежей c = <c1, c2,..., cn> и q = <q1, q2,..., qm> называется кортеж, полученный добавлением значений второго в конец первого. Сцепление кортежей c и q обозначается как (c, q). (c, q) = <c1, c2,..., cn, q1, q2,..., qm> Здесь n — число элементов в первом кортеже с, m — число элементов во втором кортеже q. Все предыдущие операции не меняли степени или арности отношений — это следует из определения эквивалентности схем отношений. Операция декартова произведения меняет степень результирующего отношения. Расширенным декартовым произведением отношения R1 степени n со схемой SR1 = (A1, A2,..., An), и отношения R2 степени m со схемой SR2 = (B1, B2,..., Bm), называется отношение R3 степени n+m со схемой SR3 = (A1, A2,..., An, B1, B2,..., Bm), содержащее кортежи, полученные сцеплением каждого кортежа r отношения R1 с каждым кортежем q отношения R2. То есть если R1 = { r }, R2 = { q }
Операцию декартова произведения с учетом возможности перестановки атрибутов в отношении можно считать симметричной. Очень часто операция расширенного декартова произведения используется для получения некоторого универсума — т. е. отношения, которое характеризует все возможные комбинации между элементами отдельных множеств. Однако самостоятельного значения результат выполнения операции обычно не имеет, он участвует в дальнейшей обработке.
- Специальные операции (выбор, проекция, соединение, деление) Выбор (фильтрация) Первой специальной операцией реляционной алгебры является выбор (горизонтальный выбор, фильтрация, ограничение отношений). Для определения этой операции нам необходимо ввести дополнительные обозначения. Пусть а — булевское выражение, составленное из термов сравнения с помощью связок И (
где А — имя некоторого атрибута, принимающего значения из домена D; a — константа, взятая из того же домена D,
где А, В — имена некоторых Тогда результатом операции выбора, или фильтрации, заданной на отношении R в виде булевского выражения, определенного на атрибутах отношения R, называется отношение
Операция фильтрации является одной из основных при работе с реляционной моделью данных. Условие α может быть сколь угодно сложным. Проекция Следующей специальной операцией является проекция. Пусть R — отношение, SR = (A1,..., An) — схема отношения R. Обозначим через B подмножество [ Ai ]; При этом пусть B1 — множество атрибутов из { Ai}, не вошедших в B. Если B = {A1i, Ai2,..., Aik}, B = {A1, A2j,..., Akj} и то r [B], s = < a1j, a2j,..., amj >; Проекцией отношения R на набор атрибутов В, обозначаемой R[B], называется отношение со схемой, соответствующей набору атрибутов В SR[B] = B, содержащему кортежи, получаемые из кортежей исходного отношения R путем удаления из них значений, не принадлежащих атрибутам из набора В. R[B] = { r[B] } По определению отношений все дублирующие кортежи удаляются из результирующего отношения. Операция проекции, называемая иногда также операцией вертикального выбора, позволяет получить только требуемые характеристики моделируемого объекта. Чаще всего проекция употребляется как промежуточный шаг в операциях горизонтального выбора, или фильтрации. Кроме того, она используется самостоятельно на заключительном этапе получения ответа на запрос.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 810; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.23.59 (0.01 с.) |

 , допустима для любых двух отношений. Но прежде чем определить саму операцию, введем дополнительно понятие конкатенации, или сцепления, кортежей.
, допустима для любых двух отношений. Но прежде чем определить саму операцию, введем дополнительно понятие конкатенации, или сцепления, кортежей.
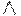 ), ИЛИ (
), ИЛИ ( ), НЕ (
), НЕ ( ) и, возможно, скобок. В качестве термов сравнения допускаются:
) и, возможно, скобок. В качестве термов сравнения допускаются: ; oc — одна из допустимых для данного домена D операций сравнения;
; oc — одна из допустимых для данного домена D операций сравнения; -сравнимых атрибутов, то есть атрибутов, принимающих значения из одного и то же домена D.
-сравнимых атрибутов, то есть атрибутов, принимающих значения из одного и то же домена D. , включающее те кортежи из исходного отношения, для которых истинно условие выбора или фильтрации:
, включающее те кортежи из исходного отношения, для которых истинно условие выбора или фильтрации:
 .
. ,
, .
.


