
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярное и векторное произведение векторовСодержание книги
Поиск на нашем сайте
Скалярное произведение двух векторов
где Для острого угла между векторами ( Единичные базисные векторы прямоугольной декартовой системы координат удовлетворяют соотношениям:
Из определения скалярного произведения (4.8) следует, что угол между векторами
Свойства скалярного произведения:
Пример. Вычислить ◄ Используя свойства скалярного произведения, имеем =
Пример. Даны координаты вершин треугольника на плоскости:
Если векторы Свойства векторного произведения:
Базисные единичные векторы декартовой прямоугольной системы координат удовлетворяют следующим соотношениям:
Если векторы
Смешанным (векторно – скалярным) произведением векторовназывается произведение
Если векторы
Пример. Даны координаты вершин треугольника:
Таким образом,
Пример. Найти объем параллелепипеда, построенного на векторах ◄ Искомый объем найдем по формуле (4.13). Вычисляем смешанное произведение данных векторов:
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 259; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.134.161 (0.006 с.) |

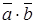 (обозначают также
(обозначают также 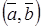 ) есть скаляр (число)
) есть скаляр (число)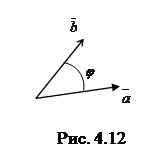
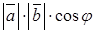 , (4.8)
, (4.8)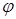 – угол между векторами
– угол между векторами 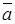 и
и 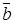 (рис. 4.12).
(рис. 4.12).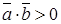 , а для тупого –
, а для тупого – 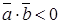 . Если они взаимно перпендикулярны
. Если они взаимно перпендикулярны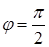 ), то
), то 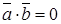 . Для коллинеарных векторов
. Для коллинеарных векторов 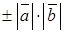 , где “+” для однонаправленных векторов, а “–“ ― для противоположно направленных. В частности
, где “+” для однонаправленных векторов, а “–“ ― для противоположно направленных. В частности 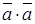 =
= 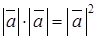 , что позволяет записать длину вектора
, что позволяет записать длину вектора 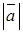 =
= 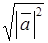 (отсюда другое название длины вектора – «модуль вектора»).
(отсюда другое название длины вектора – «модуль вектора»).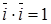 ,
, 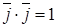 ,
, 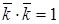 ,
, 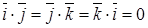 . Используя эти соотношения, не трудно получить, что если векторы
. Используя эти соотношения, не трудно получить, что если векторы 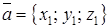 ,
, 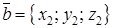 , то их скалярное произведение
, то их скалярное произведение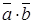 =
= 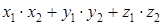 . (4.9)
. (4.9)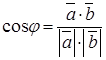 . (4.10)
. (4.10)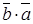 ;
; 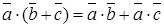 ;
;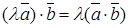 ;
; 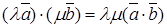 ;
;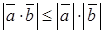 .
.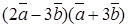 , если
, если 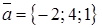 ,
, 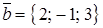 .
.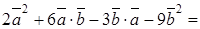
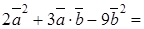
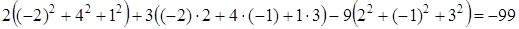 .►
.►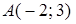 ,
, 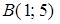 ,
, 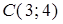 . Найти угол в треугольнике при вершине
. Найти угол в треугольнике при вершине 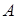 и длину стороны
и длину стороны 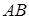 .
.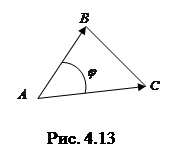 ◄ Проведем из вершины
◄ Проведем из вершины  и
и  (рис. 4.13). Тогда угол
(рис. 4.13). Тогда угол 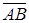 и
и 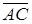 , а длина стороны
, а длина стороны 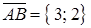 ,
, 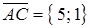 . Согласно формуле (.10)
. Согласно формуле (.10) 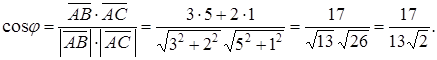 Длина стороны
Длина стороны 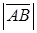 =
= 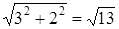 . ►
. ►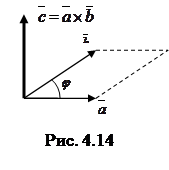 Векторное произведение
Векторное произведение 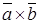 (другое обозначение
(другое обозначение 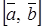 ) двух векторов
) двух векторов 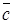 , модуль которого
, модуль которого 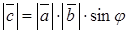 (т. е. равен площади параллелограмма, построенного на векторах
(т. е. равен площади параллелограмма, построенного на векторах 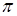 (рис 4.14). Из этого определения векторного произведения следует, что векторы
(рис 4.14). Из этого определения векторного произведения следует, что векторы 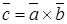 образуют правую систему.
образуют правую систему.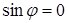 ), то
), то 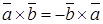 ;
; 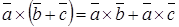 ;
; 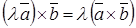 ;
;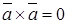 ;
; 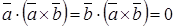 .
.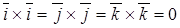 ;
; 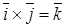 ;
; 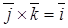 ;
; 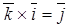 .
.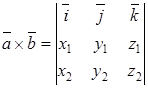 . (4.11)
. (4.11)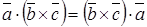 , результатом которого является скаляр (число). Для компланарных векторов их смешанное произведение
, результатом которого является скаляр (число). Для компланарных векторов их смешанное произведение 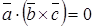 . Если векторы
. Если векторы 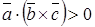 , если – левую, то
, если – левую, то 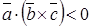 .
.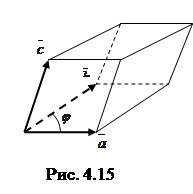 Смешанное произведение
Смешанное произведение 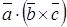 равно объему параллелепипеда
равно объему параллелепипеда 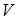 , построенного на векторах
, построенного на векторах 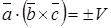 . (4.12)
. (4.12)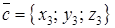 , то их смешанное произведение
, то их смешанное произведение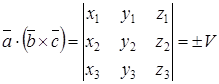 (4.13)
(4.13)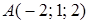 ,
, 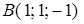 ,
, 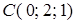 . Найти площадь
. Найти площадь 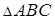 .
.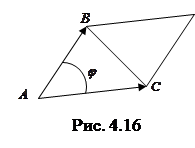 ◄ Направим из вершины
◄ Направим из вершины 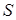
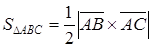 . Находим координаты векторов:
. Находим координаты векторов: 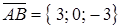 ,
, 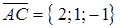 . По формуле (4.11) находим векторное произведение
. По формуле (4.11) находим векторное произведение 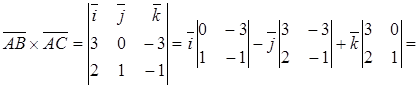
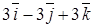 =
= 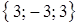 .
.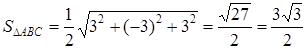 (кв. ед.). ►
(кв. ед.). ►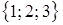 ,
, 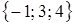 ,
, 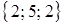 .
.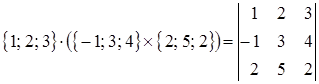 =
=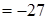 . Объем параллелепипеда
. Объем параллелепипеда 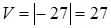 . ►
. ►


