
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 14 Основные теоремы и формулы теории вероятностейСодержание книги
Поиск на нашем сайте
Лекция 3.14.1 «Условные вероятности. Вероятности сложных событий» Учебные вопросы: 1. Условные вероятности. Независимость событий. Формулы умножения и сложения вероятностей 2. Формула полной вероятности 3. Формула Байеса
Условные вероятности. Независимость событий. Формулы умножения и сложения вероятностей Условные вероятности. Аксиоматически определенную выше вероятность можно назвать безусловной вероятностью, подчеркивая этим, что она не зависит ни от каких дополнительных условий, кроме фиксированного комплекса условий Пусть в опыте, соответствующему некоторому комплексу условий, могут произойти случайные события Пусть
Условную вероятность
Пример. При бросании правильной игральной кости стало известно, что выпало четное число очков. Какова вероятность того, что выпала: а) двойка; б) пятерка? ◄ Исходное множество элементарных исходов для данного опыта
На практике для вычисления условной вероятности
Пример. В условиях предыдущего примера новым множеством исходов будет
Независимость событий Понятие условной вероятности позволяет в свою очередь ввести в математической модели понятие независимости. Будем считать, что событие
Если События
События
Если (7) выполняется только при Формулы (6) и (7) позволяют выделять независимые события в тех случаях, когда построена формализованная вероятностная модель случайного опыта и вероятности всех рассматриваемых событий определены. Однако далеко не всегда события, независимые в таком теоретико-вероятностном смысле, являются независимыми и в реальности. На практике в любых сомнительных случаях обычно стараются принять меры для объективной проверки гипотезы о независимости событий, основываясь на теоретико-вероятностной независимости, введенной равенствами (6) и (7), с причинной независимостью реальных событий. Решение подобных задач, основанное на применении методов проверки статистических гипотез, рассматривается в математической статистике.
Пример. В группе 25 студентов. Из них 10 человек курят, 13 носят очки, а 8 и курят и носят очки. Наудачу выбирается один студент. События: ◄ Так как Необходимо отметить, что полученный вывод справедлив лишь для данного частного эксперимента, и следует остерегаться распространять его на всех студентов вообще. Хотя гипотеза о зависимости между курением и состоянием зрения кажется разумной, для ее подтверждения необходимо было бы провести статистическое обследование всех студентов на определенной территории, которое включало бы проверку зрения у каждого и регистрацию длительности и интенсивности курения для тех, кто курит. Полученные статистические данные позволили бы на основе определенного критерия подтвердить либо отвергнуть наличие статистической зависимости между курением и состоянием зрения в той группе населения, которую составляют студенты. ►
Вероятности сложных событий Сложным событием называется наблюдаемое событие, выраженное через другие наблюдаемые в том же опыте события с помощью допустимых алгебраических операций. Записав равенство (4) в виде
получаем так называемую формулу умножения вероятностей. Если оба события
Формула (9) позволяет находить вероятности совместного наступления событий Из (9) по индукции нетрудно получается формула умножения для произвольного числа событий:
Для вероятности наступления хотя бы одного из двух событий
Если события
Пример. В продукции предприятия брак составляет 5% от общего объема выпускаемых изделий. Для контроля качества случайно отобрано 20 изделий. Найти вероятность того, что среди них будет хотя бы одно бракованное. ◄ Обозначим через
Формула полной вероятности Пусть
События
Пример. Партия изделий, среди которых 5% дефектных, поступила на проверку. Схема проверки такова, что с вероятностью 0,95 обнаруживается дефект (если он есть) и существует ненулевая вероятность 0,03 того, что годное изделие будет признано дефектным. Найти вероятность того, что случайно выбранное из партии изделие будет признано дефектным. ◄ Нас интересует событие
Формула полной вероятности Пусть {
которая является следствием формулы полной вероятности (13). Формулу Байеса иногда называют формулой гипотез. Она позволяет «переоценить» вероятность каждой из гипотез после поступления новой информации относительно наступления тех или иных наблюдаемых событий. Формула Байеса может служить также для принятия решений в тех случаях, когда гипотезы
Пример. В условиях предыдущего примера случайно выбранное из партии изделие было признано дефектным. Какова вероятность того, что на самом деле изделие годно? ◄ В обозначениях предыдущего примера требуется найти
Пример. Из урны, содержащей 4 белых и 9 черных шаров, один шар неизвестного цвета был утерян. Какова вероятность того, что шар, извлеченный из урны после утери, окажется белым? Какова вероятность того, что утерян черный шар, если после утери извлечен белый шар? ◄ Нас интересует событие Лекция 3.14.2 «Последовательность испытаний» Учебные вопросы: 1. Последовательность испытаний 2. Последовательность независимых испытаний. Схема Бернулли 3. Предельные теоремы в схеме Бернулли
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.18.73 (0.01 с.) |

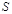 , которым характеризуется опыт.
, которым характеризуется опыт. и
и  . Допустим также, что стало известно, что осуществилось событие
. Допустим также, что стало известно, что осуществилось событие 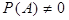 . Условная вероятность
. Условная вероятность 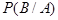 наступления события
наступления события 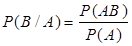 . (4)
. (4)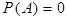 условная вероятность
условная вероятность 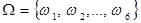 , где
, где 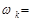 {число выпавших очков равно
{число выпавших очков равно 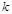 }, содержит
}, содержит 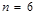 исходов. Три из них благоприятствуют событию
исходов. Три из них благоприятствуют событию 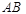 , где
, где  , где
, где  ={выпала пятерка}, равно нулю. По формуле (4) получаем:
={выпала пятерка}, равно нулю. По формуле (4) получаем: 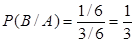 ,
, 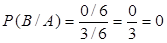 . ►
. ►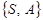 . В этом новом комплексе условий получают соответствующее ему множество элементарных исходов
. В этом новом комплексе условий получают соответствующее ему множество элементарных исходов 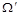 . Безусловная вероятность осуществления события
. Безусловная вероятность осуществления события 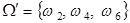 . Один из этих исходов благоприятствует событию
. Один из этих исходов благоприятствует событию 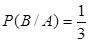 ,
, 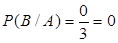 .
.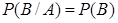 . (5)
. (5)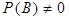 , то из равенств (74) и (5) следует, что
, то из равенств (74) и (5) следует, что 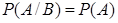 , т. е. независимость является взаимным свойством: если
, т. е. независимость является взаимным свойством: если 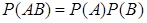 . (6)
. (6)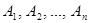 называются взаимно независимыми (или независимыми в совокупности, или просто независимыми), если для любого набора из
называются взаимно независимыми (или независимыми в совокупности, или просто независимыми), если для любого набора из  событий (
событий ( ) выполняется равенство
) выполняется равенство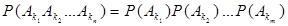 ,
, 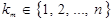 . (7)
. (7)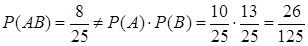 , т. е. условие (6) независимости не выполняется, делаем вывод, что события
, т. е. условие (6) независимости не выполняется, делаем вывод, что события 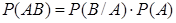 , (8)
, (8)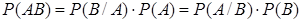 . (9)
. (9)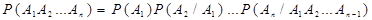 . (10)
. (10)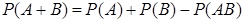 . (11)
. (11)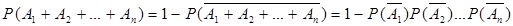 . (12)
. (12)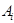 события
события 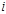 - ое по счету отобранное изделие бракованное},
- ое по счету отобранное изделие бракованное}, 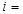 1, 2, …, 20. По условию вероятность того, что изделие в продукции предприятия является бракованным, равна
1, 2, …, 20. По условию вероятность того, что изделие в продукции предприятия является бракованным, равна 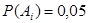 . Очевидно, что нас интересует событие
. Очевидно, что нас интересует событие 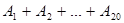 . В условиях стабильного технологического процесса производства можно считать, что события
. В условиях стабильного технологического процесса производства можно считать, что события 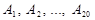 независимы в совокупности. Учитывая, что
независимы в совокупности. Учитывая, что 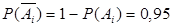 , по формуле (12) получаем
, по формуле (12) получаем 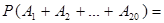
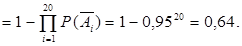 ►
►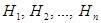 – наблюдаемые события для данного опыта, причем система множеств {
– наблюдаемые события для данного опыта, причем система множеств {  этого опыта, т. е. выполняются следующие условия:
этого опыта, т. е. выполняются следующие условия: 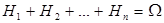 ,
, 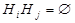 при любых
при любых 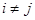 ,
, 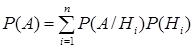 . (13)
. (13)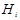 принято называть гипотезами по отношению к событию
принято называть гипотезами по отношению к событию 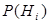 , для которых должно выполняться равенство
, для которых должно выполняться равенство 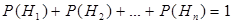 , трактуются как априорные (доопытные) вероятности гипотез. Для вычисления вероятности интересующего нас события по формуле (13) важно удачно подобрать набор гипотез. Если зависимость события
, трактуются как априорные (доопытные) вероятности гипотез. Для вычисления вероятности интересующего нас события по формуле (13) важно удачно подобрать набор гипотез. Если зависимость события 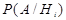 не могут быть просто вычислены, то такое разбиение не принесет практической пользы при решении задачи.
не могут быть просто вычислены, то такое разбиение не принесет практической пользы при решении задачи.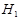 ={поступившее на проверку изделие дефектно},
={поступившее на проверку изделие дефектно}, 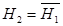 ={поступившее на проверку изделие годно}. Безусловные априорные вероятности этих гипотез равны
={поступившее на проверку изделие годно}. Безусловные априорные вероятности этих гипотез равны 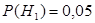 ,
, 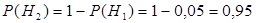 . Условные вероятности заданы в условии задачи:
. Условные вероятности заданы в условии задачи: 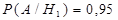 ,
, 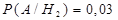 . По формуле полной вероятности получаем
. По формуле полной вероятности получаем 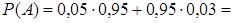
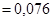 . ►
. ►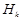 при условии, что событие
при условии, что событие 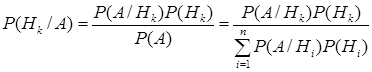 , (14)
, (14)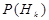 и соответствующие условные вероятности
и соответствующие условные вероятности 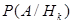 ,
, 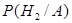 (апостериорную условную вероятность гипотезы
(апостериорную условную вероятность гипотезы 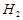 ). По формуле Байеса имеем
). По формуле Байеса имеем 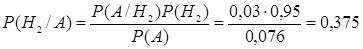 . Таким образом, апостериорная условная вероятность того, что изделие на самом деле годное, если известно, что оно было признано дефектным, существенно меньше априорной вероятности гипотезы
. Таким образом, апостериорная условная вероятность того, что изделие на самом деле годное, если известно, что оно было признано дефектным, существенно меньше априорной вероятности гипотезы 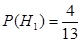 ,
, 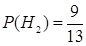 ,
, 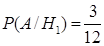 ,
, 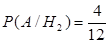 . По формуле полной
. По формуле полной 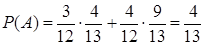 . Отметим, что вероятность извлечения белого шара из урны до утери также равна
. Отметим, что вероятность извлечения белого шара из урны до утери также равна 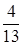 . Для нахождения апостериорной условной вероятности гипотезы
. Для нахождения апостериорной условной вероятности гипотезы 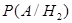 используем формулу Байеса:
используем формулу Байеса: 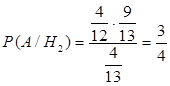 .►
.►


