
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел II: математический анализСодержание книги
Поиск на нашем сайте
Тема 6 Производная и дифференциал
Лекция 2.6.1 «Функция. Предел. Непрерывность» Учебные вопросы: 1. Функция 2. Предел. Непрерывность
Функция Постоянная величина – это величина, сохраняющая одно и то же значение. Если величина сохраняет постоянное значение лишь в условиях данного процесса, то она называется параметром. Переменная – это величина, которая может принимать различные числовые значения. Если каждому элементу При этом х называется независимой переменной или аргументом, y – зависимой переменной, а буква Множество Х называется областью определения (существования) функции, а множество Y – областью значений функции. Способы заданий функций: 1. Аналитический способ. В этом случае функция задается формулой вида 2. Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента х и соответствующие значения функции 3. Графический способ состоит в изображении графика функции – множества точек плоскости 4. Словесный способ, если функция описывается правилом ее составления. Основные свойства функций: 1. Четность и нечетность. Функция Пример. Функция График четной функции симметричен относительно оси ординат, а нечетной функции – относительно начала координат. 2.
Монотонность. Функция 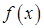 называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции (см. рисунок). Если для любых называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции (см. рисунок). Если для любых 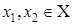 , , 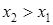 , , 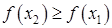 – функция – функция 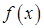 возрастающая, возрастающая, 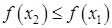 – функция – функция 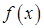 убывающая. Возрастающие и убывающие функции называются монотонными. убывающая. Возрастающие и убывающие функции называются монотонными.
3. Ограниченность. Функция 4. Периодичность. Функция
Функция называется явной, если она задана формулой, правая часть которой не содержит зависимой переменной: Функция называется неявной, если она задана уравнением Пусть Можно доказать, что для любой строго монотонной функции
Например, Основные элементарные функции: 1. Степенная функция: 2. Показательная функция: 3. Логарифмическая функция: 4. Тригонометрические функции: 5. Обратные тригонометрические функции: Пусть задан график функции 1. График функции 2. График функции 3. График функции - растянутый в m раз вдоль оси Oy, при - сжатый в m раз вдоль оси Oy, при - растянутый в m раз вдоль оси Oy и отраженный зеркально относительно оси Ox, при - сжатый в m раз вдоль оси Oy и отраженный зеркально относительно оси Ox, при 4. График функции - сжатый в k раз вдоль оси Ox, при - растянутый в k раз вдоль оси Ox, при - сжатый в k раз вдоль оси Ox и отраженный зеркально относительно оси Oy, при
- растянутый в k раз вдоль оси Ox и отраженный зеркально относительно оси Oy, при
Предел. Непрерывность Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число Числа Примеры: 2, 4, 6, …, 2 n, … (монотонная неограниченная последовательность четных чисел); 1, 0, 1, 0, … (немонотонная ограниченная последовательность чередующихся чисел 0 и 1). Число А называется пределом числовой последовательности
Предел числовой последовательности обозначается Смысл определения: для достаточно больших n члены последовательности Число А называется пределом функции y = f(x) при х, стремящемся к бесконечности, если для любого e > 0 найдется такое S > 0, что для всех | х | > S верно неравенство | f(x) – A | < e (7.2) Предел функции обозначается Это предел функции в бесконечности. Число А называется пределом функции f(x) при х ® х0, если для любого e > 0 найдется такое d = d(e) > 0, что для всех x ¹ x 0, | х – x0 | < d выполняется неравенство | f(x) – A | < e. Смысл определения: для всех значений х, достаточно близких к х0, значения f(x) как угодно мало отличаются от числа А. Замечание 1. Определение предела не требует существования функции в самой точке х0, поскольку предполагается, что х стремится к х0, но не достигает значения х0. Поэтому наличие или отсутствие предела при х ® х0 определяется поведением функции в окрестности точки х0, но не связано с существованием функции в самой точке х0. Замечание 2. Если при х ® х0 переменная х принимает только значения, меньшие х0, и при этом функция f(x) стремится к некоторому числу А, то говорят об одностороннем пределе функции слева:
Аналогично, при х ® х0, х > х0 говорят об одностороннем пределе функции справа, т.е:
При этом если Функция a(x) называется бесконечно малой величиной при
Связь бесконечно малых величин с пределами функций определяется теоремами: Теорема: Если Обратная теорема: Если функцию f(x) можно представить как сумму числа А и бесконечно малой a (x) при х ® х0 (¥), то число А есть предел этой функции при х ® х0 (¥), т.е.
Свойства бесконечно малых величин: 1. Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая. 2. Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая. 3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая. Замечание. Свойство 3 не рассматривает предел отношения двух бесконечно малых a (x) и b (x) из-за его неопределенности. Этот предел
Функция f(x) называется бесконечно большой величиной при х ® х0, если для любого M > 0 найдется такое d > 0 (d (M)), что для всех x ¹ x 0, | х – x0 | < d будет верно: Свойства бесконечно больших величин: 1. Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая. 2. Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая. 3. Частное от деления бесконечно большой величины на функцию, имеющую предел в точке х0, есть величина бесконечно большая. Связь между бесконечно малыми и бесконечно большими величинами устанавливает следующая теорема: Теорема: Если a (x) есть бесконечно малая при х ® х0 (¥), то функция Основные теоремы о пределах Пусть f(x) и j (x) – функции, для которых существуют пределы при х ® х0 (¥):
Тогда имеют место следующие теоремы о пределах: 1. Функция не может иметь более одного предела. 2. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций:
3. Предел произведения конечного числа функций равен произведению пределов этих функций:
В частности, постоянный множитель можно выносить за знак предела:
4. Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю):
Пример. Вычислить предел ◄ Пределы числителя и знаменателя существуют и предел знаменателя не равен нулю. Пользуясь теоремой о пределе частного, получаем:
Пример. Вычислить ◄ Теорему о переделе частного здесь применять нельзя, т.к. числитель и знаменатель конечного предела не имеют. Имеем неопределенность
Замечательные пределы Первый замечательный предел:
Второй замечательный предел:
где
Пример. Вычислить ◄ Для раскрытия подобных неопределенностей
Непрерывность функции. Функция f (x) называется непрерывной в точке х0, если она удовлетворяет следующим условиям: 1) она определена в точке 2) она имеет конечный предел функции при х ® х0; 3) этот предел равен значению функции в точке х0, т.е. Например, в точке х = 0 функция
в точке х = 0 не является непрерывной из-за отсутствия предела при х ® 0, хотя существуют пределы слева и справа (см. рис.). Точка Точка разрыва 1-го рода: существуют конечные односторонние пределы функции слева и справа при х ® х0, не равные друг другу. В качестве примера можно указать точку х = 0 для рассмотренной выше функции Точка разрыва 2-го рода: хотя бы один из односторонних пределов равен бесконечности или не существует. В качестве примера можно указать точку х = 0 для функции Свойства функций непрерывных в точке: 1. Если функции 2. Если функция y = f (x) непрерывна в точке х0 и f(x0) > 0, то существует такая окрестность точки x 0, в которой и f(x) > 0. 3. Если функция y = f (u) непрерывна в точке u0 и f(x0) > 0, а функция Функция y = f (x) называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка. Свойства функций непрерывных на отрезке: 1. Если функция y = f (x) непрерывна на отрезке [ a, b ], то она ограничена на этом отрезке. 2. Если функция y = f (x) непрерывна на отрезке [ a, b ], она достигает на этом отрезке наименьшего значения m и наибольшего значения M. 3. Если функция y = f (x) непрерывна на отрезке [ a, b ] и ее значения на концах отрезка f(a) и f(b) имеют противоположные знаки, то внутри отрезка найдется точка x Î (a, b) такая, что f (x)=0.
Лекция 2.6.2 «Производная. Дифференциал» Учебные вопросы: 1. Производная 2. Дифференциал
Производная Производной от функции
Другие обозначения производной: Дифференцирование функции – это нахождение производной этой функции. Если функция имеет в точке x производную (конечную), то она называется дифференцируемой в этой точке.
Механический смысл: производная пути по времени
Производительность труда в момент Теорема. Если функция Обратная теорема, вообще говоря, не верна, т.е. непрерывная функция может быть не дифференцируемой в точке Правила дифференцирования 1. Производная константы равна нулю, т.е. 2. Производная аргумента равна 1, т.е. 3. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, т.е.
4. Производная произведения двух дифференцируемых функций:
Следствие. Постоянный множитель можно выносить за знак производной: 5. Производная частного двух дифференцируемых функций:
при условии, что 6. Производная сложной функции
Теорема. Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции, т.е. Производная логарифмической функции:
Производная показательной функции:
Производная степенной функции:
Производные тригонометрических функций:
Производные высших порядков Производная Производной n -го порядка называется производная от производной (n -1)-го порядка. Обозначается: Механический смысл 2-й производной: 2-ая производная пути во времени
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.157.233 (0.009 с.) |

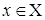 ставится в соответствие вполне определенный элемент
ставится в соответствие вполне определенный элемент 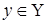 , то говорят, что на множестве Х задана функция
, то говорят, что на множестве Х задана функция 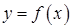 .
.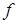 обозначает закон соответствия.
обозначает закон соответствия.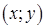 , абсциссы которых есть значения аргументов х, а ординаты – соответствующие им значения функции
, абсциссы которых есть значения аргументов х, а ординаты – соответствующие им значения функции 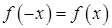 , и нечетной, если
, и нечетной, если 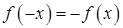 . В противном случае функция
. В противном случае функция  – четная,
– четная,  – нечетная,
– нечетная, 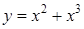 – общего вида.
– общего вида.
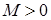 , что для любого
, что для любого 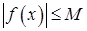 .
.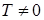 , если для любого
, если для любого 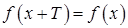 .
.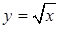 ,
, 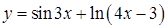 .
.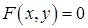 , не разрешенным относительно зависимой переменной:
, не разрешенным относительно зависимой переменной: 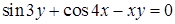 .
.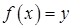 . Тогда полученная функция
. Тогда полученная функция 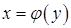 , определенная на промежутке Y с областью значений Х, называется обратной для функции
, определенная на промежутке Y с областью значений Х, называется обратной для функции 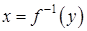 (это не степень!). Примеры: для функции
(это не степень!). Примеры: для функции 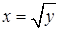 , для функции
, для функции 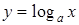 обратной будет
обратной будет 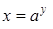
 выраженном через
выраженном через 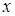 ), то они будут симметричны относительно биссектрисы 1-го и 3-го координатных углов (прямой, проходящей под углом
), то они будут симметричны относительно биссектрисы 1-го и 3-го координатных углов (прямой, проходящей под углом 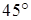 из начала координат) (см. рис.)..
из начала координат) (см. рис.)..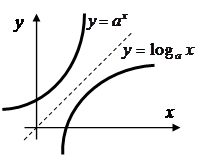 Пусть функция
Пусть функция 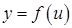 есть функция от переменной u, определенной на множестве U с областью значений Y, а переменная u, в свою очередь, является функцией
есть функция от переменной u, определенной на множестве U с областью значений Y, а переменная u, в свою очередь, является функцией 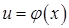 от переменной х, определенной на множестве Х с областью значений U. Тогда
от переменной х, определенной на множестве Х с областью значений U. Тогда 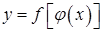 называется сложной функцией (композицией функций, функцией от функции).
называется сложной функцией (композицией функций, функцией от функции).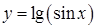 – сложная функция, т.к. ее можно представить в виде
– сложная функция, т.к. ее можно представить в виде 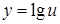 , где
, где 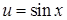 .
.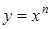 (и ее частные виды
(и ее частные виды 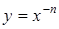 ,
, 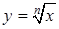 ).
).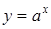 .
.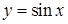 ,
,  ,
, 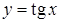 ,
, 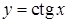 .
.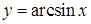 ,
, 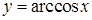 ,
, 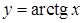 ,
, 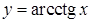 .
.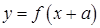 есть график
есть график 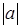 единиц вдоль оси Oх; при
единиц вдоль оси Oх; при 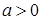 – влево, при
– влево, при 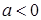 – вправо.
– вправо.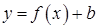 есть график
есть график 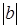 единиц вдоль оси Oy; при
единиц вдоль оси Oy; при 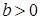 – вверх, при
– вверх, при 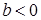 – вниз.
– вниз.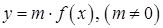 есть график
есть график 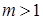 ;
;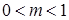 ;
;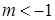 ;
;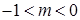 .
.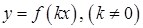 есть график
есть график 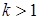 ;
;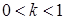 ;
;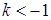 ;
;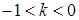 .
.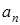 ,то говорят, что задана числовая последовательность
,то говорят, что задана числовая последовательность 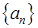 :
: 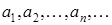 . Другими словами, числовая последовательность – это функция натурального аргумента
. Другими словами, числовая последовательность – это функция натурального аргумента 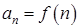 .
.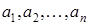 называются членами последовательности, а число
называются членами последовательности, а число 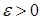 найдется такой номер
найдется такой номер 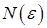 , зависящий от
, зависящий от 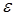 , что для всех членов данной последовательности с номерами
, что для всех членов данной последовательности с номерами 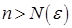 верно неравенство
верно неравенство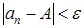 (7.1)
(7.1)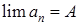 или
или 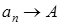 при
при 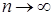 . Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.
. Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.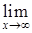 f(x) = A, или f(x) ® A при х ® ¥.
f(x) = A, или f(x) ® A при х ® ¥.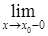 f(x) = A
f(x) = A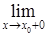 f(x) = A
f(x) = A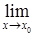 f(x) = A.
f(x) = A.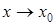 или при
или при 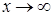 , если ее предел равен нулю:
, если ее предел равен нулю: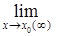 a (x) = 0
a (x) = 0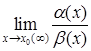 может быть равен нулю, числу А ¹ 0 или бесконечности ¥. В первом случае a (x) называется бесконечно малой более высокого порядкамалости чем b (x). Это записывается так: a (x) = o(b (x)) при х ® х0 (¥), т.е. “ a (x) есть о малое от b (x)”. Во втором случае a (x) и b (x) одного порядкамалости (“ a (x) есть О большое от b (x)” или b (x) = O(a (x))). В третьем случае a (x) более низкого порядка малости чем b (x). При
может быть равен нулю, числу А ¹ 0 или бесконечности ¥. В первом случае a (x) называется бесконечно малой более высокого порядкамалости чем b (x). Это записывается так: a (x) = o(b (x)) при х ® х0 (¥), т.е. “ a (x) есть о малое от b (x)”. Во втором случае a (x) и b (x) одного порядкамалости (“ a (x) есть О большое от b (x)” или b (x) = O(a (x))). В третьем случае a (x) более низкого порядка малости чем b (x). При 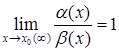 a (x) и b (x) называются эквивалентными и пишут a (x)» b (x).
a (x) и b (x) называются эквивалентными и пишут a (x)» b (x).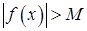 .
.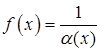 является бесконечно большой при х ® х0 (¥). Обратно, если функция a (x) есть бесконечно большая при х ® х0 (¥), то функция
является бесконечно большой при х ® х0 (¥). Обратно, если функция a (x) есть бесконечно большая при х ® х0 (¥), то функция 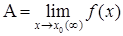 ,
, 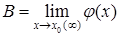
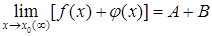
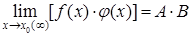
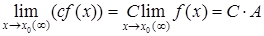
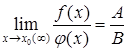 (B ¹ 0)
(B ¹ 0)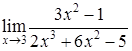 .
.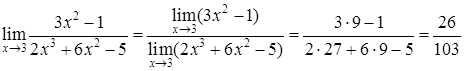 . ►
. ►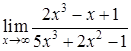 .
.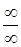 . В подобных случаях для раскрытия неопределенности целесообразно числитель и знаменатель разделить на степень х с наивысшим показателем, а затем перейти к пределу:
. В подобных случаях для раскрытия неопределенности целесообразно числитель и знаменатель разделить на степень х с наивысшим показателем, а затем перейти к пределу: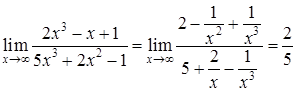 . ►
. ►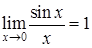
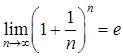 ,
, –число Эйлера, которое является основанием для натуральных логарифмов. Последний предел можно записать в других формах:
–число Эйлера, которое является основанием для натуральных логарифмов. Последний предел можно записать в других формах: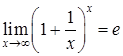 ,
,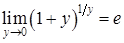 .
.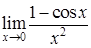 .
.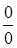 используется первый замечательный предел:
используется первый замечательный предел: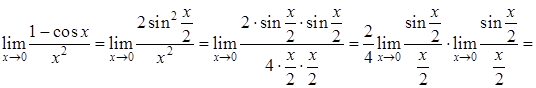
 .►
.►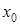 ,т.е. существует f(х0);
,т.е. существует f(х0);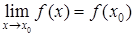
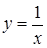 не является непрерывной (нарушено 1-е условие).
не является непрерывной (нарушено 1-е условие).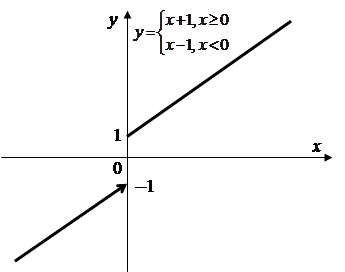 Функция, заданная выражением:
Функция, заданная выражением: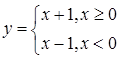
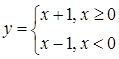 .
.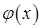 непрерывны в точке
непрерывны в точке 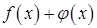 , произведение
, произведение 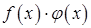 и частные
и частные 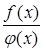 (
(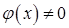 ) являются функциями, непрерывными в точке
) являются функциями, непрерывными в точке 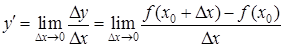 .
.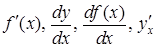 .
.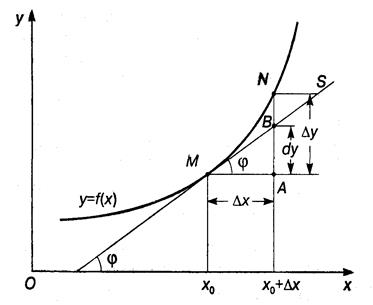 Геометрический смысл производной: производная
Геометрический смысл производной: производная 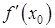 равна тангенсу угла между осью Ox и касательной, проведенной к графику функции
равна тангенсу угла между осью Ox и касательной, проведенной к графику функции 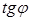 (см. рис.).
(см. рис.).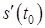 есть скорость точки в момент
есть скорость точки в момент 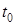 т.е.
т.е. 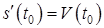 .
.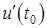 .
.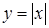 в точке
в точке 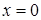 .
.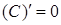 , где С - const.
, где С - const.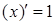 .
.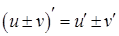
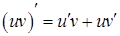
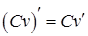 , где С - const.
, где С - const.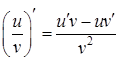 .
.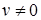 .
.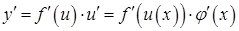
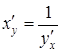 .
.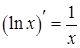 ;
; 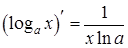 .
.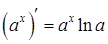 ;
; 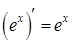
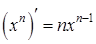 .
. 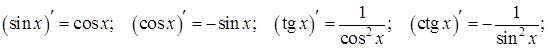
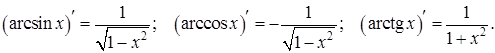
 Производная неявной функции
Производная неявной функции 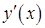 :
: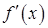 называется производной 1-го порядка. Однако производная сама является функцией, которая также может иметь производную.
называется производной 1-го порядка. Однако производная сама является функцией, которая также может иметь производную.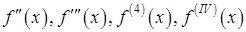 и т.д.
и т.д.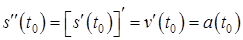 равна ускорению точки в момент
равна ускорению точки в момент 


