
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3 Системы линейных алгебраических уравненийСодержание книги
Поиск на нашем сайте
Лекция 1.3.1 «Системы линейных алгебраических уравнений: общая теория» Учебные вопросы: 1. Системы линейных алгебраических уравнений. Теорема Кронекера - Капелли 2. Применение определителей к исследованию и решению систем линейных уравнений. Формулы Крамера
Системы линейных алгебраических уравнений. Теорема Кронекера - Капелли Рассмотрим систему m линейных алгебраических уравнений с n неизвестными
Здесь Система может не иметь решений (уравнения несовместны), иметь единственное решение (единственный набор значений неизвестных Составим из коэффициентов
и назовем ее матрицей системы. Матрицу
Теорема Кронекера - Капелли: система m линейных алгебраических уравнений с n неизвестными имеет решение в том и только в том случае, если матрица системы и расширенная матрица системы имеют один и тот же ранг Единственное решение существует, если Если обе матрицы имеют ранг Если обе матрицы имеют ранг Пример. Исследовать систему линейных уравнений
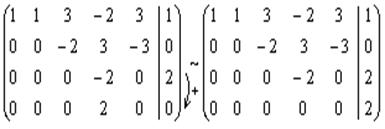
◄ Составим расширенную матрицу системы и с помощью указанных около нее элементарных преобразований найдем одновременно ранги обеих матриц:
Прибавив к четвертой строке последней матрицы третью строку, получаем
Ранг матрицы системы равен трем, так как ее преобразованная матрица имеет три ненулевых строки, а ранг расширенной матрицы равен четырем. Тогда согласно теореме Кронекера-Капелли система не имеет решений. ►
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.242.39 (0.005 с.) |

 :
: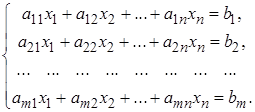
 - коэффициенты системы (
- коэффициенты системы (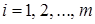 - номер уравнения (строки),
- номер уравнения (строки), 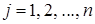 - номер неизвестной, при которой данный коэффициент стоит),
- номер неизвестной, при которой данный коэффициент стоит), 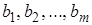 - свободные члены системы. Если все свободные члены равны нулю (
- свободные члены системы. Если все свободные члены равны нулю (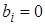 ,
, 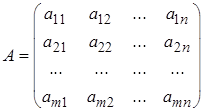
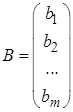 называют матрицей-столбцом из свободных членов, а матрицу
называют матрицей-столбцом из свободных членов, а матрицу  – матрицей-столбцом из неизвестных. Матрицу
– матрицей-столбцом из неизвестных. Матрицу 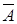 , полученную из матрицы
, полученную из матрицы 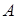 добавлением столбца свободных членов, называют
добавлением столбца свободных членов, называют  .
. . В противном случае уравнения несовместны.
. В противном случае уравнения несовместны. .
.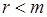 ,то уравнения системы линейно зависимы и некоторые
,то уравнения системы линейно зависимы и некоторые 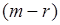 можно выразить в виде линейных комбинаций остальных
можно выразить в виде линейных комбинаций остальных 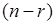 неизвестных, остающихся произвольными.
неизвестных, остающихся произвольными.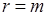 ,то уравнения системы линейно независимы.
,то уравнения системы линейно независимы.

 .
.


