
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наиболее распространенные законы распределения дискретных случайных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приведем некоторые часто встречающиеся в вероятностных моделях законы распределения дискретных случайных величин. 1○. Биномиальный закон для числа успехов
где Основные характеристики биномиального распределения: mX = np,
Пример. Вероятности рождения девочки и мальчика в первом приближении можно считать равными 0,5. Какова вероятность того, что среди ◄ Пусть Х – число мальчиков среди
Вероятность события
Вероятность события
Для подсчета вероятности события
для всех k =1, 2,…, = Найдем числовые значения полученных вероятностей при
2. Равномерное распределение на {1, 2, …, N }:
3. Распределение Пуассона. Случайная величина Х называется распределенной по закону Пуассона с параметром
Характерной особенностью распределения Пуассона является совпадение математического ожидания и дисперсии, причем
Распределение Пуассона может быть получено из биномиального распределения путем предельного перехода при
Пример. На факультете насчитывается 500 студентов. Какова вероятность того,что 1 сентября является днем рождения одновременно для ◄ Так как
Значения искомых вероятностей, соответствующих биномиальному распределению
5. Геометрическое распределение зависит от параметра
В этом случае также выполнено условие
Пример. Производится стрельба по цели до первого попадания. Вероятность попадания при каждом выстреле равна ◄ Для случайного числа произведенных выстрелов
Из этого ряда видно, что
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 621; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.012 с.) |

 при
при  независимых испытаниях в схеме Бернулли
независимых испытаниях в схеме Бернулли { X =
{ X = 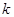 } =
} =  ,
,  – параметр распределения, равный вероятности наступления успеха в каждом отдельном испытании. Соответствующее этой формуле Бернулли распределение случайной величины
– параметр распределения, равный вероятности наступления успеха в каждом отдельном испытании. Соответствующее этой формуле Бернулли распределение случайной величины  .
.
 = npq, aX =
= npq, aX =  , eX =
, eX =  .
. наудачу отобранных новорожденных будет хотя бы один мальчик (событие
наудачу отобранных новорожденных будет хотя бы один мальчик (событие 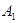 ); число мальчиков и девочек одинаково (событие
); число мальчиков и девочек одинаково (событие  ); мальчиков будет больше, чем девочек (событие
); мальчиков будет больше, чем девочек (событие  )? Получить числовые значения искомых вероятностей для
)? Получить числовые значения искомых вероятностей для  , т.е. согласно формуле (1)
, т.е. согласно формуле (1)
 , k = 0,1,…,
, k = 0,1,…,  ) = 1 -
) = 1 - 
 .
.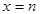 . Действительно:
. Действительно: } = Р2n, n-k
} = Р2n, n-k  =
= 
 }
}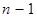 . Кроме того, нетрудно проверить, что это значение является наиболее вероятным, т.е. мода распределения dX =
. Кроме того, нетрудно проверить, что это значение является наиболее вероятным, т.е. мода распределения dX =  (1 -
(1 -  ).
). = 0,9990,
= 0,9990, 
 ,
,  > 0, если ее возможные значения равны 0, 1, 2,..., а соответствующие вероятности определяются формулой
> 0, если ее возможные значения равны 0, 1, 2,..., а соответствующие вероятности определяются формулой (3)
(3)
 при условии
при условии 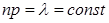 и в этом случае интерпретируется как закон «редких» явлений. Если
и в этом случае интерпретируется как закон «редких» явлений. Если  << 1, то можно считать, что случайное число студентов X, родившихся 1 сентября, подчиняется закону распределения Пуассона с параметром
<< 1, то можно считать, что случайное число студентов X, родившихся 1 сентября, подчиняется закону распределения Пуассона с параметром  = 1,36986. Поэтому по формуле (3)
= 1,36986. Поэтому по формуле (3)  Далее находим рекуррентно:
Далее находим рекуррентно:

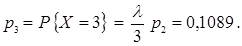
 и вычисленных с четырьмя верными знаками после запятой, таковы:
и вычисленных с четырьмя верными знаками после запятой, таковы:  ►
► ,
,  = 1 –
= 1 –  = 1.
= 1. .
.



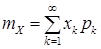 =
=  =
= 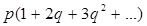 =
=  = =
= =  =
=  = =
= =  . При
. При  , т.е. среднее число выстрелов до первого попадания при данной вероятности попадания при каждом выстреле будет равно пяти. ►
, т.е. среднее число выстрелов до первого попадания при данной вероятности попадания при каждом выстреле будет равно пяти. ►


