
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
C. Случайная величина, которая может принимать любые значения внутри некоторого интервала.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
D. Случайная величина, принимающая отличные друг от друга значения, можно пронумеровать.
З А Д А Н И Е № 2 По какой формуле вычисляется математическое ожидание для дискретной случайной величины? A. B. C. D. E.
З А Д А Н И Е № 3 Какая формула используется для вычисления дисперсии случайной дискретной величины? A. B. C. D. E.
З А Д А Н И Е № 4 Выберите правильное определение дисперсии случайной дискретной величины. A. Это сумма произведений всех возможных значений случайной величины на их вероятности. B. Это величина, характеризующая отклонение случайной величины от ее среднего квадратического отклонения. C. Это произведение математического ожидания на квадрат отклонения случайной величины. D. Это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. E. Это математическое ожидание квадрата отклонения случайной величины от ее максимального значения.
З А Д А Н И Е № 5 Какие показатели, которые приведены ниже, можно отнести к случайным непрерывным величинам. A. Число больных на приеме у врача, насыщение кислородом артериальной крови, количество эритроцитов. B. Температура тела человека, артериальное давление, масса тела. C. Число молекул в выделенном объеме газа, количество эритроцитов, насыщение кислородом венозной крови. D. Температура тела человека, количество студентов в аудитории, масса тела. E. Объем газа, количество эритроцитов, насыщение кислородом венозной крови.
З А Д А Н И Е № 6 Выберите вариант ответа, в котором все показатели можно отнести к случайным дискретным величинам. A. Число больных на приеме у врача, частота пульса. B. Температура тела человека, артериальное давление, насыщение кислородом артериальной и венозной крови. C. Артериальное давление, скорость оседания эритроцитов. D. Количество эритроцитов, температура тела человека. E. Частота пульса, масса тела, объем молекулы.
З А Д А Н И Е № 7 Случайную величину Х увеличили в "а" раз. Как при этом изменится дисперсия этой случайной величины? A. Увеличится в "а" раз. B. Уменьшится на "а" раз. C. Уменьшится в "а D. Увеличится в "а
E. Не изменится.
З А Д А Н И Е № 8 Какую размерность имеет значение дисперсии случайной величины? A. Размерность случайной величины. B. Размерность квадрата случайной величины. C. Размерность куба случайной величины. D. Размерность квадратного корня случайной величины. E. Не имеет размерности.
З А Д А Н И Е № 9 Какую размерность имеет значение математического ожидания случайной величины? A. Размерность случайной величины. B. Размерность квадрата случайной величины. C. Размерность куба случайной величины. D. Размерность квадратного корня случайной величины. E. Не имеет размерности.
З А Д А Н И Е № 10 Какую размерность имеет значение среднего квадратического отклонения случайной величины? A. Размерность случайной величины. B. Размерность квадрата случайной величины. C. Размерность куба случайной величины. D. Размерность квадратного корня случайной величины. E. Не имеет размерности.
З А Д А Н И Е № 11 Почему при описании случайной величины чаще пользуются средним квадратическим отклонением, чем дисперсией? A. Для повышения точности расчетов. B. Для уменьшения относительной погрешности. C. Для приведения в соответствие размерности разброса случайной величины с размерностью самой случайной величины. D. Для уменьшения абсолютной погрешности.
З А Д А Н И Е № 12 Случайную величину Х увеличили в "а" раз. Как при этом изменится математическое ожидание этой случайной величины? A. Не изменится B. Увеличится в "а C. Уменьшится в "а" раз D. Увеличится в "а" раз E. Уменьшится в "а
ЗАДАЧИ
З А Д А Н И Е № 1 При изучении электрического сопротивления кожи до введения атропина установлен закон распределения случайной величины
Найдите математическое ожидание случайной величины. A. 2,3 B. 8,4 C. 9 D. 9,5 E. 7,2
З А Д А Н И Е № 2 Дан закон распределения значений физиологического показателя (кардиоинтервалы, сек) водителей до работы
Найдите математическое ожидание случайной дискретной величины. A. 0.24 B. 0.3 C. 0.33 D. 0.45 E. 0.28
З А Д А Н И Е № 3
Дан закон распределения значений физиологического показателя – частоты сердечных сокращений у водителей до работы по данным ЭКГ
Найдите математическое ожидание случайной дискретной величины. A. 39.4 B. 81.5 C. 76.8 D. 73.2 E. 80
З А Д А Н И Е № 4 Закон распределения диастолического давления после введения атропина представлен следующим образом
Математическое ожидание этой случайной величины принимает значение, равное 78.5. Рассчитайте дисперсию случайной величины. A. 22.5 B. 20.25 C. 18.5 D. 17.25 E. 21
З А Д А Н И Е № 5 Дан закон распределения значений физиологического показателя (мышечная сила в кг) водителей до рабочего дня
Математическое ожидание этой случайной величины принимает значение, равное 67.2. Определите дисперсию. A. 67 B. 67.96 C. 69.2 D. 72.96 E. 70.57
З А Д А Н И Е № 6 Дан закон распределения значений физиологического показателя (индекса напряжения по данным ЭКГ /лежа/) водителей после работы
Математическое ожидание этой случайной величины принимает значение, равное 35. Определите дисперсию. A. 60 B. 50 C. 55 D. 45 E. 30
З А Д А Н И Е № 7 Найти среднеквадратичное отклонение случайной величины, если ее дисперсия принимает значение, равное 4. A. 2 B. 4 C. 8 D. 16 E. 1
З А Д А Н И Е № 8 Найти среднеквадратичное отклонение случайной величины, если ее дисперсия принимает значение, равное 144. A. 9 B. 12 C. 8 D. 11 E. 25 ТЕМА: Математическая статистика (теория)
З А Д А Н И Е № 1 В каких случаях требуется знание коэффициента Стьюдента? A. Для расчета среднего значения генеральной совокупности. B. Для расчета дисперсии выборки. C. Для точечной оценки случайных величин.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2069; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.242.39 (0.011 с.) |



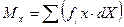


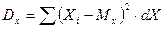




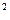 " раз.
" раз.



