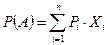C. Никогда не может произойти в результате данного опыта.

D. никогда не может произойти, если произошло событие А.

E. никогда не происходит, если число испытаний невелико.

 

З А Д А Н И Е № 9

Совместными называются события

A. которые наступают одновременно и образуют полную группу событий.

B. которые могут наступать одновременно в результате данного испытания.

C. которые образуют полную группу событий.

D. А и В, при этом событие А наступает, если произошло событие В.

E. которые равновероятны и образуют полную группу событий.

 

З А Д А Н И Е № 10

Несовместные называются события,

A. которые имеют неодинаковые вероятности появления.

B. вероятность которых равна нулю.

C. которые никогда не могут наступать одновременно в результате данного опыта.

D. для которых вероятность события А не изменяется при появлении события В.

E. которые никогда не могут произойти.

 

З А Д А Н И Е № 11

Зависимыми называются события А и В, если

A. Они имеют неодинаковые вероятности появления.

B. Вероятность наступления события В изменяется в зависимости от того, произошло ли событие А.

C. Они никогда не могут наступать одновременно в результате данного опыта.

D. Они могут наступать одновременно в результате данного испытания.

E. Они противоположны друг другу.

 

З А Д А Н И Е № 12

Независимыми называются события А и В, если

A. они противоположны друг другу;

B. они никогда не могут наступать одновременно в результате данного опыта;

C. вероятность наступления события В не изменяется в зависимости от того, произошло ли событие А.

D. вероятность их одновременного наступления равна нулю.

E. событие А не наступает в том случае, когда первым произошло событие В.

 

З А Д А Н И Е № 13

Чему равна сумма вероятностей противоположных событий?

A. 1

B. 0

C. 0,5

D. 0,7

E. 0,3

 

З А Д А Н И Е № 14

Теорема полной вероятности применяется в тех случаях, когда необходимо рассчитать

A. вероятность гипотезы при условии, что событие уже произошло;

B. вероятность события, которое может произойти с одной из гипотез, образующих полную систему;

C. вероятность одной их гипотез, входящих в полную группу событий.

D. вероятность события при условии, что одна из гипотез уже реализовалась.

 

З А Д А Н И Е № 15

Полную группу несовместных событий образуют события А₁, А₂,…,А_n

A. которые наступили в результате проведения испытаний.

B. которые являются совместными и равновозможными.

C. которые несовместны и в результате каждого испытания появляется только одно из этих событий.

D. вероятность которых одинакова.

E. которые являются зависимыми и достоверными.

 

З А Д А Н И Е № 16

Для полной группы событий характерно:

A.

B.

C.

D.

E.

 

З А Д А Н И Е № 17

Классическое определение вероятности случайного события формулируется так:

Вероятностью события А называется

A. предел, к которому стремится отношение относительной частоты к общему числу опытов, при количестве опытов, стремящемся к бесконечности.

B. отношение числа исходов, благоприятствующих событию А, к общему числу равновозможных исходов, образующих полную группу.

C. отношение относительной частоты событий, благоприятствующих опыту, к общему числу испытаний.

D. отношение благоприятствующих случаев к общему числу равновозможных совместных событий.

E. отношение общего числа исходов, к числу благоприятствующих событию А.

 

 

З А Д А Н И Е № 18

Статистическое определение вероятности формулируется так:

Вероятность – это

A. отношение относительной частоты событий, благоприятствующих опыту, к общему числу испытаний

B. предел, к которому стремится относительная частота встречаемости событий при неограниченном увеличении числа испытаний;

C. отношение благоприятствующих случаев к общему числу равновозможных совместных событий;

D. отношение числа исходов, благоприятствующих событию А, к общему числу равновозможных исходов, образующих полную группу.

E. отношение общего числа исходов, к числу благоприятствующих событию А.

 

 

З А Д А Н И Е № 19

Условная вероятность – это вероятность

A. совместного появления зависимых событий.

B. события В при условии, что событие А ему противоположно.